carl Namespace Reference

carl is the main namespace for the library. More...

Namespaces
	benchmarks
	checkpoints
	constraint
	constraints
	contractor
	convert_poly
	convert_ran
	covering
	detail
	detail_derivative
	detail_sign_variations
	dtl
	formula
	formula_to_cnf
	gcd_detail
	helper
	io
	logging
	Contains a custom logging facility.
	model
	parser
	poly_helper
	Helpers due to the shortcomings of libpoly's C++ API.
	pool
	ran
	resultant_debug
	roots
	settings
	statistics
	tree_detail
	vs

Data Structures
class	BasicConstraint
	Represent a polynomial (in)equality against zero. More...
class	CArLConverter
class	ConvertTo
class	ConvertFrom
class	GiNaCConversion
class	ToGiNaC
class	FromGiNaC
class	Variable
	A Variable represents an algebraic variable that can be used throughout carl. More...
class	VariablePool
	This class generates new variables and stores human-readable names for them. More...
class	variable_type_filter
class	carlVariables
class	MultivariateRoot
class	VariableAssignment
class	VariableComparison
	Represent a sum type/variant of an (in)equality between a variable on the left-hand side and multivariateRoot or algebraic real on the right-hand side. More...
struct	DivisionLookupResult
	The result of. More...
struct	UpdateFnct
struct	DefaultBuchbergerSettings
	Standard settings used if the Buchberger object is not instantiated with another template parameter. More...
class	Buchberger
	Gebauer and Moeller style implementation of the Buchberger algorithm. More...
class	BuchbergerStats
	A little class for gathering statistics about the Buchberger algorithm calls. More...
class	CriticalPairConfiguration
class	CriticalPairs
	A data structure to store all the SPolynomial pairs which have to be checked. More...
class	CriticalPairsEntry
	A list of SPol pairs which have to be checked by the Buchberger algorithm. More...
struct	SPolPair
	Basic spol-pair. More...
struct	SPolPairCompare
class	AbstractGBProcedure
class	GBProcedure
	A general class for Groebner Basis calculation. More...
struct	UpdateFnc
struct	StdAdding
struct	RadicalAwareAdding
struct	RealRadicalAwareAdding
class	IdealDatastructureVector
class	Ideal
class	ReductorConfiguration
	Class with the settings for the reduction algorithm. More...
class	Reductor
	A dedicated algorithm for calculating the remainder of a polynomial modulo a set of other polynomials. More...
class	ReductorEntry
	An entry in the reduction polynomial. More...
class	Interval
	The class which contains the interval arithmetic including trigonometric functions. More...
struct	is_interval_type< carl::Interval< Number > >
struct	is_interval_type< const carl::Interval< Number > >
struct	policies
	Struct which holds the rounding and checking policies required for boost interval. More...
struct	policies< double, Interval >
	Template specialization for rounding and checking policies for native double. More...
struct	LowerBound
struct	UpperBound
struct	is_number_type< Interval< T > >
struct	checking
struct	rounding
struct	is_interval_type
	States whether a given type is an Interval. More...
class	VarSolutionFormula
class	Contraction
class	SimpleNewton
struct	is_integer_type< cln::cl_I >
	States that cln::cl_I has the trait is_integer_type . More...
struct	is_rational_type< cln::cl_RA >
	States that cln::cl_RA has the trait is_rational_type . More...
struct	IntegralType< cln::cl_I >
	States that IntegralType of cln::cl_I is cln::cl_I . More...
struct	IntegralType< cln::cl_RA >
	States that IntegralType of cln::cl_RA is cln::cl_I . More...
class	FLOAT_T
	Templated wrapper class which allows universal usage of different IEEE 754 implementations. More...
struct	FloatConv
	Struct which holds the conversion operator for any two instanciations of FLOAT_T with different underlying floating point implementations. More...
struct	convRnd
struct	IntegralType< carl::FLOAT_T< F > >
struct	is_rational_type< FLOAT_T< C > >
struct	is_float_type< carl::FLOAT_T< C > >
struct	is_integer_type< mpz_class >
	States that mpz_class has the trait is_integer_type . More...
struct	is_rational_type< mpq_class >
	States that mpq_class has the trait is_rational_type . More...
struct	IntegralType< mpq_class >
	States that IntegralType of mpq_class is mpz_class . More...
struct	IntegralType< mpz_class >
	States that IntegralType of mpz_class is mpz_class . More...
struct	EEA
	Extended euclidean algorithm for numbers. More...
struct	is_subset_of_integers_type< signed char >
	States that signed char has the trait is_subset_of_integers_type . More...
struct	is_subset_of_integers_type< short int >
	States that short int has the trait is_subset_of_integers_type . More...
struct	is_subset_of_integers_type< int >
	States that int has the trait is_subset_of_integers_type . More...
struct	is_subset_of_integers_type< long int >
	States that long int has the trait is_subset_of_integers_type . More...
struct	is_subset_of_integers_type< long long int >
	States that long long int has the trait is_subset_of_integers_type . More...
struct	is_subset_of_integers_type< unsigned char >
	States that unsigned char has the trait is_subset_of_integers_type . More...
struct	is_subset_of_integers_type< unsigned short int >
	States that unsigned short int has the trait is_subset_of_integers_type . More...
struct	is_subset_of_integers_type< unsigned int >
	States that unsigned int has the trait is_subset_of_integers_type . More...
struct	is_subset_of_integers_type< unsigned long int >
	States that unsigned long int has the trait is_subset_of_integers_type . More...
struct	is_subset_of_integers_type< unsigned long long int >
	States that unsigned long long int has the trait is_subset_of_integers_type . More...
struct	IntegralType< float >
	States that IntegralType of float is sint . More...
struct	IntegralType< double >
	States that IntegralType of double is sint . More...
struct	IntegralType< long double >
	States that IntegralType of long double is sint . More...
struct	constant_zero
struct	constant_one
class	FactorizationFactory
	This class provides a cached factorization for numbers. More...
class	FactorizationFactory< uint >
	This class provides a cached prime factorization for std::size_t. More...
struct	IntegerPairCompare
class	GaloisField
	A finite field. More...
class	GaloisFieldManager
class	GFNumber
	Galois Field numbers, i.e. More...
class	PrimeFactory
	This class provides a convenient way to enumerate primes. More...
struct	remove_all
struct	remove_all< T, T >
struct	has_subtype
	This template is designed to provide types that are related to other types. More...
class	UnivariatePolynomial
	This class represents a univariate polynomial with coefficients of an arbitrary type. More...
class	MultivariatePolynomial
	The general-purpose multivariate polynomial class. More...
struct	is_rational_type
	States if a type is a rational type. More...
struct	is_subset_of_rationals_type
	States if a type represents a subset of all rationals and the representation is similar to a rational. More...
struct	is_field_type
	States if a type is a field. More...
struct	is_field_type< GFNumber< C > >
	States that a Gallois field is a field. More...
struct	is_finite_type
	States if a type represents only a finite domain. More...
struct	is_finite_type< GFNumber< C > >
	Type trait is_finite_type_domain. More...
struct	is_float_type
	States if a type is a floating point type. More...
struct	is_integer_type
	States if a type is an integer type. More...
struct	is_subset_of_integers_type
	States if a type represents a subset of all integers. More...
struct	is_number_type
	States if a type is a number type. More...
struct	is_number_type< GFNumber< C > >
struct	characteristic
	Type trait for the characteristic of the given field (template argument). More...
struct	IntegralType
	Gives the corresponding integral type. More...
struct	IntegralType< GFNumber< C > >
struct	UnderlyingNumberType
	Gives the underlying number type of a complex object. More...
class	PreventConversion
class	Context
class	ContextPolynomial
struct	needs_context_type< ContextPolynomial< Coeff, Ordering, Policies > >
struct	is_polynomial_type< ContextPolynomial< Coeff, Ordering, Policies > >
struct	is_polynomial_type
struct	needs_cache_type
struct	needs_context_type
struct	is_factorized_type
struct	Chebyshev
	Implements a generator for Chebyshev polynomials. More...
struct	DivisionResult
	A strongly typed pair encoding the result of a division, being a quotient and a remainder. More...
class	EZGCD
	Extended Zassenhaus algorithm for multivariate GCD calculation. More...
class	MultivariateHorner
struct	strategy
class	DiophantineEquations
	Includes the algorithms 6.2 and 6.3 from the book Algorithms for Computer Algebra by Geddes, Czaper, Labahn. More...
class	MultivariateHensel
class	TaylorExpansion
class	Monomial
	The general-purpose monomials. More...
struct	hashLess
struct	hashEqual
struct	MonomialComparator
	A class for term orderings. More...
class	MonomialPool
struct	is_polynomial_type< carl::MultivariatePolynomial< T, O, P > >
struct	UnderlyingNumberType< MultivariatePolynomial< C, O, P > >
	States that UnderlyingNumberType of MultivariatePolynomial<C,O,P> is UnderlyingNumberType<C>::type. More...
struct	NoAllocator
struct	NoReasons
struct	BVReasons
struct	StdMultivariatePolynomialPolicies
	The default policy for polynomials. More...
class	Term
	Represents a single term, that is a numeric coefficient and a monomial. More...
class	TermAdditionManager
class	IntRepRealAlgebraicNumber
struct	is_polynomial_type< carl::UnivariatePolynomial< T > >
struct	UnderlyingNumberType< UnivariatePolynomial< C > >
	States that UnderlyingNumberType of UnivariatePolynomial<T> is UnderlyingNumberType<C>::type. More...
class	VarInfo
class	VarsInfo
struct	is_ran_type
class	RealRootsResult
struct	is_ran_type< IntRepRealAlgebraicNumber< Number > >
struct	RealAlgebraicNumberThom
struct	is_ran_type< RealAlgebraicNumberThom< Number > >
class	SignCondition
class	SignDetermination
class	GroebnerBase
struct	BaseRepresentation
class	MultiplicationTable
class	TarskiQueryManager
class	ThomEncoding
class	RealAlgebraicNumber
class	SqrtEx
struct	CompileInfo
	Compile time generated structure holding information about compiler and system version. More...
struct	CMakeOptionPrinter
class	Bitset
	This class is a simple wrapper around boost::dynamic_bitset. More...
class	BitVector
class	tree
	This class represents a tree. More...
class	CompactTree
	This class packs a complete binary tree in a vector. More...
class	Heap
	A heap priority queue. More...
class	Timer
	This classes provides an easy way to obtain the current number of milliseconds that the program has been running. More...
class	Cache
class	IDPool
class	Singleton
	Base class that implements a singleton. More...
struct	overloaded
struct	dependent_bool_type
struct	any
	Meta-logical disjunction. More...
struct	any< Head, Tail... >
struct	all
	Meta-logical conjunction. More...
struct	all< Head, Tail... >
struct	Void
struct	is_instantiation_of
struct	is_instantiation_of< Template, Template< Args... > >
struct	hash_inserter
	Utility functor to hash a sequence of object using an output iterator. More...
struct	mpl_unique
struct	mpl_concatenate_impl
struct	mpl_concatenate_impl< 1, Front, Tail... >
struct	mpl_concatenate
struct	mpl_variant_of_impl
struct	mpl_variant_of_impl< true, Vector, Unpacked... >
struct	mpl_variant_of
struct	equal_to
	Alternative specialization of std::equal_to for pointer types. More...
struct	equal_to< T *, mayBeNull >
struct	equal_to< std::shared_ptr< T >, mayBeNull >
struct	not_equal_to
struct	not_equal_to< T *, mayBeNull >
struct	not_equal_to< std::shared_ptr< T >, mayBeNull >
struct	less
	Alternative specialization of std::less for pointer types. More...
struct	less< T *, mayBeNull >
struct	less< std::shared_ptr< T >, mayBeNull >
struct	greater
struct	greater< T *, mayBeNull >
struct	greater< std::shared_ptr< T >, mayBeNull >
struct	hash
	Alternative specialization of std::hash for pointer types. More...
struct	hash< T *, mayBeNull >
struct	hash< std::shared_ptr< T >, mayBeNull >
class	tuple_convert
class	tuple_convert< Converter, Information, Out >
struct	is_from_variant
struct	convertible_to_variant
class	FactorizedPolynomial
struct	needs_cache_type< FactorizedPolynomial< P > >
struct	is_factorized_type< FactorizedPolynomial< P > >
class	Factorization
class	PolynomialFactorizationPair
class	RationalFunction
class	Constraint
	Represent a polynomial (in)equality against zero. More...
struct	CachedConstraintContent
class	BVConstraint
class	BVConstraintPool
class	BVTerm
struct	BVUnaryContent
struct	BVBinaryContent
struct	BVExtractContent
struct	BVTermContent
class	BVTermPool
class	BVValue
class	BVVariable
	Represent a BitVector-Variable. More...
class	Pool
class	Condition
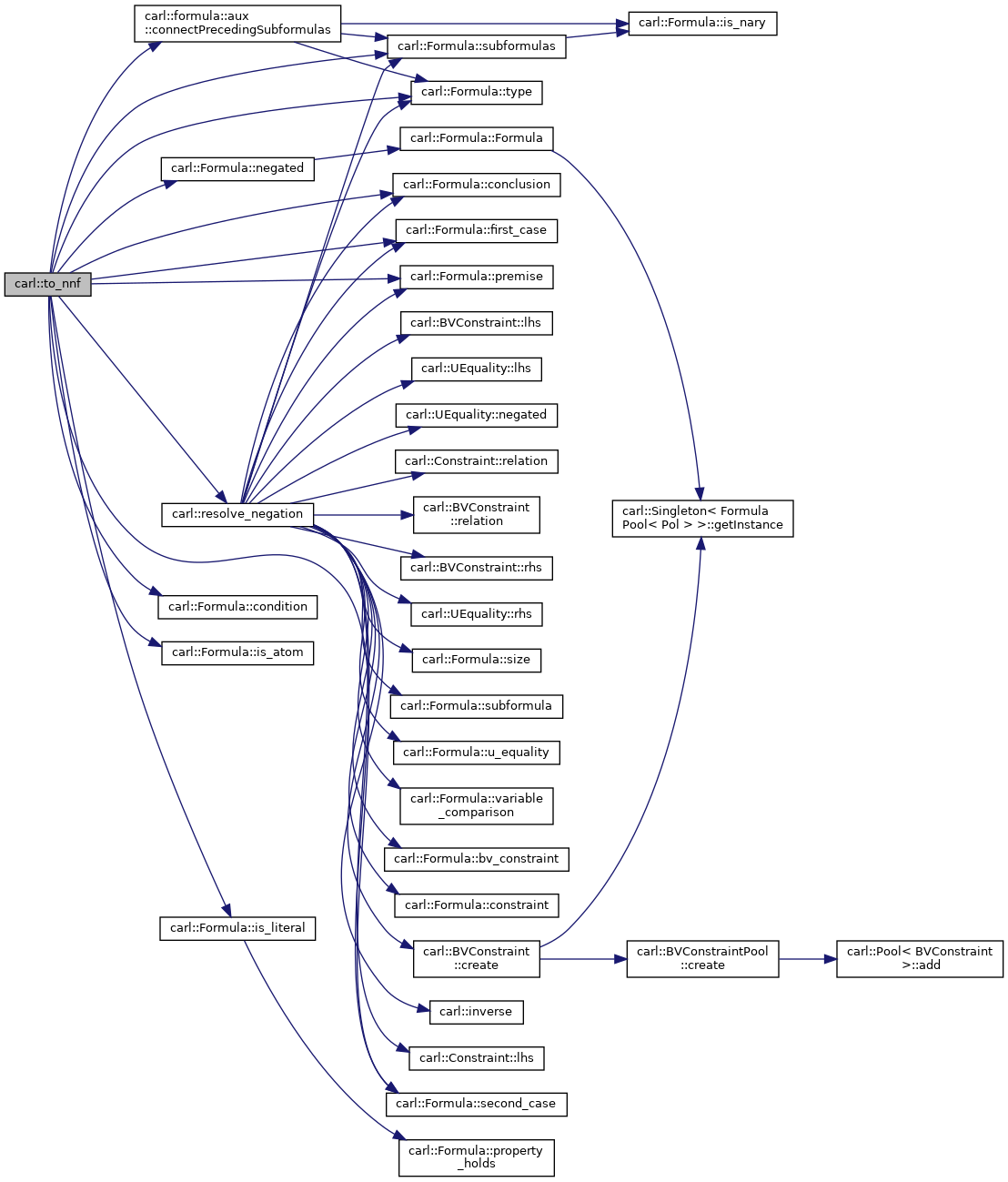
class	Formula
	Represent an SMT formula, which can be an atom for some background theory or a boolean combination of (sub)formulas. More...
class	FormulaPool
struct	QuantifierContent
	Stores the variables and the formula bound by a quantifier. More...
class	FormulaContent
class	Model
	Represent a collection of assignments/mappings from variables to values. More...
class	ModelFormulaSubstitution
class	ModelMVRootSubstitution
class	ModelPolynomialSubstitution
class	ModelSubstitution
	Represent a expression for a ModelValue with variables as placeholders, where the final expression's value depends on the bindings/values of these variables. More...
class	ModelValue
	Represent a sum type/variant over the different kinds of values that can be assigned to the different kinds of variables that exist in CARL and to use them in a more uniform way, e.g. More...
struct	InfinityValue
	This class represents infinity or minus infinity, depending on its flag positive. More...
class	ModelVariable
	Represent a sum type/variant over the different kinds of variables that exist in CARL to use them in a more uniform way, e.g. More...
class	ModelConditionalSubstitution
class	Sort
	Implements a sort (for defining types of variables and functions). More...
struct	SortContent
	The actual content of a sort. More...
class	SortManager
	Implements a manager for sorts, containing the actual contents of these sort and allocating their ids. More...
class	SortValue
	Implements a sort value, being a value of the uninterpreted domain specified by this sort. More...
class	SortValueManager
	Implements a manager for sort values, containing the actual contents of these sort and allocating their ids. More...
class	UEquality
	Implements an uninterpreted equality, that is an equality of either two uninterpreted function instances, two uninterpreted variables, or an uninterpreted function instance and an uninterpreted variable. More...
class	UFInstance
	Implements an uninterpreted function instance. More...
class	UFInstanceContent
	The actual content of an uninterpreted function instance. More...
class	UFInstanceManager
	Implements a manager for uninterpreted function instances, containing their actual contents and allocating their ids. More...
class	UFContent
	The actual content of an uninterpreted function instance. More...
class	UFManager
	Implements a manager for uninterpreted functions, containing their actual contents and allocating their ids. More...
class	UFModel
	Implements a sort value, being a value of the uninterpreted domain specified by this sort. More...
class	UninterpretedFunction
	Implements an uninterpreted function. More...
class	UTerm
	Implements an uninterpreted term, that is either an uninterpreted variable or an uninterpreted function instance. More...
class	UVariable
	Implements an uninterpreted variable. More...

Typedefs
template<typename T >
using	Assignment = std::map< Variable, T >
template<typename T >
using	OrderedAssignment = std::vector< std::pair< Variable, T > >
using	Variables = std::set< Variable >
template<typename Pol >
using	Factors = std::map< Pol, uint >
template<typename Poly >
using	EncodingCache = std::map< MultivariateRoot< Poly >, std::pair< std::vector< BasicConstraint< Poly > >, Variable > >
typedef CriticalPairs< Heap, CriticalPairConfiguration< GrLexOrdering > >	CritPairs
using	precision_t = std::size_t
using	uint = std::uint64_t
using	sint = std::int64_t
template<typename C >
using	IntegralTypeIfDifferent = typename std::enable_if<!std::is_same< C, typename IntegralType< C >::type >::value, typename IntegralType< C >::type >::type
using	exponent = std::size_t
	Type of an exponent. More...
using	MonomialOrderingFunction = CompareResult(*)(const Monomial::Arg &, const Monomial::Arg &)
using	LexOrdering = MonomialComparator< Monomial::compareLexical, false >
using	GrLexOrdering = MonomialComparator< Monomial::compareGradedLexical, true >
template<typename Coefficient >
using	UnivariatePolynomialPtr = std::shared_ptr< UnivariatePolynomial< Coefficient > >
template<typename Coefficient >
using	FactorMap = std::map< UnivariatePolynomial< Coefficient >, uint >
template<typename Coeff >
using	CoeffMatrix = Eigen::Matrix< Coeff, Eigen::Dynamic, Eigen::Dynamic >
template<typename T , class I >
using	TypeInfoPair = std::pair< T *, I >
template<bool If, typename Then , typename Else >
using	Conditional = typename std::conditional< If, Then, Else >::type
template<bool B, typename... T>
using	Bool = typename dependent_bool_type< B, T... >::type
template<typename T >
using	Not = Bool<!T::value >
	Meta-logical negation. More...
template<typename... Condition>
using	EnableIf = typename std::enable_if< all< Condition... >::value, dtl::enabled >::type
template<typename... Condition>
using	DisableIf = typename std::enable_if< Not< any< Condition... > >::value, dtl::enabled >::type
template<bool Condition>
using	EnableIfBool = typename std::enable_if< Condition, dtl::enabled >::type
template<typename T >
using	pointerEqual = carl::equal_to< const T *, false >
template<typename T >
using	pointerEqualWithNull = carl::equal_to< const T *, true >
template<typename T >
using	sharedPointerEqual = carl::equal_to< std::shared_ptr< const T >, false >
template<typename T >
using	sharedPointerEqualWithNull = carl::equal_to< std::shared_ptr< const T >, true >
template<typename T >
using	pointerLess = carl::less< const T *, false >
template<typename T >
using	pointerLessWithNull = carl::less< const T *, true >
template<typename T >
using	sharedPointerLess = carl::less< std::shared_ptr< const T > *, false >
template<typename T >
using	sharedPointerLessWithNull = carl::less< std::shared_ptr< const T >, true >
template<typename T >
using	pointerHash = carl::hash< T *, false >
template<typename T >
using	pointerHashWithNull = carl::hash< T *, true >
template<typename T >
using	sharedPointerHash = carl::hash< std::shared_ptr< const T > *, false >
template<typename T >
using	sharedPointerHashWithNull = carl::hash< std::shared_ptr< const T > *, true >
template<typename T >
using	PointerSet = std::set< const T *, pointerLess< T > >
template<typename T >
using	PointerMultiSet = std::multiset< const T *, pointerLess< T > >
template<typename T1 , typename T2 >
using	PointerMap = std::map< const T1 *, T2, pointerLess< T1 > >
template<typename T >
using	SharedPointerSet = std::set< std::shared_ptr< const T >, sharedPointerLess< T > >
template<typename T >
using	SharedPointerMultiSet = std::multiset< std::shared_ptr< const T >, sharedPointerLess< T > >
template<typename T1 , typename T2 >
using	SharedPointerMap = std::map< std::shared_ptr< const T1 >, T2, sharedPointerLess< T1 > >
template<typename T >
using	FastSet = std::unordered_set< T, std::hash< T > >
template<typename T1 , typename T2 >
using	FastMap = std::unordered_map< T1, T2, std::hash< T1 > >
template<typename T >
using	FastPointerSet = std::unordered_set< const T *, pointerHash< T >, pointerEqual< T > >
template<typename T1 , typename T2 >
using	FastPointerMap = std::unordered_map< const T1 *, T2, pointerHash< T1 >, pointerEqual< T1 > >
template<typename T >
using	FastSharedPointerSet = std::unordered_set< std::shared_ptr< const T >, sharedPointerHash< T >, sharedPointerEqual< T > >
template<typename T1 , typename T2 >
using	FastSharedPointerMap = std::unordered_map< std::shared_ptr< const T1 >, T2, sharedPointerHash< T1 >, sharedPointerEqual< T1 > >
template<typename T >
using	FastPointerSetB = std::unordered_set< const T *, pointerHashWithNull< T >, pointerEqualWithNull< T > >
template<typename T1 , typename T2 >
using	FastPointerMapB = std::unordered_map< const T1 *, T2, pointerHashWithNull< T1 >, pointerEqualWithNull< T1 > >
template<typename T >
using	FastSharedPointerSetB = std::unordered_set< std::shared_ptr< const T >, sharedPointerHashWithNull< T >, pointerEqualWithNull< T > >
template<typename T1 , typename T2 >
using	FastSharedPointerMapB = std::unordered_map< std::shared_ptr< const T1 >, T2, sharedPointerHashWithNull< T1 >, pointerEqualWithNull< T1 > >
template<typename P >
using	Coeff = typename UnderlyingNumberType< P >::type
template<typename Poly >
using	Constraints = std::set< Constraint< Poly >, carl::less< Constraint< Poly >, false > >
template<typename Pol >
using	ConstraintPool = pool::Pool< CachedConstraintContent< Pol > >
template<typename Poly >
using	Formulas = std::vector< Formula< Poly > >
template<typename Poly >
using	FormulaSet = std::set< Formula< Poly > >
template<typename Poly >
using	FormulasMulti = std::multiset< Formula< Poly > >
template<typename Pol >
using	ConstraintBounds = FastMap< Pol, std::map< typename Pol::NumberType, std::pair< Relation, Formula< Pol > >> >
	A map from formula pointers to a map of rationals to a pair of a constraint relation and a formula pointer. (internally used) More...
using	QuantifierPrefix = std::vector< std::pair< Quantifier, carl::Variable > >
template<typename Rational , typename Poly >
using	ModelSubstitutionPtr = std::unique_ptr< ModelSubstitution< Rational, Poly > >

Enumerations
enum class	CompareResult { LESS = -1 , EQUAL = 0 , GREATER = 1 }
enum class	Relation {   EQ = 0 , NEQ = 1 , LESS = 2 , LEQ = 4 ,   GREATER = 3 , GEQ = 5 }
enum class	Sign { NEGATIVE = -1 , ZERO = 0 , POSITIVE = 1 }
	This class represents the sign of a number . More...
enum class	VariableType {   VT_BOOL = 0 , VT_REAL = 1 , VT_INT = 2 , VT_UNINTERPRETED = 3 ,   VT_BITVECTOR = 4 , MIN_TYPE = VT_BOOL , MAX_TYPE = VT_BITVECTOR , TYPE_SIZE = MAX_TYPE - MIN_TYPE + 1 }
	Several types of variables are supported. More...
enum class	BoundType { STRICT = 0 , WEAK = 1 , INFTY = 2 }
enum	Str2Double_Error { FLOAT_SUCCESS , FLOAT_OVERFLOW , FLOAT_UNDERFLOW , FLOAT_INCONVERTIBLE }
enum class	CARL_RND : int {   N =0 , Z =1 , U =2 , D =3 ,   A =4 }
enum class	Definiteness {   NEGATIVE = 0 , NEGATIVE_SEMI = 1 , NON = 2 , POSITIVE_SEMI = 3 ,   POSITIVE = 4 }
	Regarding a polynomial as a function , its definiteness gives information about the codomain . More...
enum	variableSelectionHeurisics { GREEDY_I = 0 , GREEDY_Is = 1 , GREEDY_II = 2 , GREEDY_IIs = 3 }
enum class	SubresultantStrategy { Generic , Lazard , Ducos , Default = Lazard }
enum class	PolynomialComparisonOrder { CauchyBound , LowDegree , Memory , Default = LowDegree }
enum	ThomComparisonResult {   LESS , LESS = -1 , LESS = 2 , EQUAL ,   EQUAL = 0 , GREATER , GREATER = 1 , GREATER = 3 }
enum class	BVCompareRelation : unsigned {   EQ , NEQ , ULT , ULE ,   UGT , UGE , SLT , SLE ,   SGT , SGE }
enum class	BVTermType {   CONSTANT , VARIABLE , CONCAT , EXTRACT ,   NOT , NEG , AND , OR ,   XOR , NAND , NOR , XNOR ,   ADD , SUB , MUL , DIV_U ,   DIV_S , MOD_U , MOD_S1 , MOD_S2 ,   EQ , LSHIFT , RSHIFT_LOGIC , RSHIFT_ARITH ,   LROTATE , RROTATE , EXT_U , EXT_S ,   REPEAT }
enum	FormulaType {   ITE , EXISTS , FORALL , TRUE ,   FALSE , BOOL , NOT , NOT ,   IMPLIES , AND , AND , OR ,   OR , XOR , XOR , IFF ,   CONSTRAINT , VARCOMPARE , VARASSIGN , BITVECTOR ,   UEQ }
	Represent the type of a formula to allow faster/specialized processing. More...
enum class	Quantifier { EXISTS , FORALL , FREE }
enum class	Logic {   QF_BV , QF_IDL , QF_LIA , QF_LIRA ,   QF_LRA , QF_NIA , QF_NIRA , QF_NRA ,   QF_PB , QF_RDL , QF_UF , NRA ,   LRA , UNDEFINED }

Functions
template<typename P >
bool	operator== (const BasicConstraint< P > &lhs, const BasicConstraint< P > &rhs)
template<typename P >
bool	operator!= (const BasicConstraint< P > &lhs, const BasicConstraint< P > &rhs)
template<typename P >
bool	operator< (const BasicConstraint< P > &lhs, const BasicConstraint< P > &rhs)
template<typename P >
bool	operator<= (const BasicConstraint< P > &lhs, const BasicConstraint< P > &rhs)
template<typename P >
bool	operator> (const BasicConstraint< P > &lhs, const BasicConstraint< P > &rhs)
template<typename P >
bool	operator>= (const BasicConstraint< P > &lhs, const BasicConstraint< P > &rhs)
template<typename Pol >
void	variables (const BasicConstraint< Pol > &c, carlVariables &vars)
template<typename Poly >
std::ostream &	operator<< (std::ostream &os, const BasicConstraint< Poly > &c)
	Prints the given constraint on the given stream. More...
template<typename Pol >
bool	is_bound (const BasicConstraint< Pol > &constr)
template<typename Pol >
bool	is_lower_bound (const BasicConstraint< Pol > &constr)
template<typename Pol >
bool	is_upper_bound (const BasicConstraint< Pol > &constr)
template<typename Pol >
signed	compare (const BasicConstraint< Pol > &_constraintA, const BasicConstraint< Pol > &_constraintB)
	Compares _constraintA with _constraintB. More...
template<typename Poly >
std::size_t	complexity (const BasicConstraint< Poly > &c)
template<typename ToPoly , typename FromPoly , typename = std::enable_if_t<needs_context_type<ToPoly>::value>>
BasicConstraint< ToPoly >	convert (const typename ToPoly::ContextType &context, const BasicConstraint< FromPoly > &c)
template<typename ToPoly , typename FromPoly , typename = std::enable_if_t<!needs_context_type<ToPoly>::value>>
BasicConstraint< ToPoly >	convert (const BasicConstraint< FromPoly > &c)
template<typename Number , typename Poly , typename = std::enable_if_t<is_number_type<Number>::value>>
bool	evaluate (const BasicConstraint< Poly > &c, const Assignment< Number > &m)
template<typename Pol >
unsigned	satisfied_by (const BasicConstraint< Pol > &c, const Assignment< typename Pol::NumberType > &_assignment)
	Checks whether the given assignment satisfies this constraint. More...
template<typename Number , typename Poly >
boost::tribool	evaluate (const BasicConstraint< Poly > &c, const Assignment< Interval< Number >> &map)
template<typename Pol >
static unsigned	consistent_with (const BasicConstraint< Pol > &c, const Assignment< Interval< double >> &_solutionInterval)
	Checks whether this constraint is consistent with the given assignment from the its variables to interval domains. More...
template<typename Pol >
static unsigned	consistent_with (const BasicConstraint< Pol > &c, const Assignment< Interval< double >> &_solutionInterval, Relation &_stricterRelation)
	Checks whether this constraint is consistent with the given assignment from the its variables to interval domains. More...
template<typename Pol >
std::optional< std::pair< Variable, Pol > >	get_substitution (const BasicConstraint< Pol > &c, bool _negated=false, Variable _exclude=carl::Variable::NO_VARIABLE, std::optional< VarsInfo< Pol >> var_info=std::nullopt)
	If this constraint represents a substitution (equation, where at least one variable occurs only linearly), this method detects a (there could be various possibilities) corresponding substitution variable and term. More...
template<typename Pol >
std::optional< std::pair< Variable, typename Pol::NumberType > >	get_assignment (const BasicConstraint< Pol > &c)
std::ostream &	operator<< (std::ostream &os, CompareResult cr)
std::ostream &	operator<< (std::ostream &os, const Relation &r)
Relation	inverse (Relation r)
	Inverts the given relation symbol. More...
Relation	turn_around (Relation r)
	Turns around the given relation symbol, in the sense that LESS (LEQ) and GREATER (GEQ) are swapped. More...
std::string	toString (Relation r)
bool	is_strict (Relation r)
bool	is_weak (Relation r)
bool	evaluate (Sign s, Relation r)
template<typename T >
bool	evaluate (const T &t, Relation r)
template<typename T1 , typename T2 >
bool	evaluate (const T1 &lhs, Relation r, const T2 &rhs)
std::ostream &	operator<< (std::ostream &os, const Sign &sign)
template<typename Number >
Sign	sgn (const Number &n)
	Obtain the sign of the given number. More...
template<typename InputIterator >
std::size_t	sign_variations (InputIterator begin, InputIterator end)
	Counts the number of sign variations in the given object range. More...
template<typename InputIterator , typename Function >
std::size_t	sign_variations (InputIterator begin, InputIterator end, const Function &f)
	Counts the number of sign variations in the given object range. More...
std::ostream &	operator<< (std::ostream &os, const VariableType &t)
	Streaming operator for VariableType. More...
std::ostream &	operator<< (std::ostream &os, Variable rhs)
	Streaming operator for Variable. More...
Variable	fresh_variable (VariableType vt) noexcept
Variable	fresh_variable (const std::string &name, VariableType vt)
Variable	fresh_bitvector_variable () noexcept
Variable	fresh_bitvector_variable (const std::string &name)
Variable	fresh_boolean_variable () noexcept
Variable	fresh_boolean_variable (const std::string &name)
Variable	fresh_real_variable () noexcept
Variable	fresh_real_variable (const std::string &name)
Variable	fresh_integer_variable () noexcept
Variable	fresh_integer_variable (const std::string &name)
Variable	fresh_uninterpreted_variable () noexcept
Variable	fresh_uninterpreted_variable (const std::string &name)
void	swap (Variable &lhs, Variable &rhs)
bool	operator== (const carlVariables &lhs, const carlVariables &rhs)
std::ostream &	operator<< (std::ostream &os, const carlVariables &vars)
template<typename T >
carlVariables	variables (const T &t)
	Return the variables as collected by the methods above. More...
template<typename T >
carlVariables	boolean_variables (const T &t)
template<typename T >
carlVariables	integer_variables (const T &t)
template<typename T >
carlVariables	real_variables (const T &t)
template<typename T >
carlVariables	arithmetic_variables (const T &t)
template<typename T >
carlVariables	bitvector_variables (const T &t)
template<typename T >
carlVariables	uninterpreted_variables (const T &t)
template<typename ToPoly , typename FromPoly , typename = std::enable_if_t<needs_context_type<ToPoly>::value>>
VariableComparison< ToPoly >	convert (const typename ToPoly::ContextType &context, const VariableComparison< FromPoly > &c)
template<typename ToPoly , typename FromPoly , typename = std::enable_if_t<!needs_context_type<ToPoly>::value>>
VariableComparison< ToPoly >	convert (const VariableComparison< FromPoly > &c)
template<typename Poly >
void	encode_as_constraints_simple (const MultivariateRoot< Poly > &f, Assignment< typename VariableComparison< Poly >::RAN > ass, Variable var, std::vector< BasicConstraint< Poly >> &out)
template<typename Poly >
void	encode_as_constraints_thom (const MultivariateRoot< Poly > &f, Assignment< typename VariableComparison< Poly >::RAN > ass, Variable var, std::vector< BasicConstraint< Poly >> &out)
template<typename Poly >
std::pair< std::vector< BasicConstraint< Poly > >, Variable >	encode_as_constraints (const MultivariateRoot< Poly > &f, Assignment< typename VariableComparison< Poly >::RAN > ass, EncodingCache< Poly > cache)
template<typename Poly >
std::pair< std::vector< BasicConstraint< Poly > >, BasicConstraint< Poly > >	encode_as_constraints (const VariableComparison< Poly > &f, const Assignment< typename VariableComparison< Poly >::RAN > &ass, EncodingCache< Poly > cache)
template<typename Poly >
bool	operator== (const MultivariateRoot< Poly > &lhs, const MultivariateRoot< Poly > &rhs)
template<typename Poly >
bool	operator< (const MultivariateRoot< Poly > &lhs, const MultivariateRoot< Poly > &rhs)
template<typename P >
std::ostream &	operator<< (std::ostream &os, const MultivariateRoot< P > &mr)
template<typename Poly >
void	variables (const MultivariateRoot< Poly > &mr, carlVariables &vars)
	Add the variables mentioned in underlying polynomial, excluding the root-variable "_z". More...
template<typename Poly >
void	substitute_inplace (MultivariateRoot< Poly > &mr, Variable var, const Poly &poly)
	Create a copy of the underlying polynomial with the given variable replaced by the given polynomial. More...
template<typename Poly >
MultivariateRoot< Poly >	convert_to_mvroot (const typename MultivariateRoot< Poly >::RAN &ran, Variable var)
template<typename Poly >
std::optional< typename MultivariateRoot< Poly >::RAN >	evaluate (const MultivariateRoot< Poly > &mr, const carl::Assignment< typename MultivariateRoot< Poly >::RAN > &m)
	Return the emerging algebraic real after pluggin in a subpoint to replace all variables with algebraic reals that are not the root-variable "_z". More...
template<typename Pol >
void	variables (const VariableAssignment< Pol > &f, carlVariables &vars)
template<typename Poly >
bool	operator== (const VariableAssignment< Poly > &lhs, const VariableAssignment< Poly > &rhs)
template<typename Poly >
bool	operator< (const VariableAssignment< Poly > &lhs, const VariableAssignment< Poly > &rhs)
template<typename Poly >
std::ostream &	operator<< (std::ostream &os, const VariableAssignment< Poly > &va)
template<typename Poly , std::enable_if_t<!needs_context_type< Poly >::value, bool > = true>
std::optional< BasicConstraint< Poly > >	as_constraint (const VariableComparison< Poly > &f)
	Convert this variable comparison "v < root(..)" into a simpler polynomial (in)equality against zero "p(..) < 0" if that is possible. More...
template<typename Poly , std::enable_if_t<!needs_context_type< Poly >::value, bool > = true>
Poly	defining_polynomial (const VariableComparison< Poly > &f)
	Return a polynomial containing the lhs-variable that has a same root for the this lhs-variable as the value that rhs represent, e.g. More...
template<typename Poly >
boost::tribool	evaluate (const VariableComparison< Poly > &f, const Assignment< typename VariableComparison< Poly >::RAN > &a, bool evaluate_non_welldef=false)
template<typename Pol >
void	variables (const VariableComparison< Pol > &f, carlVariables &vars)
template<typename Poly >
bool	operator== (const VariableComparison< Poly > &lhs, const VariableComparison< Poly > &rhs)
template<typename Poly >
bool	operator< (const VariableComparison< Poly > &lhs, const VariableComparison< Poly > &rhs)
template<typename Poly >
std::ostream &	operator<< (std::ostream &os, const VariableComparison< Poly > &vc)
template<class C >
std::ostream &	operator<< (std::ostream &os, const ReductorEntry< C > rhs)
int	init ()
	The routine for initializing the carl library. More...
int	initialize ()
	Method to ensure that upon inclusion, init() is called exactly once. More...
std::ostream &	operator<< (std::ostream &os, BoundType b)
static BoundType	get_weakest_bound_type (BoundType type1, BoundType type2)
static BoundType	get_strictest_bound_type (BoundType type1, BoundType type2)
static BoundType	get_other_bound_type (BoundType type)
template<typename From , typename To , carl::DisableIf< std::is_same< From, To > > = dummy>
Interval< To >	convert (const Interval< From > &i)
template<typename Number >
boost::tribool	evaluate (Interval< Number > interval, Relation relation)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
Interval< Number >	exp (const Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
void	exp_assign (Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
Interval< Number >	log (const Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
void	log_assign (Interval< Number > &i)
template<typename Number >
std::ostream &	operator<< (std::ostream &os, const LowerBound< Number > &lb)
template<typename Number >
std::ostream &	operator<< (std::ostream &os, const UpperBound< Number > &lb)
template<typename Number >
bool	is_integer (const Interval< Number > &n)
template<typename Number >
bool	is_zero (const Interval< Number > &i)
	Check if this interval is a point-interval containing 0. More...
template<typename Number >
bool	is_one (const Interval< Number > &i)
	Check if this interval is a point-interval containing 1. More...
template<typename Number >
Interval< Number >	div (const Interval< Number > &_lhs, const Interval< Number > &_rhs)
	Implements the division which assumes that there is no remainder. More...
template<typename Number >
Interval< Number >	quotient (const Interval< Number > &_lhs, const Interval< Number > &_rhs)
	Implements the division with remainder. More...
template<typename Integer , typename Number >
Integer	to_int (const Interval< Number > &_floatInterval)
	Casts the Interval to an arbitrary integer type which has a constructor for a native int. More...
template<typename Number >
Interval< Number >	abs (const Interval< Number > &_in)
	Method which returns the absolute value of the passed number. More...
template<typename Number >
Interval< Number >	floor (const Interval< Number > &_in)
	Method which returns the next smaller integer of this number or the number itself, if it is already an integer. More...
template<typename Number >
Interval< Number >	ceil (const Interval< Number > &_in)
	Method which returns the next larger integer of the passed number or the number itself, if it is already an integer. More...
template<typename Number >
bool	operator< (const LowerBound< Number > &lhs, const LowerBound< Number > &rhs)
	Operators for LowerBound and UpperBound. More...
template<typename Number >
bool	operator<= (const LowerBound< Number > &lhs, const LowerBound< Number > &rhs)
template<typename Number >
bool	operator< (const UpperBound< Number > &lhs, const LowerBound< Number > &rhs)
template<typename Number >
bool	operator<= (const LowerBound< Number > &lhs, const UpperBound< Number > &rhs)
template<typename Number >
bool	operator< (const UpperBound< Number > &lhs, const UpperBound< Number > &rhs)
template<typename Number >
bool	operator<= (const UpperBound< Number > &lhs, const UpperBound< Number > &rhs)
template<typename Number >
bool	bounds_connect (const UpperBound< Number > &lhs, const LowerBound< Number > &rhs)
	Check whether the two bounds connect, for example as for ...3),[3... More...
template<typename Number >
bool	operator== (const Interval< Number > &lhs, const Interval< Number > &rhs)
	Operator for the comparison of two intervals. More...
template<>
bool	operator== (const Interval< double > &lhs, const Interval< double > &rhs)
template<typename Number >
bool	operator== (const Interval< Number > &lhs, const Number &rhs)
template<typename Number >
bool	operator== (const Number &lhs, const Interval< Number > &rhs)
template<typename Number >
bool	operator!= (const Interval< Number > &lhs, const Interval< Number > &rhs)
	Operator for the comparison of two intervals. More...
template<typename Number >
bool	operator!= (const Interval< Number > &lhs, const Number &rhs)
template<typename Number >
bool	operator!= (const Number &lhs, const Interval< Number > &rhs)
template<typename Number >
bool	operator< (const Interval< Number > &lhs, const Interval< Number > &rhs)
	Operator for the comparison of two intervals. More...
template<typename Number >
bool	operator< (const Interval< Number > &lhs, const Number &rhs)
template<typename Number >
bool	operator< (const Number &lhs, const Interval< Number > &rhs)
template<typename Number >
bool	operator> (const Interval< Number > &lhs, const Interval< Number > &rhs)
	Operator for the comparison of two intervals. More...
template<typename Number >
bool	operator> (const Interval< Number > &lhs, const Number &rhs)
template<typename Number >
bool	operator> (const Number &lhs, const Interval< Number > &rhs)
template<typename Number >
bool	operator<= (const Interval< Number > &lhs, const Interval< Number > &rhs)
	Operator for the comparison of two intervals. More...
template<typename Number >
bool	operator<= (const Interval< Number > &lhs, const Number &rhs)
template<typename Number >
bool	operator<= (const Number &lhs, const Interval< Number > &rhs)
template<typename Number >
bool	operator>= (const Interval< Number > &lhs, const Interval< Number > &rhs)
	Operator for the comparison of two intervals. More...
template<typename Number >
bool	operator>= (const Interval< Number > &lhs, const Number &rhs)
template<typename Number >
bool	operator>= (const Number &lhs, const Interval< Number > &rhs)
template<typename Number >
Interval< Number >	operator+ (const Interval< Number > &lhs, const Interval< Number > &rhs)
	Operator for the addition of two intervals. More...
template<typename Number >
Interval< Number >	operator+ (const Interval< Number > &lhs, const Number &rhs)
	Operator for the addition of an interval and a number. More...
template<typename Number >
Interval< Number >	operator+ (const Number &lhs, const Interval< Number > &rhs)
	Operator for the addition of an interval and a number. More...
template<typename Number >
Interval< Number > &	operator+= (Interval< Number > &lhs, const Interval< Number > &rhs)
	Operator for the addition of an interval and a number with assignment. More...
template<typename Number >
Interval< Number > &	operator+= (Interval< Number > &lhs, const Number &rhs)
	Operator for the addition of an interval and a number with assignment. More...
template<typename Number >
Interval< Number >	operator- (const Interval< Number > &rhs)
	Unary minus. More...
template<typename Number >
Interval< Number >	operator- (const Interval< Number > &lhs, const Interval< Number > &rhs)
	Operator for the subtraction of two intervals. More...
template<typename Number >
Interval< Number >	operator- (const Interval< Number > &lhs, const Number &rhs)
	Operator for the subtraction of an interval and a number. More...
template<typename Number >
Interval< Number >	operator- (const Number &lhs, const Interval< Number > &rhs)
	Operator for the subtraction of an interval and a number. More...
template<typename Number >
Interval< Number > &	operator-= (Interval< Number > &lhs, const Interval< Number > &rhs)
	Operator for the subtraction of two intervals with assignment. More...
template<typename Number >
Interval< Number > &	operator-= (Interval< Number > &lhs, const Number &rhs)
	Operator for the subtraction of an interval and a number with assignment. More...
template<typename Number >
Interval< Number >	operator* (const Interval< Number > &lhs, const Interval< Number > &rhs)
	Operator for the multiplication of two intervals. More...
template<typename Number >
Interval< Number >	operator* (const Interval< Number > &lhs, const Number &rhs)
	Operator for the multiplication of an interval and a number. More...
template<typename Number >
Interval< Number >	operator* (const Number &lhs, const Interval< Number > &rhs)
	Operator for the multiplication of an interval and a number. More...
template<typename Number >
Interval< Number > &	operator*= (Interval< Number > &lhs, const Interval< Number > &rhs)
	Operator for the multiplication of an interval and a number with assignment. More...
template<typename Number >
Interval< Number > &	operator*= (Interval< Number > &lhs, const Number &rhs)
	Operator for the multiplication of an interval and a number with assignment. More...
template<typename Number >
Interval< Number >	operator/ (const Interval< Number > &lhs, const Number &rhs)
	Operator for the division of an interval and a number. More...
template<typename Number >
Interval< Number > &	operator/= (Interval< Number > &lhs, const Number &rhs)
	Operator for the division of an interval and a number with assignment. More...
template<typename Number , typename Integer >
Interval< Number >	pow (const Interval< Number > &i, Integer exp)
template<typename Number , typename Integer >
void	pow_assign (Interval< Number > &i, Integer exp)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
Interval< Number >	sqrt (const Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
void	sqrt_assign (Interval< Number > &i)
template<typename Number >
Number	center (const Interval< Number > &i)
	Returns the center point of the interval. More...
template<typename Number >
Number	sample (const Interval< Number > &i, bool includingBounds=true)
	Searches for some point in this interval, preferably near the midpoint and with a small representation. More...
template<typename Number >
Number	sample_stern_brocot (const Interval< Number > &i, bool includingBounds=true)
	Searches for some point in this interval, preferably near the midpoint and with a small representation. More...
template<typename Number >
Number	sample_left (const Interval< Number > &i)
	Searches for some point in this interval, preferably near the left endpoint and with a small representation. More...
template<typename Number >
Number	sample_right (const Interval< Number > &i)
	Searches for some point in this interval, preferably near the right endpoint and with a small representation. More...
template<typename Number >
Number	sample_zero (const Interval< Number > &i)
	Searches for some point in this interval, preferably near zero and with a small representation. More...
template<typename Number >
Number	sample_infty (const Interval< Number > &i)
	Searches for some point in this interval, preferably far aways from zero and with a small representation. More...
template<typename Number >
bool	set_complement (const Interval< Number > &interval, Interval< Number > &resA, Interval< Number > &resB)
	Calculates the complement in a set-theoretic manner (can result in two distinct intervals). More...
template<typename Number >
bool	set_difference (const Interval< Number > &lhs, const Interval< Number > &rhs, Interval< Number > &resA, Interval< Number > &resB)
	Calculates the difference of two intervals in a set-theoretic manner: lhs \ rhs (can result in two distinct intervals). More...
template<typename Number >
Interval< Number >	set_intersection (const Interval< Number > &lhs, const Interval< Number > &rhs)
	Intersects two intervals in a set-theoretic manner. More...
template<typename Number >
bool	set_have_intersection (const Interval< Number > &lhs, const Interval< Number > &rhs)
template<typename Number >
bool	set_is_proper_subset (const Interval< Number > &lhs, const Interval< Number > &rhs)
	Checks whether lhs is a proper subset of rhs. More...
template<typename Number >
bool	set_is_subset (const Interval< Number > &lhs, const Interval< Number > &rhs)
	Checks whether lhs is a subset of rhs. More...
template<typename Number >
bool	set_symmetric_difference (const Interval< Number > &lhs, const Interval< Number > &rhs, Interval< Number > &resA, Interval< Number > &resB)
	Calculates the symmetric difference of two intervals in a set-theoretic manner (can result in two distinct intervals). More...
template<typename Number >
bool	set_union (const Interval< Number > &lhs, const Interval< Number > &rhs, Interval< Number > &resA, Interval< Number > &resB)
	Computes the union of two intervals (can result in two distinct intervals). More...
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
Interval< Number >	sin (const Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
void	sin_assign (Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
Interval< Number >	cos (const Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
void	cos_assign (Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
Interval< Number >	tan (const Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
void	tan_assign (Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
Interval< Number >	asin (const Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
void	asin_assign (Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
Interval< Number >	acos (const Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
void	acos_assign (Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
Interval< Number >	atan (const Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
void	atan_assign (Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
Interval< Number >	sinh (const Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
void	sinh_assign (Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
Interval< Number >	cosh (const Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
void	cosh_assign (Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
Interval< Number >	tanh (const Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
void	tanh_assign (Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
Interval< Number >	asinh (const Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
void	asinh_assign (Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
Interval< Number >	acosh (const Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
void	acosh_assign (Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
Interval< Number >	atanh (const Interval< Number > &i)
template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>
void	atanh_assign (Interval< Number > &i)
bool	is_zero (const cln::cl_I &n)
bool	is_zero (const cln::cl_RA &n)
bool	is_one (const cln::cl_I &n)
bool	is_one (const cln::cl_RA &n)
bool	is_positive (const cln::cl_I &n)
bool	is_positive (const cln::cl_RA &n)
bool	is_negative (const cln::cl_I &n)
bool	is_negative (const cln::cl_RA &n)
cln::cl_I	get_num (const cln::cl_RA &n)
	Extract the numerator from a fraction. More...
cln::cl_I	get_denom (const cln::cl_RA &n)
	Extract the denominator from a fraction. More...
bool	is_integer (const cln::cl_I &)
	Check if a number is integral. More...
bool	is_integer (const cln::cl_RA &n)
	Check if a fraction is integral. More...
std::size_t	bitsize (const cln::cl_I &n)
	Get the bit size of the representation of a integer. More...
std::size_t	bitsize (const cln::cl_RA &n)
	Get the bit size of the representation of a fraction. More...
double	to_double (const cln::cl_RA &n)
	Converts the given fraction to a double. More...
double	to_double (const cln::cl_I &n)
	Converts the given integer to a double. More...
template<typename Integer >
Integer	to_int (const cln::cl_I &n)
template<typename Integer >
Integer	to_int (const cln::cl_RA &n)
template<>
sint	to_int< sint > (const cln::cl_I &n)
template<>
uint	to_int< uint > (const cln::cl_I &n)
template<typename To , typename From >
To	from_int (const From &n)
template<>
cln::cl_I	from_int (const uint &n)
template<>
cln::cl_I	from_int (const sint &n)
template<>
cln::cl_I	to_int< cln::cl_I > (const cln::cl_RA &n)
	Convert a fraction to an integer. More...
template<>
sint	to_int< sint > (const cln::cl_RA &n)
template<>
uint	to_int< uint > (const cln::cl_RA &n)
cln::cl_LF	to_lf (const cln::cl_RA &n)
	Convert a cln fraction to a cln long float. More...
template<>
cln::cl_RA	rationalize< cln::cl_RA > (double n)
template<>
cln::cl_RA	rationalize< cln::cl_RA > (float n)
template<>
cln::cl_RA	rationalize< cln::cl_RA > (int n)
template<>
cln::cl_RA	rationalize< cln::cl_RA > (uint n)
template<>
cln::cl_RA	rationalize< cln::cl_RA > (sint n)
template<>
cln::cl_I	parse< cln::cl_I > (const std::string &n)
template<>
bool	try_parse< cln::cl_I > (const std::string &n, cln::cl_I &res)
template<>
cln::cl_RA	parse< cln::cl_RA > (const std::string &n)
template<>
bool	try_parse< cln::cl_RA > (const std::string &n, cln::cl_RA &res)
cln::cl_I	abs (const cln::cl_I &n)
	Get absolute value of an integer. More...
cln::cl_RA	abs (const cln::cl_RA &n)
	Get absolute value of a fraction. More...
cln::cl_I	round (const cln::cl_RA &n)
	Round a fraction to next integer. More...
cln::cl_I	round (const cln::cl_I &n)
	Round an integer to next integer, that is do nothing. More...
cln::cl_I	floor (const cln::cl_RA &n)
	Round down a fraction. More...
cln::cl_I	floor (const cln::cl_I &n)
	Round down an integer. More...
cln::cl_I	ceil (const cln::cl_RA &n)
	Round up a fraction. More...
cln::cl_I	ceil (const cln::cl_I &n)
	Round up an integer. More...
cln::cl_I	gcd (const cln::cl_I &a, const cln::cl_I &b)
	Calculate the greatest common divisor of two integers. More...
cln::cl_I &	gcd_assign (cln::cl_I &a, const cln::cl_I &b)
	Calculate the greatest common divisor of two integers. More...
void	divide (const cln::cl_I &dividend, const cln::cl_I &divisor, cln::cl_I &quotient, cln::cl_I &remainder)
cln::cl_RA &	gcd_assign (cln::cl_RA &a, const cln::cl_RA &b)
	Calculate the greatest common divisor of two fractions. More...
cln::cl_RA	gcd (const cln::cl_RA &a, const cln::cl_RA &b)
	Calculate the greatest common divisor of two fractions. More...
cln::cl_I	lcm (const cln::cl_I &a, const cln::cl_I &b)
	Calculate the least common multiple of two integers. More...
cln::cl_RA	lcm (const cln::cl_RA &a, const cln::cl_RA &b)
	Calculate the least common multiple of two fractions. More...
template<>
cln::cl_RA	pow (const cln::cl_RA &basis, std::size_t exp)
	Calculate the power of some fraction to some positive integer. More...
cln::cl_RA	log (const cln::cl_RA &n)
cln::cl_RA	log10 (const cln::cl_RA &n)
cln::cl_RA	sin (const cln::cl_RA &n)
cln::cl_RA	cos (const cln::cl_RA &n)
bool	sqrt_exact (const cln::cl_RA &a, cln::cl_RA &b)
	Calculate the square root of a fraction if possible. More...
cln::cl_RA	sqrt (const cln::cl_RA &a)
std::pair< cln::cl_RA, cln::cl_RA >	sqrt_safe (const cln::cl_RA &a)
	Calculate the square root of a fraction. More...
std::pair< cln::cl_RA, cln::cl_RA >	sqrt_fast (const cln::cl_RA &a)
	Compute square root in a fast but less precise way. More...
std::pair< cln::cl_RA, cln::cl_RA >	root_safe (const cln::cl_RA &a, uint n)
cln::cl_I	mod (const cln::cl_I &a, const cln::cl_I &b)
	Calculate the remainder of the integer division. More...
cln::cl_RA	div (const cln::cl_RA &a, const cln::cl_RA &b)
	Divide two fractions. More...
cln::cl_I	div (const cln::cl_I &a, const cln::cl_I &b)
	Divide two integers. More...
cln::cl_RA &	div_assign (cln::cl_RA &a, const cln::cl_RA &b)
	Divide two fractions. More...
cln::cl_I &	div_assign (cln::cl_I &a, const cln::cl_I &b)
	Divide two integers. More...
cln::cl_RA	quotient (const cln::cl_RA &a, const cln::cl_RA &b)
	Divide two fractions. More...
cln::cl_I	quotient (const cln::cl_I &a, const cln::cl_I &b)
	Divide two integers. More...
cln::cl_I	remainder (const cln::cl_I &a, const cln::cl_I &b)
	Calculate the remainder of the integer division. More...
cln::cl_I	operator/ (const cln::cl_I &a, const cln::cl_I &b)
	Divide two integers. More...
cln::cl_I	operator/ (const cln::cl_I &lhs, const int &rhs)
cln::cl_RA	reciprocal (const cln::cl_RA &a)
std::string	toString (const cln::cl_RA &_number, bool _infix=true)
std::string	toString (const cln::cl_I &_number, bool _infix=true)
Str2Double_Error	str2double (double &d, char const *s)
template<typename Number >
bool	AlmostEqual2sComplement (const Number &A, const Number &B, unsigned=128)
template<>
bool	AlmostEqual2sComplement< double > (const double &A, const double &B, unsigned maxUlps)
template<typename FloatType >
bool	is_integer (const FLOAT_T< FloatType > &in)
template<typename FloatType >
FLOAT_T< FloatType >	div (const FLOAT_T< FloatType > &_lhs, const FLOAT_T< FloatType > &_rhs)
	Implements the division which assumes that there is no remainder. More...
template<typename FloatType >
FLOAT_T< FloatType >	quotient (const FLOAT_T< FloatType > &_lhs, const FLOAT_T< FloatType > &_rhs)
	Implements the division with remainder. More...
template<typename Integer , typename FloatType >
Integer	to_int (const FLOAT_T< FloatType > &_float)
	Casts the FLOAT_T to an arbitrary integer type which has a constructor for a native int. More...
template<typename FloatType >
double	to_double (const FLOAT_T< FloatType > &_float)
template<typename FloatType >
FLOAT_T< FloatType >	abs (const FLOAT_T< FloatType > &_in)
	Method which returns the absolute value of the passed number. More...
template<typename FloatType >
FLOAT_T< FloatType >	log (const FLOAT_T< FloatType > &_in)
	Method which returns the logarithm of the passed number. More...
template<typename FloatType >
FLOAT_T< FloatType >	sqrt (const FLOAT_T< FloatType > &_in)
	Method which returns the square root of the passed number. More...
template<typename FloatType >
std::pair< FLOAT_T< FloatType >, FLOAT_T< FloatType > >	sqrt_safe (const FLOAT_T< FloatType > &_in)
template<typename FloatType >
FLOAT_T< FloatType >	pow (const FLOAT_T< FloatType > &_in, size_t _exp)
template<typename FloatType >
FLOAT_T< FloatType >	sin (const FLOAT_T< FloatType > &_in)
template<typename FloatType >
FLOAT_T< FloatType >	cos (const FLOAT_T< FloatType > &_in)
template<typename FloatType >
FLOAT_T< FloatType >	asin (const FLOAT_T< FloatType > &_in)
template<typename FloatType >
FLOAT_T< FloatType >	acos (const FLOAT_T< FloatType > &_in)
template<typename FloatType >
FLOAT_T< FloatType >	atan (const FLOAT_T< FloatType > &_in)
template<typename FloatType >
FLOAT_T< FloatType >	floor (const FLOAT_T< FloatType > &_in)
	Method which returns the next smaller integer of this number or the number itself, if it is already an integer. More...
template<typename FloatType >
FLOAT_T< FloatType >	ceil (const FLOAT_T< FloatType > &_in)
	Method which returns the next larger integer of the passed number or the number itself, if it is already an integer. More...
template<>
FLOAT_T< double >	rationalize< FLOAT_T< double > > (double n)
template<>
FLOAT_T< float >	rationalize< FLOAT_T< float > > (float n)
template<>
FLOAT_T< mpq_class >	rationalize< FLOAT_T< mpq_class > > (double n)
mpz_class	get_denom (const FLOAT_T< mpq_class > &_in)
	Implicitly converts the number to a rational and returns the denominator. More...
mpz_class	get_num (const FLOAT_T< mpq_class > &_in)
	Implicitly converts the number to a rational and returns the nominator. More...
template<typename FloatType >
bool	is_zero (const FLOAT_T< FloatType > &_in)
template<typename FloatType >
bool	isInfinity (const FLOAT_T< FloatType > &_in)
template<typename FloatType >
bool	isNan (const FLOAT_T< FloatType > &_in)
template<>
bool	AlmostEqual2sComplement< FLOAT_T< double > > (const FLOAT_T< double > &A, const FLOAT_T< double > &B, unsigned maxUlps)
bool	sqrt_exact (const mpq_class &a, mpq_class &b)
	Calculate the square root of a fraction if possible. More...
mpq_class	sqrt (const mpq_class &a)
std::pair< mpq_class, mpq_class >	sqrt_safe (const mpq_class &a)
std::pair< mpq_class, mpq_class >	root_safe (const mpq_class &a, uint n)
	Calculate the nth root of a fraction. More...
std::pair< mpq_class, mpq_class >	sqrt_fast (const mpq_class &a)
	Compute square root in a fast but less precise way. More...
template<>
mpz_class	parse< mpz_class > (const std::string &n)
template<>
bool	try_parse< mpz_class > (const std::string &n, mpz_class &res)
template<>
mpq_class	parse< mpq_class > (const std::string &n)
template<>
bool	try_parse< mpq_class > (const std::string &n, mpq_class &res)
std::string	toString (const mpq_class &_number, bool _infix)
std::string	toString (const mpz_class &_number, bool _infix)
bool	is_zero (const mpz_class &n)
	Informational functions. More...
bool	is_zero (const mpq_class &n)
bool	is_one (const mpz_class &n)
bool	is_one (const mpq_class &n)
bool	is_positive (const mpz_class &n)
bool	is_positive (const mpq_class &n)
bool	is_negative (const mpz_class &n)
bool	is_negative (const mpq_class &n)
mpz_class	get_num (const mpq_class &n)
mpz_class	get_num (const mpz_class &n)
mpz_class	get_denom (const mpq_class &n)
mpz_class	get_denom (const mpz_class &n)
bool	is_integer (const mpq_class &n)
bool	is_integer (const mpz_class &)
std::size_t	bitsize (const mpz_class &n)
	Get the bit size of the representation of a integer. More...
std::size_t	bitsize (const mpq_class &n)
	Get the bit size of the representation of a fraction. More...
double	to_double (const mpq_class &n)
	Conversion functions. More...
double	to_double (const mpz_class &n)
template<typename Integer >
Integer	to_int (const mpz_class &n)
template<>
sint	to_int< sint > (const mpz_class &n)
template<>
uint	to_int< uint > (const mpz_class &n)
template<typename Integer >
Integer	to_int (const mpq_class &n)
template<>
mpz_class	to_int< mpz_class > (const mpq_class &n)
	Convert a fraction to an integer. More...
template<>
sint	to_int< sint > (const mpq_class &n)
	Convert a fraction to an unsigned. More...
template<>
uint	to_int< uint > (const mpq_class &n)
template<typename T >
T	rationalize (const PreventConversion< mpq_class > &)
template<>
mpq_class	rationalize< mpq_class > (float n)
template<>
mpq_class	rationalize< mpq_class > (double n)
template<>
mpq_class	rationalize< mpq_class > (int n)
template<>
mpq_class	rationalize< mpq_class > (uint n)
template<>
mpq_class	rationalize< mpq_class > (sint n)
template<>
mpq_class	rationalize< mpq_class > (const PreventConversion< mpq_class > &n)
mpz_class	abs (const mpz_class &n)
	Basic Operators. More...
mpq_class	abs (const mpq_class &n)
mpz_class	round (const mpq_class &n)
mpz_class	round (const mpz_class &n)
mpz_class	floor (const mpq_class &n)
mpz_class	floor (const mpz_class &n)
mpz_class	ceil (const mpq_class &n)
mpz_class	ceil (const mpz_class &n)
mpz_class	gcd (const mpz_class &a, const mpz_class &b)
mpz_class	lcm (const mpz_class &a, const mpz_class &b)
mpq_class	gcd (const mpq_class &a, const mpq_class &b)
mpz_class &	gcd_assign (mpz_class &a, const mpz_class &b)
	Calculate the greatest common divisor of two integers. More...
mpq_class &	gcd_assign (mpq_class &a, const mpq_class &b)
	Calculate the greatest common divisor of two integers. More...
mpq_class	lcm (const mpq_class &a, const mpq_class &b)
mpq_class	log (const mpq_class &n)
mpq_class	log10 (const mpq_class &n)
mpq_class	sin (const mpq_class &n)
mpq_class	cos (const mpq_class &n)
template<>
mpz_class	pow (const mpz_class &basis, std::size_t exp)
template<>
mpq_class	pow (const mpq_class &basis, std::size_t exp)
mpz_class	mod (const mpz_class &n, const mpz_class &m)
mpz_class	remainder (const mpz_class &n, const mpz_class &m)
mpz_class	quotient (const mpz_class &n, const mpz_class &d)
mpz_class	operator/ (const mpz_class &n, const mpz_class &d)
mpq_class	quotient (const mpq_class &n, const mpq_class &d)
mpq_class	operator/ (const mpq_class &n, const mpq_class &d)
void	divide (const mpz_class &dividend, const mpz_class &divisor, mpz_class &quotient, mpz_class &remainder)
mpq_class	div (const mpq_class &a, const mpq_class &b)
	Divide two fractions. More...
mpz_class	div (const mpz_class &a, const mpz_class &b)
	Divide two integers. More...
mpz_class &	div_assign (mpz_class &a, const mpz_class &b)
	Divide two integers. More...
mpq_class &	div_assign (mpq_class &a, const mpq_class &b)
	Divide two integers. More...
mpq_class	reciprocal (const mpq_class &a)
mpq_class	operator* (const mpq_class &lhs, const mpq_class &rhs)
bool	is_zero (double n)
	Informational functions. More...
bool	is_positive (double n)
bool	is_negative (double n)
bool	isNaN (double d)
bool	isInf (double d)
bool	is_number (double d)
bool	is_integer (double d)
bool	is_integer (sint)
std::size_t	bitsize (unsigned)
double	to_double (sint n)
	Conversion functions. More...
double	to_double (double n)
template<typename Integer >
Integer	to_int (double n)
template<>
sint	to_int< sint > (double n)
template<>
uint	to_int< uint > (double n)
template<>
double	rationalize (double n)
template<typename T >
std::enable_if< std::is_arithmetic< typename remove_all< T >::type >::value, std::string >::type	toString (const T &n, bool)
double	floor (double n)
	Basic Operators. More...
double	ceil (double n)
double	abs (double n)
uint	mod (uint n, uint m)
sint	mod (sint n, sint m)
sint	remainder (sint n, sint m)
sint	div (sint n, sint m)
sint	quotient (sint n, sint m)
void	divide (sint dividend, sint divisor, sint &quo, sint &rem)
double	sin (double in)
double	cos (double in)
double	acos (double in)
double	sqrt (double in)
std::pair< double, double >	sqrt_safe (double in)
double	pow (double in, uint exp)
double	log (double in)
double	log10 (double in)
template<typename Number >
Number	highestPower (const Number &n)
	Returns the highest power of two below n. More...
template<typename From , typename To , carl::DisableIf< std::is_same< From, To > > >
To	convert (const From &)
template<typename Rational >
double	roundDown (const Rational &o, bool overapproximate=false)
	Returns a down-rounded representation of the given numeric. More...
template<typename Rational >
double	roundUp (const Rational &o, bool overapproximate=false)
	Returns a up-rounded representation of the given numeric. More...
template<>
mpq_class	convert< double, mpq_class > (const double &n)
template<>
double	convert< mpq_class, double > (const mpq_class &n)
template<>
FLOAT_T< mpq_class >	convert< double, FLOAT_T< mpq_class > > (const double &n)
template<>
double	convert< FLOAT_T< mpq_class >, double > (const FLOAT_T< mpq_class > &n)
template<>
FLOAT_T< double >	convert< mpq_class, FLOAT_T< double > > (const mpq_class &n)
template<>
mpq_class	convert< FLOAT_T< double >, mpq_class > (const FLOAT_T< double > &n)
template<>
mpq_class	convert< FLOAT_T< mpq_class >, mpq_class > (const FLOAT_T< mpq_class > &n)
template<>
FLOAT_T< mpq_class >	convert< mpq_class, FLOAT_T< mpq_class > > (const mpq_class &n)
template<>
double	convert< FLOAT_T< double >, double > (const FLOAT_T< double > &n)
template<>
FLOAT_T< double >	convert< double, FLOAT_T< double > > (const double &n)
template<typename IntegerT >
bool	is_zero (const GFNumber< IntegerT > &_in)
template<typename IntegerT >
bool	is_one (const GFNumber< IntegerT > &_in)
template<typename IntegerT >
GFNumber< IntegerT >	quotient (const GFNumber< IntegerT > &lhs, const GFNumber< IntegerT > &rhs)
template<typename IntegerT >
GFNumber< IntegerT >	abs (const GFNumber< IntegerT > &n)
template<typename IntegerT >
bool	is_integer (const GFNumber< IntegerT > &)
template<typename IntegerType >
std::string	toString (const GFNumber< IntegerType > &_number, bool)
	Creates the string representation to the given galois field number. More...
template<typename T >
bool	is_zero (const T &t)
template<typename T >
bool	is_one (const T &t)
template<typename T , EnableIf< has_is_positive< T >> >
bool	is_positive (const T &t)
template<typename T , EnableIf< has_is_negative< T >> >
bool	is_negative (const T &t)
template<typename T , DisableIf< is_interval_type< T >> = dummy>
T	pow (const T &basis, std::size_t exp)
	Implements a fast exponentiation on an arbitrary type T. More...
template<typename T >
void	pow_assign (T &t, std::size_t exp)
	Implements a fast exponentiation on an arbitrary type T. More...
template<typename T >
T	rationalize (float n)
template<typename T >
T	rationalize (int n)
template<typename T >
T	rationalize (sint n)
template<typename T >
T	rationalize (uint n)
template<typename Number >
int	to_int (const Number &n)
template<typename T >
T	parse (const std::string &n)
template<typename T >
bool	try_parse (const std::string &n, T &res)
template<typename T , typename T2 >
bool	fits_within (const T2 &t)
template<typename T , typename S , std::enable_if_t< is_polynomial_type< T >::value &&is_polynomial_type< S >::value &&!needs_context_type< T >::value, int > = 0>
T	convert (const S &r)
template<typename T , typename S , std::enable_if_t< is_polynomial_type< T >::value &&is_polynomial_type< S >::value &&needs_context_type< T >::value, int > = 0>
T	convert (const typename T::ContextType &c, const S &r)
std::ostream &	operator<< (std::ostream &os, const Context &ctx)
template<typename Coeff , typename Ordering , typename Policies >
bool	is_constant (const ContextPolynomial< Coeff, Ordering, Policies > &p)
template<typename Coeff , typename Ordering , typename Policies >
bool	is_zero (const ContextPolynomial< Coeff, Ordering, Policies > &p)
template<typename Coeff , typename Ordering , typename Policies >
bool	is_linear (const ContextPolynomial< Coeff, Ordering, Policies > &p)
template<typename Coeff , typename Ordering , typename Policies >
bool	is_number (const ContextPolynomial< Coeff, Ordering, Policies > &p)
template<typename Coeff , typename Ordering , typename Policies >
std::size_t	level_of (const ContextPolynomial< Coeff, Ordering, Policies > &p)
template<typename Coeff , typename Ordering , typename Policies >
void	variables (const ContextPolynomial< Coeff, Ordering, Policies > &p, carlVariables &vars)
template<typename Coeff , typename Ordering , typename Policies >
bool	operator< (const ContextPolynomial< Coeff, Ordering, Policies > &lhs, const ContextPolynomial< Coeff, Ordering, Policies > &rhs)
template<typename Coeff , typename Ordering , typename Policies >
bool	operator== (const ContextPolynomial< Coeff, Ordering, Policies > &lhs, const ContextPolynomial< Coeff, Ordering, Policies > &rhs)
template<typename Coeff , typename Ordering , typename Policies >
std::ostream &	operator<< (std::ostream &os, const ContextPolynomial< Coeff, Ordering, Policies > &rhs)
template<typename Coeff , typename Ordering , typename Policies >
auto	irreducible_factors (const ContextPolynomial< Coeff, Ordering, Policies > &p, bool constants=true)
template<typename Coeff , typename Ordering , typename Policies >
auto	discriminant (const ContextPolynomial< Coeff, Ordering, Policies > &p)
template<typename Coeff , typename Ordering , typename Policies >
auto	resultant (const ContextPolynomial< Coeff, Ordering, Policies > &p, const ContextPolynomial< Coeff, Ordering, Policies > &q)
std::size_t	bitsize (const Monomial &m)
template<typename Coeff >
std::size_t	bitsize (const Term< Coeff > &t)
template<typename Coeff , typename Ordering , typename Policies >
std::size_t	bitsize (const MultivariatePolynomial< Coeff, Ordering, Policies > &p)
std::size_t	complexity (const Monomial &m)
template<typename Coeff >
std::size_t	complexity (const Term< Coeff > &t)
template<typename Coeff , typename Ordering , typename Policies >
std::size_t	complexity (const MultivariatePolynomial< Coeff, Ordering, Policies > &p)
template<typename Coeff >
std::size_t	complexity (const UnivariatePolynomial< Coeff > &p)
template<typename Coeff >
Coeff	content (const UnivariatePolynomial< Coeff > &p)
	The content of a polynomial is the gcd of the coefficients of the normal part of a polynomial. More...
template<typename C , typename O , typename P >
MultivariatePolynomial< C, O, P >	coprimePart (const MultivariatePolynomial< C, O, P > &p, const MultivariatePolynomial< C, O, P > &q)
	Calculates the coprime part of p and q. More...
std::ostream &	operator<< (std::ostream &os, Definiteness d)
template<typename Coeff >
Definiteness	definiteness (const Term< Coeff > &t)
template<typename C , typename O , typename P >
Definiteness	definiteness (const MultivariatePolynomial< C, O, P > &p, bool full_effort=true)
auto	total_degree (const Monomial &m)
	Gives the total degree, i.e. More...
bool	is_constant (const Monomial &m)
	Checks whether the monomial is a constant. More...
bool	is_linear (const Monomial &m)
	Checks whether the monomial has exactly degree one. More...
bool	is_at_most_linear (const Monomial &m)
	Checks whether the monomial has at most degree one. More...
template<typename Coeff >
std::size_t	total_degree (const Term< Coeff > &t)
	Gives the total degree, i.e. More...
template<typename Coeff >
bool	is_constant (const Term< Coeff > &t)
	Checks whether the monomial is a constant. More...
template<typename Coeff >
bool	is_linear (const Term< Coeff > &t)
	Checks whether the monomial has exactly the degree one. More...
template<typename Coeff >
bool	is_at_most_linear (const Term< Coeff > &t)
	Checks whether the monomial has at most degree one. More...
template<typename Coeff , typename Ordering , typename Policies >
std::size_t	total_degree (const MultivariatePolynomial< Coeff, Ordering, Policies > &p)
	Calculates the max. More...
template<typename Coeff , typename Ordering , typename Policies >
bool	is_constant (const MultivariatePolynomial< Coeff, Ordering, Policies > &p)
	Check if the polynomial is linear. More...
template<typename Coeff , typename Ordering , typename Policies >
bool	is_linear (const MultivariatePolynomial< Coeff, Ordering, Policies > &p)
	Check if the polynomial is linear. More...
template<typename Coeff >
std::size_t	total_degree (const UnivariatePolynomial< Coeff > &p)
	Returns the total degree of the polynomial, that is the maximum degree of any monomial. More...
template<typename Coeff >
bool	is_constant (const UnivariatePolynomial< Coeff > &p)
	Checks whether the polynomial is constant with respect to the main variable. More...
template<typename Coeff >
bool	is_linear (const UnivariatePolynomial< Coeff > &p)
template<typename T , EnableIf< is_number_type< T >> = dummy>
const T &	derivative (const T &t, Variable, std::size_t n=1)
	Computes the n'th derivative of a number, which is either the number itself (for n = 0) or zero. More...
std::pair< std::size_t, Monomial::Arg >	derivative (const Monomial::Arg &m, Variable v, std::size_t n=1)
	Computes the (partial) n'th derivative of this monomial with respect to the given variable. More...
template<typename C >
Term< C >	derivative (const Term< C > &t, Variable v, std::size_t n=1)
	Computes the n'th derivative of t with respect to v. More...
template<typename C , typename O , typename P >
MultivariatePolynomial< C, O, P >	derivative (const MultivariatePolynomial< C, O, P > &p, Variable v, std::size_t n=1)
	Computes the n'th derivative of p with respect to v. More...
template<typename C >
UnivariatePolynomial< C >	derivative (const UnivariatePolynomial< C > &p, std::size_t n=1)
	Computes the n'th derivative of p with respect to the main variable of p. More...
template<typename C >
UnivariatePolynomial< C >	derivative (const UnivariatePolynomial< C > &p, Variable v, std::size_t n=1)
	Computes the n'th derivative of p with respect to v. More...
template<typename T >
std::vector< T >	solveDiophantine (MultivariatePolynomial< T > &p)
	Diophantine Equations solver. More...
template<typename T >
T	extended_gcd_integer (T a, T b, T &s, T &t)
template<typename Coeff >
Term< Coeff >	divide (const Term< Coeff > &t, const Coeff &c)
template<typename Coeff >
bool	try_divide (const Term< Coeff > &t, const Coeff &c, Term< Coeff > &res)
template<typename Coeff >
bool	try_divide (const Term< Coeff > &t, Variable v, Term< Coeff > &res)
template<typename Coeff , typename Ordering , typename Policies >
MultivariatePolynomial< Coeff, Ordering, Policies >	divide (const MultivariatePolynomial< Coeff, Ordering, Policies > &p, const Coeff &divisor)
	Divides the polynomial by the given coefficient. More...
template<typename Coeff , typename Ordering , typename Policies >
bool	try_divide (const MultivariatePolynomial< Coeff, Ordering, Policies > &dividend, const MultivariatePolynomial< Coeff, Ordering, Policies > &divisor, MultivariatePolynomial< Coeff, Ordering, Policies > &quotient)
	Divides the polynomial by another polynomial. More...
template<typename Coeff , typename Ordering , typename Policies >
DivisionResult< MultivariatePolynomial< Coeff, Ordering, Policies > >	divide (const MultivariatePolynomial< Coeff, Ordering, Policies > &dividend, const MultivariatePolynomial< Coeff, Ordering, Policies > &divisor)
	Calculating the quotient and the remainder, such that for a given polynomial p we have p = divisor * quotient + remainder. More...
template<typename Coeff >
bool	try_divide (const UnivariatePolynomial< Coeff > &dividend, const Coeff &divisor, UnivariatePolynomial< Coeff > &quotient)
template<typename Coeff >
DivisionResult< UnivariatePolynomial< Coeff > >	divide (const UnivariatePolynomial< Coeff > &p, const Coeff &divisor)
template<typename Coeff >
DivisionResult< UnivariatePolynomial< Coeff > >	divide (const UnivariatePolynomial< Coeff > &p, const typename UnderlyingNumberType< Coeff >::type &divisor)
template<typename Coeff >
DivisionResult< UnivariatePolynomial< Coeff > >	divide (const UnivariatePolynomial< Coeff > &dividend, const UnivariatePolynomial< Coeff > &divisor)
	Divides the polynomial by another polynomial. More...
template<typename C , typename O , typename P >
MultivariatePolynomial< C, O, P >	operator/ (const MultivariatePolynomial< C, O, P > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
template<typename Coefficient >
Coefficient	evaluate (const Monomial &m, const std::map< Variable, Coefficient > &substitutions)
template<typename Coefficient >
Coefficient	evaluate (const Term< Coefficient > &t, const std::map< Variable, Coefficient > &map)
template<typename C , typename O , typename P , typename SubstitutionType >
SubstitutionType	evaluate (const MultivariatePolynomial< C, O, P > &p, const std::map< Variable, SubstitutionType > &substitutions)
	Like substitute, but expects substitutions for all variables. More...
template<typename Coeff >
Coeff	evaluate (const UnivariatePolynomial< Coeff > &p, const Coeff &value)
template<typename Coeff >
bool	is_root_of (const UnivariatePolynomial< Coeff > &p, const Coeff &value)
template<typename C , typename O , typename P >
Factors< MultivariatePolynomial< C, O, P > >	factorization (const MultivariatePolynomial< C, O, P > &p, bool includeConstants=true)
	Try to factorize a multivariate polynomial. More...
template<typename C , typename O , typename P >
bool	is_trivial (const Factors< MultivariatePolynomial< C, O, P >> &f)
template<typename C , typename O , typename P >
std::vector< MultivariatePolynomial< C, O, P > >	irreducible_factors (const MultivariatePolynomial< C, O, P > &p, bool includeConstants=true)
	Try to factorize a multivariate polynomial and return the irreducible factors (without multiplicities). More...
template<typename Coeff >
std::map< uint, UnivariatePolynomial< Coeff > >	squareFreeFactorization (const UnivariatePolynomial< Coeff > &p)
template<typename Coeff >
FactorMap< Coeff >	factorization (const UnivariatePolynomial< Coeff > &p)
template<typename C , typename O , typename P >
MultivariatePolynomial< C, O, P >	gcd (const MultivariatePolynomial< C, O, P > &a, const MultivariatePolynomial< C, O, P > &b)
template<typename Coeff >
UnivariatePolynomial< Coeff >	gcd (const UnivariatePolynomial< Coeff > &a, const UnivariatePolynomial< Coeff > &b)
	Calculates the greatest common divisor of two polynomials. More...
template<typename C , typename O , typename P >
Term< C >	gcd (const MultivariatePolynomial< C, O, P > &a, const Term< C > &b)
template<typename C , typename O , typename P >
Term< C >	gcd (const Term< C > &a, const MultivariatePolynomial< C, O, P > &b)
template<typename C , typename O , typename P >
Monomial::Arg	gcd (const MultivariatePolynomial< C, O, P > &a, const Monomial::Arg &b)
template<typename C , typename O , typename P >
Monomial::Arg	gcd (const Monomial::Arg &a, const MultivariatePolynomial< C, O, P > &b)
Monomial::Arg	gcd (const Monomial::Arg &lhs, const Monomial::Arg &rhs)
	Calculates the least common multiple of two monomial pointers. More...
template<typename Coeff >
Term< Coeff >	gcd (const Term< Coeff > &t1, const Term< Coeff > &t2)
	Calculates the gcd of (t1, t2). More...
template<typename Coeff >
UnivariatePolynomial< Coeff >	gcd_recursive (const UnivariatePolynomial< Coeff > &a, const UnivariatePolynomial< Coeff > &b)
template<typename Coeff >
UnivariatePolynomial< Coeff >	extended_gcd (const UnivariatePolynomial< Coeff > &a, const UnivariatePolynomial< Coeff > &b, UnivariatePolynomial< Coeff > &s, UnivariatePolynomial< Coeff > &t)
	Calculates the extended greatest common divisor g of two polynomials. More...
template<typename C , typename O , typename P >
std::vector< MultivariatePolynomial< C, O, P > >	groebner_basis (const std::vector< MultivariatePolynomial< C, O, P >> &polys)
template<typename PolynomialType , typename Number , class strategy >
Interval< Number >	evaluate (const MultivariateHorner< PolynomialType, strategy > &mvH, const std::map< Variable, Interval< Number >> &map)
template<typename Numeric >
Interval< Numeric >	evaluate (const Monomial &m, const std::map< Variable, Interval< Numeric >> &map)
template<typename Coeff , typename Numeric , EnableIf< std::is_same< Numeric, Coeff >> = dummy>
Interval< Numeric >	evaluate (const Term< Coeff > &t, const std::map< Variable, Interval< Numeric >> &map)
template<typename Coeff , typename Policy , typename Ordering , typename Numeric >
Interval< Numeric >	evaluate (const MultivariatePolynomial< Coeff, Policy, Ordering > &p, const std::map< Variable, Interval< Numeric >> &map)
template<typename Numeric , typename Coeff , EnableIf< std::is_same< Numeric, Coeff >> = dummy>
Interval< Numeric >	evaluate (const UnivariatePolynomial< Coeff > &p, const std::map< Variable, Interval< Numeric >> &map)
template<typename C , typename O , typename P >
MultivariatePolynomial< C, O, P >	lcm (const MultivariatePolynomial< C, O, P > &a, const MultivariatePolynomial< C, O, P > &b)
Monomial::Arg	pow (const Monomial &m, uint exp)
	Calculates the given power of a monomial m. More...
Monomial::Arg	pow (const Monomial::Arg &m, uint exp)
template<typename Coeff >
Term< Coeff >	pow (const Term< Coeff > &t, uint exp)
template<typename C , typename O , typename P >
MultivariatePolynomial< C, O, P >	pow (const MultivariatePolynomial< C, O, P > &p, std::size_t exp)
template<typename C , typename O , typename P >
MultivariatePolynomial< C, O, P >	pow_naive (const MultivariatePolynomial< C, O, P > &p, std::size_t exp)
template<typename Coeff >
UnivariatePolynomial< Coeff >	pow (const UnivariatePolynomial< Coeff > &p, std::size_t exp)
	Returns a polynomial to the given power. More...
template<typename Coeff >
UnivariatePolynomial< Coeff >	primitive_euclidean (const UnivariatePolynomial< Coeff > &a, const UnivariatePolynomial< Coeff > &b)
	Computes the GCD of two univariate polynomial with coefficients from a unique factorization domain using the primitive euclidean algorithm. More...
template<typename Coeff >
UnivariatePolynomial< Coeff >	primitive_part (const UnivariatePolynomial< Coeff > &p)
	The primitive part of p is the normal part of p divided by the content of p. More...
template<typename Coeff >
UnivariatePolynomial< Coeff >	pseudo_primitive_part (const UnivariatePolynomial< Coeff > &p)
	Returns this/divisor where divisor is the numeric content of this polynomial. More...
template<typename C , typename O , typename P >
MultivariatePolynomial< C, O, P >	quotient (const MultivariatePolynomial< C, O, P > &dividend, const MultivariatePolynomial< C, O, P > &divisor)
	Calculates the quotient of a polynomial division. More...
template<typename Coeff >
UnivariatePolynomial< Coeff >	remainder_helper (const UnivariatePolynomial< Coeff > &dividend, const UnivariatePolynomial< Coeff > &divisor, const Coeff *prefactor=nullptr)
	Does the heavy lifting for the remainder computation of polynomial division. More...
template<typename Coeff >
UnivariatePolynomial< Coeff >	remainder (const UnivariatePolynomial< Coeff > &dividend, const UnivariatePolynomial< Coeff > &divisor, const Coeff &prefactor)
template<typename Coeff >
UnivariatePolynomial< Coeff >	remainder (const UnivariatePolynomial< Coeff > &dividend, const UnivariatePolynomial< Coeff > &divisor)
template<typename Coeff >
UnivariatePolynomial< Coeff >	pseudo_remainder (const UnivariatePolynomial< Coeff > &dividend, const UnivariatePolynomial< Coeff > &divisor)
	Calculates the pseudo-remainder. More...
template<typename Coeff >
UnivariatePolynomial< Coeff >	signed_pseudo_remainder (const UnivariatePolynomial< Coeff > &dividend, const UnivariatePolynomial< Coeff > &divisor)
	Compute the signed pseudo-remainder. More...
template<typename C , typename O , typename P >
MultivariatePolynomial< C, O, P >	remainder (const MultivariatePolynomial< C, O, P > &dividend, const MultivariatePolynomial< C, O, P > &divisor)
template<typename C , typename O , typename P >
MultivariatePolynomial< C, O, P >	pseudo_remainder (const MultivariatePolynomial< C, O, P > &dividend, const MultivariatePolynomial< C, O, P > &divisor, Variable var)
template<typename Coeff >
UnivariatePolynomial< MultivariatePolynomial< typename UnderlyingNumberType< Coeff >::type > >	switch_main_variable (const UnivariatePolynomial< Coeff > &p, Variable newVar)
	Switches the main variable using a purely syntactical restructuring. More...
template<typename Coeff >
UnivariatePolynomial< Coeff >	replace_main_variable (const UnivariatePolynomial< Coeff > &p, Variable newVar)
	Replaces the main variable in a polynomial. More...
template<typename C , typename O , typename P >
MultivariatePolynomial< C, O, P >	switch_variable (const MultivariatePolynomial< C, O, P > &p, Variable old_var, Variable new_var)
template<typename Coeff >
std::list< UnivariatePolynomial< Coeff > >	subresultants (const UnivariatePolynomial< Coeff > &pol1, const UnivariatePolynomial< Coeff > &pol2, SubresultantStrategy strategy)
	Implements a subresultants algorithm with optimizations described in [2] . More...
template<typename Coeff >
std::vector< UnivariatePolynomial< Coeff > >	principalSubresultantsCoefficients (const UnivariatePolynomial< Coeff > &, const UnivariatePolynomial< Coeff > &, SubresultantStrategy=SubresultantStrategy::Default)
template<typename Coeff >
UnivariatePolynomial< Coeff >	resultant (const UnivariatePolynomial< Coeff > &, const UnivariatePolynomial< Coeff > &, SubresultantStrategy=SubresultantStrategy::Default)
template<typename Coeff >
UnivariatePolynomial< Coeff >	discriminant (const UnivariatePolynomial< Coeff > &, SubresultantStrategy=SubresultantStrategy::Default)
template<typename Coeff >
Coeff	cauchyBound (const UnivariatePolynomial< Coeff > &p)
template<typename Coeff >
Coeff	hirstMaceyBound (const UnivariatePolynomial< Coeff > &p)
template<typename Coeff >
Coeff	lagrangeBound (const UnivariatePolynomial< Coeff > &p)
template<typename Coeff >
Coeff	lagrangePositiveUpperBound (const UnivariatePolynomial< Coeff > &p)
template<typename Coeff >
Coeff	lagrangePositiveLowerBound (const UnivariatePolynomial< Coeff > &p)
	Computes a lower bound on the value of the positive real roots of the given univariate polynomial. More...
template<typename Coeff >
Coeff	lagrangeNegativeUpperBound (const UnivariatePolynomial< Coeff > &p)
	Computes an upper bound on the value of the negative real roots of the given univariate polynomial. More...
template<typename Coefficient >
int	count_real_roots (const std::vector< UnivariatePolynomial< Coefficient >> &seq, const Interval< Coefficient > &i)
	Calculate the number of real roots of a polynomial within a given interval based on a sturm sequence of this polynomial. More...
template<typename Coefficient >
int	count_real_roots (const UnivariatePolynomial< Coefficient > &p, const Interval< Coefficient > &i)
	Count the number of real roots of p within the given interval using Sturm sequences. More...
template<typename Coeff >
void	eliminate_zero_root (UnivariatePolynomial< Coeff > &p)
	Reduces the given polynomial such that zero is not a root anymore. More...
template<typename Coeff >
void	eliminate_root (UnivariatePolynomial< Coeff > &p, const Coeff &root)
	Reduces the polynomial such that the given root is not a root anymore. More...
Monomial::Arg	separable_part (const Monomial &m)
	Calculates the separable part of this monomial. More...
template<typename Coefficient >
uint	sign_variations (const UnivariatePolynomial< Coefficient > &polynomial, const Interval< Coefficient > &interval)
	Counts the sign variations (i.e. More...
template<typename C , typename O , typename P >
std::vector< std::pair< C, MultivariatePolynomial< C, O, P > > >	sos_decomposition (const MultivariatePolynomial< C, O, P > &p, bool not_trivial=false)
template<typename C , typename O , typename P >
MultivariatePolynomial< C, O, P >	SPolynomial (const MultivariatePolynomial< C, O, P > &p, const MultivariatePolynomial< C, O, P > &q)
	Calculates the S-Polynomial of two polynomials. More...
template<typename C , typename O , typename P >
MultivariatePolynomial< C, O, P >	squareFreePart (const MultivariatePolynomial< C, O, P > &polynomial)
template<typename Coeff , EnableIf< is_subset_of_rationals_type< Coeff >> = dummy>
UnivariatePolynomial< Coeff >	squareFreePart (const UnivariatePolynomial< Coeff > &p)
template<typename Coeff >
std::vector< UnivariatePolynomial< Coeff > >	sturm_sequence (const UnivariatePolynomial< Coeff > &p, const UnivariatePolynomial< Coeff > &q)
	Computes the sturm sequence of two polynomials. More...
template<typename Coeff >
std::vector< UnivariatePolynomial< Coeff > >	sturm_sequence (const UnivariatePolynomial< Coeff > &p)
	Computes the sturm sequence of a polynomial as defined at [3], page 333, example 22. More...
template<typename Coeff >
Coeff	substitute (const Monomial &m, const std::map< Variable, Coeff > &substitutions)
	Applies the given substitutions to a monomial. More...
template<typename Coeff >
Term< Coeff >	substitute (const Term< Coeff > &t, const std::map< Variable, Coeff > &substitutions)
template<typename Coeff >
Term< Coeff >	substitute (const Term< Coeff > &t, const std::map< Variable, Term< Coeff >> &substitutions)
template<typename C , typename O , typename P >
void	substitute_inplace (MultivariatePolynomial< C, O, P > &p, Variable var, const MultivariatePolynomial< C, O, P > &value)
template<typename C , typename O , typename P >
MultivariatePolynomial< C, O, P >	substitute (const MultivariatePolynomial< C, O, P > &p, Variable var, const MultivariatePolynomial< C, O, P > &value)
template<typename C , typename O , typename P , typename S >
MultivariatePolynomial< C, O, P >	substitute (const MultivariatePolynomial< C, O, P > &p, const std::map< Variable, S > &substitutions)
template<typename C , typename O , typename P >
MultivariatePolynomial< C, O, P >	substitute (const MultivariatePolynomial< C, O, P > &p, const std::map< Variable, Term< C >> &substitutions)
template<typename C , typename O , typename P >
MultivariatePolynomial< C, O, P >	substitute (const MultivariatePolynomial< C, O, P > &p, const std::map< Variable, MultivariatePolynomial< C, O, P >> &substitutions)
template<typename Coeff >
void	substitute_inplace (UnivariatePolynomial< Coeff > &p, Variable var, const Coeff &value)
template<typename Coeff >
UnivariatePolynomial< Coeff >	substitute (const UnivariatePolynomial< Coeff > &p, Variable var, const Coeff &value)
template<typename Rational >
void	substitute_inplace (MultivariatePolynomial< Rational > &p, Variable var, const Rational &r)
	Substitutes a variable with a rational within a polynomial. More...
template<typename Poly , typename Rational >
void	substitute_inplace (UnivariatePolynomial< Poly > &p, Variable var, const Rational &r)
template<typename C , typename O , typename P >
UnivariatePolynomial< C >	to_univariate_polynomial (const MultivariatePolynomial< C, O, P > &p)
	Convert a univariate polynomial that is currently (mis)represented by a 'MultivariatePolynomial' into a more appropiate 'UnivariatePolynomial' representation. More...
template<typename C , typename O , typename P >
UnivariatePolynomial< MultivariatePolynomial< C, O, P > >	to_univariate_polynomial (const MultivariatePolynomial< C, O, P > &p, Variable v)
	Convert a multivariate polynomial that is currently represented by a MultivariatePolynomial into a UnivariatePolynomial representation. More...
template<typename Coeff , typename Ordering , typename Policies >
VarInfo< MultivariatePolynomial< Coeff, Ordering, Policies > >	var_info (const MultivariatePolynomial< Coeff, Ordering, Policies > &poly, const Variable var, bool collect_coeff=false)
template<typename Coeff , typename Ordering , typename Policies >
VarsInfo< MultivariatePolynomial< Coeff, Ordering, Policies > >	vars_info (const MultivariatePolynomial< Coeff, Ordering, Policies > &poly, bool collect_coeff=false)
Monomial::Arg	pow (Variable v, std::size_t exp)
bool	operator== (const std::pair< Variable, std::size_t > &p, Variable v)
	Compare a pair of variable and exponent with a variable. More...
std::ostream &	operator<< (std::ostream &os, const Monomial &rhs)
	Streaming operator for Monomial. More...
std::ostream &	operator<< (std::ostream &os, const Monomial::Arg &rhs)
	Streaming operator for std::shared_ptr<Monomial>. More...
void	variables (const Monomial &m, carlVariables &vars)
	Add the variables of the given monomial to the variables. More...
std::size_t	hash_value (const carl::Monomial &monomial)
std::ostream &	operator<< (std::ostream &os, const MonomialPool &mp)
template<typename... T>
Monomial::Arg	createMonomial (T &&... t)
template<typename C , typename O , typename P >
bool	is_one (const MultivariatePolynomial< C, O, P > &p)
template<typename C , typename O , typename P >
bool	is_zero (const MultivariatePolynomial< C, O, P > &p)
template<typename C , typename O , typename P >
std::pair< MultivariatePolynomial< C, O, P >, MultivariatePolynomial< C, O, P > >	lazyDiv (const MultivariatePolynomial< C, O, P > &_polyA, const MultivariatePolynomial< C, O, P > &_polyB)
template<typename C , typename O , typename P >
std::ostream &	operator<< (std::ostream &os, const MultivariatePolynomial< C, O, P > &rhs)
	Streaming operator for multivariate polynomials. More...
template<typename Coeff , typename Ordering , typename Policies >
void	variables (const MultivariatePolynomial< Coeff, Ordering, Policies > &p, carlVariables &vars)
	Add the variables of the given polynomial to the variables. More...
template<typename Coeff >
bool	is_zero (const Term< Coeff > &term)
	Checks whether a term is zero. More...
template<typename Coeff >
void	variables (const Term< Coeff > &t, carlVariables &vars)
	Add the variables of the given term to the variables. More...
template<typename Coeff >
bool	is_one (const Term< Coeff > &term)
	Checks whether a term is one. More...
template<typename Coeff >
Term< Coeff >	operator- (const Term< Coeff > &rhs)
template<typename Coefficient >
bool	is_zero (const UnivariatePolynomial< Coefficient > &p)
	Checks if the polynomial is equal to zero. More...
template<typename Coefficient >
bool	is_one (const UnivariatePolynomial< Coefficient > &p)
	Checks if the polynomial is equal to one. More...
template<typename Coeff >
void	variables (const UnivariatePolynomial< Coeff > &p, carlVariables &vars)
	Add the variables of the given polynomial to the variables. More...
template<typename Number , typename = std::enable_if_t<is_number_type<Number>::value>>
const Number &	branching_point (const Number &n)
template<typename Number , typename = std::enable_if_t<is_number_type<Number>::value>>
Number	sample_above (const Number &n)
template<typename Number , typename = std::enable_if_t<is_number_type<Number>::value>>
Number	sample_below (const Number &n)
template<typename Number , typename = std::enable_if_t<is_number_type<Number>::value>>
Number	sample_between (const Number &lower, const Number &upper)
template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>
Number	is_root_of (const UnivariatePolynomial< Number > &p, const RAN &value)
template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>
bool	operator== (const RAN &lhs, const Number &rhs)
template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>
bool	operator!= (const RAN &lhs, const Number &rhs)
template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>
bool	operator<= (const RAN &lhs, const Number &rhs)
template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>
bool	operator>= (const RAN &lhs, const Number &rhs)
template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>
bool	operator< (const RAN &lhs, const Number &rhs)
template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>
bool	operator> (const RAN &lhs, const Number &rhs)
template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>
bool	operator== (const Number &lhs, const RAN &rhs)
template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>
bool	operator!= (const Number &lhs, const RAN &rhs)
template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>
bool	operator<= (const Number &lhs, const RAN &rhs)
template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>
bool	operator>= (const Number &lhs, const RAN &rhs)
template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>
bool	operator< (const Number &lhs, const RAN &rhs)
template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>
bool	operator> (const Number &lhs, const RAN &rhs)
template<typename RAN , EnableIf< is_ran_type< RAN >> = dummy>
bool	operator== (const RAN &lhs, const RAN &rhs)
template<typename RAN , EnableIf< is_ran_type< RAN >> = dummy>
bool	operator!= (const RAN &lhs, const RAN &rhs)
template<typename RAN , EnableIf< is_ran_type< RAN >> = dummy>
bool	operator<= (const RAN &lhs, const RAN &rhs)
template<typename RAN , EnableIf< is_ran_type< RAN >> = dummy>
bool	operator>= (const RAN &lhs, const RAN &rhs)
template<typename RAN , EnableIf< is_ran_type< RAN >> = dummy>
bool	operator< (const RAN &lhs, const RAN &rhs)
template<typename RAN , EnableIf< is_ran_type< RAN >> = dummy>
bool	operator> (const RAN &lhs, const RAN &rhs)
template<typename T , std::enable_if_t< is_ran_type< T >::value, int > = 0>
T	convert (const T &r)
template<typename Number >
std::optional< IntRepRealAlgebraicNumber< Number > >	evaluate (MultivariatePolynomial< Number > p, const Assignment< IntRepRealAlgebraicNumber< Number >> &m, bool refine_model=true)
	Evaluate the given polynomial with the given values for the variables. More...
template<typename Number >
boost::tribool	evaluate (const BasicConstraint< MultivariatePolynomial< Number >> &c, const Assignment< IntRepRealAlgebraicNumber< Number >> &m, bool refine_model=true, bool use_root_bounds=true)
template<typename Coeff , typename Ordering , typename Policies >
auto	evaluate (const ContextPolynomial< Coeff, Ordering, Policies > &p, const Assignment< typename ContextPolynomial< Coeff, Ordering, Policies >::RootType > &a)
template<typename Coeff , typename Ordering , typename Policies >
auto	evaluate (const BasicConstraint< ContextPolynomial< Coeff, Ordering, Policies >> &p, const Assignment< typename ContextPolynomial< Coeff, Ordering, Policies >::RootType > &a)
template<typename Number >
Number	branching_point (const IntRepRealAlgebraicNumber< Number > &n)
template<typename Number >
Number	sample_above (const IntRepRealAlgebraicNumber< Number > &n)
template<typename Number >
Number	sample_below (const IntRepRealAlgebraicNumber< Number > &n)
template<typename Number >
Number	sample_between (const IntRepRealAlgebraicNumber< Number > &lower, const IntRepRealAlgebraicNumber< Number > &upper)
template<typename Number >
Number	sample_between (const IntRepRealAlgebraicNumber< Number > &lower, const Number &upper)
template<typename Number >
Number	sample_between (const Number &lower, const IntRepRealAlgebraicNumber< Number > &upper)
template<typename Number >
Number	floor (const IntRepRealAlgebraicNumber< Number > &n)
template<typename Number >
Number	ceil (const IntRepRealAlgebraicNumber< Number > &n)
template<typename Number >
bool	is_zero (const IntRepRealAlgebraicNumber< Number > &n)
template<typename Number >
bool	is_integer (const IntRepRealAlgebraicNumber< Number > &n)
template<typename Number >
Number	integer_below (const IntRepRealAlgebraicNumber< Number > &n)
template<typename Number >
static IntRepRealAlgebraicNumber< Number >	abs (const IntRepRealAlgebraicNumber< Number > &n)
template<typename Number >
std::size_t	bitsize (const IntRepRealAlgebraicNumber< Number > &n)
template<typename Number >
Sign	sgn (const IntRepRealAlgebraicNumber< Number > &n)
template<typename Number >
Sign	sgn (const IntRepRealAlgebraicNumber< Number > &n, const UnivariatePolynomial< Number > &p)
template<typename Number >
bool	contained_in (const IntRepRealAlgebraicNumber< Number > &n, const Interval< Number > &i)
template<typename Number >
bool	compare (const IntRepRealAlgebraicNumber< Number > &lhs, const IntRepRealAlgebraicNumber< Number > &rhs, const Relation relation)
template<typename Number >
bool	compare (const IntRepRealAlgebraicNumber< Number > &lhs, const Number &rhs, const Relation relation)
template<typename Num >
std::ostream &	operator<< (std::ostream &os, const IntRepRealAlgebraicNumber< Num > &ran)
template<typename Coeff , typename Number = typename UnderlyingNumberType<Coeff>::type, EnableIf< std::is_same< Coeff, Number >> = dummy>
RealRootsResult< IntRepRealAlgebraicNumber< Number > >	real_roots (const UnivariatePolynomial< Coeff > &polynomial, const Interval< Number > &interval=Interval< Number >::unbounded_interval())
	Find all real roots of a univariate 'polynomial' with numeric coefficients within a given 'interval'. More...
template<typename Coeff , typename Number >
RealRootsResult< IntRepRealAlgebraicNumber< Number > >	real_roots (const UnivariatePolynomial< Coeff > &poly, const Assignment< IntRepRealAlgebraicNumber< Number >> &varToRANMap, const Interval< Number > &interval=Interval< Number >::unbounded_interval())
	Replace all variables except one of the multivariate polynomial 'p' by numbers as given in the mapping 'm', which creates a univariate polynomial, and return all roots of that created polynomial. More...
template<typename Coeff , typename Ordering , typename Policies >
auto	real_roots (const ContextPolynomial< Coeff, Ordering, Policies > &p, const Assignment< typename ContextPolynomial< Coeff, Ordering, Policies >::RootType > &a)
template<typename Number >
Number	branching_point (const RealAlgebraicNumberThom< Number > &n)
template<typename Number >
Number	evaluate (const MultivariatePolynomial< Number > &p, std::map< Variable, RealAlgebraicNumberThom< Number >> &m)
template<typename Number , typename Poly >
bool	evaluate (const BasicConstraint< Poly > &c, std::map< Variable, RealAlgebraicNumberThom< Number >> &m)
template<typename Number >
RealAlgebraicNumberThom< Number >	abs (const RealAlgebraicNumberThom< Number > &n)
template<typename Number >
RealAlgebraicNumberThom< Number >	sample_above (const RealAlgebraicNumberThom< Number > &n)
template<typename Number >
RealAlgebraicNumberThom< Number >	sample_below (const RealAlgebraicNumberThom< Number > &n)
template<typename Number >
RealAlgebraicNumberThom< Number >	sample_between (const RealAlgebraicNumberThom< Number > &lower, const RealAlgebraicNumberThom< Number > &upper)
template<typename Number >
Number	sample_between (const RealAlgebraicNumberThom< Number > &lower, const Number &upper)
template<typename Number >
Number	sample_between (const Number &lower, const RealAlgebraicNumberThom< Number > &upper)
template<typename Number >
Number	floor (const RealAlgebraicNumberThom< Number > &n)
template<typename Number >
Number	ceil (const RealAlgebraicNumberThom< Number > &n)
template<typename Number >
bool	operator== (const RealAlgebraicNumberThom< Number > &lhs, const RealAlgebraicNumberThom< Number > &rhs)
template<typename Number >
bool	operator== (const RealAlgebraicNumberThom< Number > &lhs, const Number &rhs)
template<typename Number >
bool	operator== (const Number &lhs, const RealAlgebraicNumberThom< Number > &rhs)
template<typename Number >
bool	operator< (const RealAlgebraicNumberThom< Number > &lhs, const RealAlgebraicNumberThom< Number > &rhs)
template<typename Number >
bool	operator< (const RealAlgebraicNumberThom< Number > &lhs, const Number &rhs)
template<typename Number >
bool	operator< (const Number &lhs, const RealAlgebraicNumberThom< Number > &rhs)
template<typename Num >
std::ostream &	operator<< (std::ostream &os, const RealAlgebraicNumberThom< Num > &rhs)
template<typename N >
std::ostream &	operator<< (std::ostream &os, const SignDetermination< N > &rhs)
template<typename Coeff >
std::vector< Coeff >	newtonSums (const std::vector< Coeff > &newtonSums)
template<typename Coeff >
void	printMatrix (const CoeffMatrix< Coeff > &m)
template<typename Coeff >
std::vector< Coeff >	charPol (const CoeffMatrix< Coeff > &m)
template<typename C >
std::ostream &	operator<< (std::ostream &o, const MultiplicationTable< C > &table)
template<typename Number >
int	multivariateTarskiQuery (const MultivariatePolynomial< Number > &Q, const MultiplicationTable< Number > &table)
template<typename Number >
Sign	signAtMinusInf (const UnivariatePolynomial< Number > &p)
template<typename Number >
Sign	signAtPlusInf (const UnivariatePolynomial< Number > &p)
template<typename Number >
int	univariateTarskiQuery (const UnivariatePolynomial< Number > &p, const UnivariatePolynomial< Number > &q, const UnivariatePolynomial< Number > &der_q)
template<typename Number >
int	univariateTarskiQuery (const UnivariatePolynomial< Number > &p, const UnivariatePolynomial< Number > &q)
template<typename N >
bool	operator< (const ThomEncoding< N > &lhs, const ThomEncoding< N > &rhs)
template<typename N >
bool	operator<= (const ThomEncoding< N > &lhs, const ThomEncoding< N > &rhs)
template<typename N >
bool	operator> (const ThomEncoding< N > &lhs, const ThomEncoding< N > &rhs)
template<typename N >
bool	operator>= (const ThomEncoding< N > &lhs, const ThomEncoding< N > &rhs)
template<typename N >
bool	operator== (const ThomEncoding< N > &lhs, const ThomEncoding< N > &rhs)
template<typename N >
bool	operator!= (const ThomEncoding< N > &lhs, const ThomEncoding< N > &rhs)
template<typename N >
bool	operator< (const ThomEncoding< N > &lhs, const N &rhs)
template<typename N >
bool	operator<= (const ThomEncoding< N > &lhs, const N &rhs)
template<typename N >
bool	operator> (const ThomEncoding< N > &lhs, const N &rhs)
template<typename N >
bool	operator>= (const ThomEncoding< N > &lhs, const N &rhs)
template<typename N >
bool	operator== (const ThomEncoding< N > &lhs, const N &rhs)
template<typename N >
bool	operator!= (const ThomEncoding< N > &lhs, const N &rhs)
template<typename N >
bool	operator< (const N &lhs, const ThomEncoding< N > &rhs)
template<typename N >
bool	operator<= (const N &lhs, const ThomEncoding< N > &rhs)
template<typename N >
bool	operator> (const N &lhs, const ThomEncoding< N > &rhs)
template<typename N >
bool	operator>= (const N &lhs, const ThomEncoding< N > &rhs)
template<typename N >
bool	operator== (const N &lhs, const ThomEncoding< N > &rhs)
template<typename N >
bool	operator!= (const N &lhs, const ThomEncoding< N > &rhs)
template<typename N >
ThomEncoding< N >	operator+ (const N &lhs, const ThomEncoding< N > &rhs)
template<typename N >
std::ostream &	operator<< (std::ostream &os, const ThomEncoding< N > &rhs)
template<typename Number >
RealAlgebraicNumber< Number >	evaluateTE (const MultivariatePolynomial< Number > &p, std::map< Variable, RealAlgebraicNumber< Number >> &m)
template<typename Number >
std::list< ThomEncoding< Number > >	realRootsThom (const MultivariatePolynomial< Number > &p, Variable::Arg mainVar, std::shared_ptr< ThomEncoding< Number >> point_ptr, const Interval< Number > &interval=Interval< Number >::unbounded_interval())
template<typename Number >
std::list< ThomEncoding< Number > >	realRootsThom (const MultivariatePolynomial< Number > &p, Variable::Arg mainVar, const std::map< Variable, ThomEncoding< Number >> &m={}, const Interval< Number > &interval=Interval< Number >::unbounded_interval())
template<typename Coeff , typename Number >
std::list< RealAlgebraicNumber< Number > >	realRootsThom (const UnivariatePolynomial< Coeff > &p, const std::map< Variable, RealAlgebraicNumber< Number >> &m, const Interval< Number > &interval)
template<typename Number >
std::list< MultivariatePolynomial< Number > >	der (const MultivariatePolynomial< Number > &p, Variable::Arg var, uint from, uint upto)
template<typename Poly >
std::pair< typename SqrtEx< Poly >::Rational, bool >	evaluate (const SqrtEx< Poly > &sqrt_ex, const std::map< Variable, typename SqrtEx< Poly >::Rational > &eval_map, int rounding)
	Evaluates the square root expression. More...
template<typename Poly >
void	variables (const SqrtEx< Poly > &ex, carlVariables &vars)
template<typename Poly >
SqrtEx< Poly >	substitute (const SqrtEx< Poly > &sqrt_ex, const std::map< Variable, typename SqrtEx< Poly >::Rational > &eval_map)
template<typename Poly >
SqrtEx< Poly >	substitute (const Poly &_substituteIn, const carl::Variable _varToSubstitute, const SqrtEx< Poly > &_substituteBy)
	Substitutes a variable in an expression by a square root expression, which results in a square root expression. More...
std::ostream &	operator<< (std::ostream &os, CMakeOptionPrinter cmop)
constexpr CMakeOptionPrinter	CMakeOptions (bool advanced=false) noexcept
BitVector	operator| (const BitVector &lhs, const BitVector &rhs)
bool	operator== (const BitVector &lhs, const BitVector &rhs)
bool	operator== (const BitVector::forward_iterator &fi1, const BitVector::forward_iterator &fi2)
std::ostream &	operator<< (std::ostream &os, const BitVector &bv)
template<typename TT >
std::ostream &	operator<< (std::ostream &os, const tree< TT > &tree)
template<class E , bool FI>
std::ostream &	operator<< (std::ostream &out, const CompactTree< E, FI > &tree)
std::string	demangle (const char *name)
void	printStacktrace ()
	Uses GDB to print a stack trace. More...
std::string	callingFunction ()
static void	handle_signal (int signal)
	Actual signal handler. More...
static bool	install_signal_handler () noexcept
	Installs the signal handler. More...
template<typename T >
std::string	typeString ()
std::ostream &	operator<< (std::ostream &os, const Timer &t)
	Streaming operator for a Timer. More...
template<typename T , class I >
bool	operator== (const TypeInfoPair< T, I > &_tipA, const TypeInfoPair< T, I > &_tipB)
template<typename T >
bool	returnFalse (const T &, const T &)
template<typename T >
void	doNothing (const T &, const T &)
template<class... Ts>
	overloaded (Ts...) -> overloaded< Ts... >
	has_method_struct (normalize) has_method_struct(is_negative) has_method_struct(is_positive) has_function_overload(is_one) has_function_overload(is_zero) template< template< typename... > class Template
template<typename Enum >
constexpr Enum	invalid_enum_value ()
	Returns an enum value that is (most probably) not a valid enum value. More...
template<typename Enum >
constexpr auto	underlying_enum_value (Enum e)
	Casts an enum value to a value of the underlying number type. More...
void	hash_combine (std::size_t &seed, std::size_t value)
	Add a value to the given hash seed. More...
template<typename T >
void	hash_add (std::size_t &seed, const T &value)
	Add hash of the given value to the hash seed. More...
template<>
void	hash_add (std::size_t &seed, const std::size_t &value)
	Add hash of the given value to the hash seed. More...
template<typename T1 , typename T2 >
void	hash_add (std::size_t &seed, const std::pair< T1, T2 > &p)
	Add hash of both elements of a std::pair to the seed. More...
template<typename T >
void	hash_add (std::size_t &seed, const std::vector< T > &v)
	Add hash of all elements of a std::vector to the seed. More...
template<typename T >
void	hash_add (std::size_t &seed, const std::set< T > &s)
template<typename First , typename... Tail>
void	hash_add (std::size_t &seed, const First &value, Tail &&... tail)
	Variadic version of hash_add to add an arbitrary number of values to the seed. More...
template<typename... Args>
std::size_t	hash_all (Args &&... args)
	Hashes an arbitrary number of values. More...
template<typename T >
std::ostream &	operator<< (std::ostream &os, const std::forward_list< T > &l)
	Output a std::forward_list with arbitrary content. More...
template<typename T >
std::ostream &	operator<< (std::ostream &os, const std::initializer_list< T > &l)
	Output a std::initializer_list with arbitrary content. More...
template<typename T >
std::ostream &	operator<< (std::ostream &os, const std::list< T > &l)
	Output a std::list with arbitrary content. More...
template<typename Key , typename Value , typename Comparator >
std::ostream &	operator<< (std::ostream &os, const std::map< Key, Value, Comparator > &m)
	Output a std::map with arbitrary content. More...
template<typename Key , typename Value , typename Comparator >
std::ostream &	operator<< (std::ostream &os, const std::multimap< Key, Value, Comparator > &m)
	Output a std::multimap with arbitrary content. More...
template<typename T >
std::ostream &	operator<< (std::ostream &os, const std::optional< T > &o)
	Output a std::optional with arbitrary content. More...
template<typename U , typename V >
std::ostream &	operator<< (std::ostream &os, const std::pair< U, V > &p)
	Output a std::pair with arbitrary content. More...
template<typename T , typename C >
std::ostream &	operator<< (std::ostream &os, const std::set< T, C > &s)
	Output a std::set with arbitrary content. More...
template<typename... T>
std::ostream &	operator<< (std::ostream &os, const std::tuple< T... > &t)
	Output a std::tuple with arbitrary content. More...
template<typename Key , typename Value , typename H , typename E , typename A >
std::ostream &	operator<< (std::ostream &os, const std::unordered_map< Key, Value, H, E, A > &m)
	Output a std::unordered_map with arbitrary content. More...
template<typename T , typename H , typename K , typename A >
std::ostream &	operator<< (std::ostream &os, const std::unordered_set< T, H, K, A > &s)
	Output a std::unordered_set with arbitrary content. More...
template<typename T , typename... Tail>
std::ostream &	operator<< (std::ostream &os, const std::variant< T, Tail... > &v)
	Output a std::variant with arbitrary content. More...
template<typename T >
std::ostream &	operator<< (std::ostream &os, const std::vector< T > &v)
	Output a std::vector with arbitrary content. More...
template<typename T >
std::ostream &	operator<< (std::ostream &os, const std::deque< T > &v)
	Output a std::deque with arbitrary content. More...
template<typename T >
auto	stream_joined (const std::string &glue, const T &v)
	Allows to easily output some container with all elements separated by some string. More...
template<typename T , typename F >
auto	stream_joined (const std::string &glue, const T &v, F &&f)
	Allows to easily output some container with all elements separated by some string. More...
template<typename T , typename C >
std::ostream &	operator<< (std::ostream &os, const boost::container::flat_set< T, C > &s)
	Output a boost::container::flat_set with arbitrary content. More...
template<class Key , class T , class Compare , class AllocatorOrContainer >
std::ostream &	operator<< (std::ostream &os, const boost::container::flat_map< Key, T, Compare, AllocatorOrContainer > &m)
	Output a boost::container::flat_map with arbitrary content. More...
template<typename Tuple1 , typename Tuple2 >
auto	tuple_cat (Tuple1 &&t1, Tuple2 &&t2)
template<typename Tuple >
auto	tuple_tail (Tuple &&t)
	Returns a new tuple containing everything but the first element. More...
template<typename F , typename Tuple >
auto	tuple_apply (F &&f, Tuple &&t)
	Invokes a callable object f on a tuple of arguments. More...
template<typename F , typename Tuple >
auto	tuple_foreach (F &&f, Tuple &&t)
	Invokes a callable object f on every element of a tuple and returns a tuple containing the results. More...
template<typename Tuple , typename T , typename F >
T	tuple_accumulate (Tuple &&t, T &&init, F &&f)
	Implements a functional fold (similar to std::accumulate) for std::tuple. More...
template<typename T , typename Variant >
bool	variant_is_type (const Variant &variant) noexcept
	Checks whether a variant contains a value of a fiven type. More...
template<typename Target , typename... Args>
Target	variant_extend (const boost::variant< Args... > &variant)
template<typename... T>
std::size_t	variant_hash (const boost::variant< T... > &value)
template<typename Coeff , typename Subst >
Subst	evaluate (const FactorizedPolynomial< Coeff > &p, const std::map< Variable, Subst > &substitutions)
	Like substitute, but expects substitutions for all variables. More...
template<typename P , typename Numeric >
Interval< Numeric >	evaluate (const FactorizedPolynomial< P > &p, const std::map< Variable, Interval< Numeric >> &map)
template<typename P >
bool	is_one (const FactorizedPolynomial< P > &fp)
template<typename P >
bool	is_zero (const FactorizedPolynomial< P > &fp)
template<typename P >
P	computePolynomial (const FactorizedPolynomial< P > &_fpoly)
	Obtains the polynomial (representation) of this factorized polynomial. More...
template<typename P >
std::ostream &	operator<< (std::ostream &_out, const FactorizedPolynomial< P > &_fpoly)
	Prints the factorization representation of the given factorized polynomial on the given output stream. More...
template<typename P >
std::string	factorizationToString (const Factorization< P > &_factorization, bool _infix=true, bool _friendlyVarNames=true)
template<typename P >
std::ostream &	operator<< (std::ostream &_out, const Factorization< P > &_factorization)
template<typename P >
bool	factorizationsEqual (const Factorization< P > &_factorizationA, const Factorization< P > &_factorizationB)
template<typename P >
P	computePolynomial (const PolynomialFactorizationPair< P > &_pfPair)
	Compute the polynomial from the given polynomial-factorization pair. More...
template<typename Pol , bool AS>
RationalFunction< Pol, AS >	operator+ (const RationalFunction< Pol, AS > &lhs, const RationalFunction< Pol, AS > &rhs)
template<typename Pol , bool AS>
RationalFunction< Pol, AS >	operator+ (const RationalFunction< Pol, AS > &lhs, const Pol &rhs)
template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>
RationalFunction< Pol, AS >	operator+ (const RationalFunction< Pol, AS > &lhs, const Term< typename Pol::CoeffType > &rhs)
template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>
RationalFunction< Pol, AS >	operator+ (const RationalFunction< Pol, AS > &lhs, const Monomial::Arg &rhs)
template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>
RationalFunction< Pol, AS >	operator+ (const RationalFunction< Pol, AS > &lhs, Variable rhs)
template<typename Pol , bool AS>
RationalFunction< Pol, AS >	operator+ (const RationalFunction< Pol, AS > &lhs, const typename Pol::CoeffType &rhs)
template<typename Pol , bool AS>
RationalFunction< Pol, AS >	operator- (const RationalFunction< Pol, AS > &lhs)
template<typename Pol , bool AS>
RationalFunction< Pol, AS >	operator- (const RationalFunction< Pol, AS > &lhs, const RationalFunction< Pol, AS > &rhs)
template<typename Pol , bool AS>
RationalFunction< Pol, AS >	operator- (const RationalFunction< Pol, AS > &lhs, const Pol &rhs)
template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>
RationalFunction< Pol, AS >	operator- (const RationalFunction< Pol, AS > &lhs, const Term< typename Pol::CoeffType > &rhs)
template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>
RationalFunction< Pol, AS >	operator- (const RationalFunction< Pol, AS > &lhs, const Monomial::Arg &rhs)
template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>
RationalFunction< Pol, AS >	operator- (const RationalFunction< Pol, AS > &lhs, Variable rhs)
template<typename Pol , bool AS>
RationalFunction< Pol, AS >	operator- (const RationalFunction< Pol, AS > &lhs, const typename Pol::CoeffType &rhs)
template<typename Pol , bool AS>
RationalFunction< Pol, AS >	operator* (const RationalFunction< Pol, AS > &lhs, const RationalFunction< Pol, AS > &rhs)
template<typename Pol , bool AS>
RationalFunction< Pol, AS >	operator* (const RationalFunction< Pol, AS > &lhs, const Pol &rhs)
template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>
RationalFunction< Pol, AS >	operator* (const RationalFunction< Pol, AS > &lhs, const Term< typename Pol::CoeffType > &rhs)
template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>
RationalFunction< Pol, AS >	operator* (const RationalFunction< Pol, AS > &lhs, const Monomial::Arg &rhs)
template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>
RationalFunction< Pol, AS >	operator* (const RationalFunction< Pol, AS > &lhs, Variable rhs)
template<typename Pol , bool AS>
RationalFunction< Pol, AS >	operator* (const RationalFunction< Pol, AS > &lhs, const typename Pol::CoeffType &rhs)
template<typename Pol , bool AS>
RationalFunction< Pol, AS >	operator* (const typename Pol::CoeffType &lhs, const RationalFunction< Pol, AS > &rhs)
template<typename Pol , bool AS>
RationalFunction< Pol, AS >	operator* (const RationalFunction< Pol, AS > &lhs, carl::sint rhs)
template<typename Pol , bool AS>
RationalFunction< Pol, AS >	operator* (carl::sint lhs, const RationalFunction< Pol, AS > &rhs)
template<typename Pol , bool AS>
RationalFunction< Pol, AS >	operator/ (const RationalFunction< Pol, AS > &lhs, const RationalFunction< Pol, AS > &rhs)
template<typename Pol , bool AS>
RationalFunction< Pol, AS >	operator/ (const RationalFunction< Pol, AS > &lhs, const Pol &rhs)
template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>
RationalFunction< Pol, AS >	operator/ (const RationalFunction< Pol, AS > &lhs, const Term< typename Pol::CoeffType > &rhs)
template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>
RationalFunction< Pol, AS >	operator/ (const RationalFunction< Pol, AS > &lhs, const Monomial::Arg &rhs)
template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>
RationalFunction< Pol, AS >	operator/ (const RationalFunction< Pol, AS > &lhs, Variable rhs)
template<typename Pol , bool AS>
RationalFunction< Pol, AS >	operator/ (const RationalFunction< Pol, AS > &lhs, const typename Pol::CoeffType &rhs)
template<typename Pol , bool AS>
RationalFunction< Pol, AS >	operator/ (const RationalFunction< Pol, AS > &lhs, unsigned long rhs)
template<typename Pol , bool AS>
RationalFunction< Pol, AS >	pow (unsigned exp, const RationalFunction< Pol, AS > &rf)
template<typename Pol , bool AS>
bool	operator!= (const RationalFunction< Pol, AS > &lhs, const RationalFunction< Pol, AS > &rhs)
template<typename P >
FactorizedPolynomial< P >	substitute (const FactorizedPolynomial< P > &p, Variable var, const FactorizedPolynomial< P > &value)
	Replace the given variable by the given value. More...
template<typename P >
FactorizedPolynomial< P >	substitute (const FactorizedPolynomial< P > &p, const std::map< Variable, FactorizedPolynomial< P >> &substitutions)
	Replace all variables by a value given in their map. More...
template<typename P >
FactorizedPolynomial< P >	substitute (const FactorizedPolynomial< P > &p, const std::map< Variable, FactorizedPolynomial< P >> &substitutions, const std::map< Variable, P > &substitutionsAsP)
	Replace all variables by a value given in their map. More...
template<typename P , typename Subs >
FactorizedPolynomial< P >	substitute (const FactorizedPolynomial< P > &p, const std::map< Variable, Subs > &substitutions)
	Replace all variables by a value given in their map. More...
template<typename P >
bool	operator== (const Constraint< P > &lhs, const Constraint< P > &rhs)
template<typename P >
bool	operator!= (const Constraint< P > &lhs, const Constraint< P > &rhs)
template<typename P >
bool	operator< (const Constraint< P > &lhs, const Constraint< P > &rhs)
template<typename P >
bool	operator<= (const Constraint< P > &lhs, const Constraint< P > &rhs)
template<typename P >
bool	operator> (const Constraint< P > &lhs, const Constraint< P > &rhs)
template<typename P >
bool	operator>= (const Constraint< P > &lhs, const Constraint< P > &rhs)
template<typename Poly >
std::ostream &	operator<< (std::ostream &os, const Constraint< Poly > &c)
	Prints the given constraint on the given stream. More...
template<typename Pol >
void	variables (const Constraint< Pol > &c, carlVariables &vars)
template<typename Pol >
std::optional< std::pair< Variable, Pol > >	get_substitution (const Constraint< Pol > &c, bool _negated=false, Variable _exclude=carl::Variable::NO_VARIABLE)
template<typename Pol >
auto	get_assignment (const Constraint< Pol > &c)
template<typename Pol >
auto	compare (const Constraint< Pol > &c1, const Constraint< Pol > &c2)
template<typename Pol >
auto	satisfied_by (const Constraint< Pol > &c, const Assignment< typename Pol::NumberType > &a)
template<typename Pol >
bool	is_bound (const Constraint< Pol > &constr, bool negated=false)
template<typename Pol >
bool	is_lower_bound (const Constraint< Pol > &constr)
template<typename Pol >
bool	is_upper_bound (const Constraint< Pol > &constr)
std::string	toString (BVCompareRelation _r)
std::ostream &	operator<< (std::ostream &_os, const BVCompareRelation &_r)
std::size_t	toId (const BVCompareRelation _relation)
BVCompareRelation	inverse (BVCompareRelation _c)
bool	relationIsStrict (BVCompareRelation _r)
bool	relationIsSigned (BVCompareRelation _r)
bool	operator== (const BVConstraint &lhs, const BVConstraint &rhs)
bool	operator< (const BVConstraint &lhs, const BVConstraint &rhs)
std::ostream &	operator<< (std::ostream &os, const BVConstraint &c)
bool	operator== (const BVTerm &lhs, const BVTerm &rhs)
bool	operator< (const BVTerm &lhs, const BVTerm &rhs)
std::ostream &	operator<< (std::ostream &os, const BVTerm &term)
bool	operator== (const BVTermContent &lhs, const BVTermContent &rhs)
bool	operator< (const BVTermContent &lhs, const BVTermContent &rhs)
std::ostream &	operator<< (std::ostream &os, const BVTermContent &term)
	The output operator of a term. More...
auto	typeId (BVTermType type)
std::ostream &	operator<< (std::ostream &os, BVTermType type)
bool	typeIsUnary (BVTermType type)
bool	typeIsBinary (BVTermType type)
BVValue	operator+ (const BVValue &lhs, const BVValue &rhs)
BVValue	operator* (const BVValue &lhs, const BVValue &rhs)
bool	operator== (const BVValue &lhs, const BVValue &rhs)
bool	operator< (const BVValue &lhs, const BVValue &rhs)
BVValue	operator~ (const BVValue &val)
BVValue	operator- (const BVValue &val)
BVValue	operator- (const BVValue &lhs, const BVValue &rhs)
BVValue	operator% (const BVValue &lhs, const BVValue &rhs)
BVValue	operator/ (const BVValue &lhs, const BVValue &rhs)
BVValue	operator& (const BVValue &lhs, const BVValue &rhs)
BVValue	operator| (const BVValue &lhs, const BVValue &rhs)
BVValue	operator^ (const BVValue &lhs, const BVValue &rhs)
BVValue	operator<< (const BVValue &lhs, const BVValue &rhs)
BVValue	operator>> (const BVValue &lhs, const BVValue &rhs)
std::ostream &	operator<< (std::ostream &os, const BVValue &val)
bool	operator== (const BVVariable &lhs, const BVVariable &rhs)
bool	operator== (const BVVariable &lhs, const Variable &rhs)
bool	operator== (const Variable &lhs, const BVVariable &rhs)
bool	operator< (const BVVariable &lhs, const BVVariable &rhs)
bool	operator< (const BVVariable &lhs, const Variable &rhs)
bool	operator< (const Variable &lhs, const BVVariable &rhs)
bool	operator<= (const Condition &lhs, const Condition &rhs)
	Check whether the bits of one condition are always set if the corresponding bit of another condition is set. More...
template<typename P >
std::ostream &	operator<< (std::ostream &os, const Formula< P > &f)
	The output operator of a formula. More...
std::string	formulaTypeToString (FormulaType _type)
std::ostream &	operator<< (std::ostream &os, FormulaType t)
template<typename Pol >
std::ostream &	operator<< (std::ostream &os, const FormulaContent< Pol > &f)
	The output operator of a formula. More...
template<typename Pol >
std::ostream &	operator<< (std::ostream &os, const FormulaContent< Pol > *fc)
template<typename Pol >
std::size_t	hash_value (const carl::FormulaContent< Pol > &content)
template<typename Poly >
Formula< Poly >	to_cnf (const Formula< Poly > &f, bool keep_constraints=true, bool simplify_combinations=false, bool tseitin_equivalence=true)
	Converts the given formula to CNF. More...
template<typename Pol >
size_t	complexity (const Formula< Pol > &f)
template<typename Pol >
Formula< Pol >	addConstraintBound (ConstraintBounds< Pol > &_constraintBounds, const Formula< Pol > &_constraint, bool _inConjunction)
	Adds the bound to the bounds of the polynomial specified by this constraint. More...
template<typename Pol >
bool	swapConstraintBounds (ConstraintBounds< Pol > &_constraintBounds, Formulas< Pol > &_intoFormulas, bool _inConjunction)
	Stores for every polynomial for which we determined bounds for given constraints a minimal set of constraints representing these bounds into the given set of sub-formulas of a conjunction (_inConjunction == true) or disjunction (_inConjunction == false) to construct. More...
template<typename Pol >
Formula< Pol >	resolve_negation (const Formula< Pol > &f, bool _keepConstraint=true, bool resolve_varcomp=false)
	Resolves the outermost negation of this formula. More...
template<typename Poly >
Formula< Poly >	to_nnf (const Formula< Poly > &formula)
std::ostream &	operator<< (std::ostream &os, const Quantifier &type)
template<typename Poly >
Formula< Poly >	to_pnf (const Formula< Poly > &f, QuantifierPrefix &prefix, boost::container::flat_set< Variable > &used_vars, bool negated=false)
template<typename Poly >
void	free_variables (const Formula< Poly > &f, boost::container::flat_set< Variable > &current_quantified_vars, boost::container::flat_set< Variable > &free_vars)
template<typename Poly >
auto	free_variables (const Formula< Poly > &f)
template<typename Poly >
std::pair< QuantifierPrefix, Formula< Poly > >	to_pnf (const Formula< Poly > &f)
	Transforms this formula to its equivalent in prenex normal form. More...
template<typename Poly >
Formula< Poly >	to_formula (const QuantifierPrefix &prefix, const Formula< Poly > &matrix)
template<typename Pol , typename Source , typename Target >
Formula< Pol >	substitute (const Formula< Pol > &formula, const Source &source, const Target &target)
template<typename Pol >
Formula< Pol >	substitute (const Formula< Pol > &formula, const std::map< Formula< Pol >, Formula< Pol >> &replacements)
template<typename Pol >
Formula< Pol >	substitute (const Formula< Pol > &formula, const std::map< Variable, typename Formula< Pol >::PolynomialType > &replacements)
template<typename Pol >
Formula< Pol >	substitute (const Formula< Pol > &formula, const std::map< BVVariable, BVTerm > &replacements)
template<typename Pol >
Formula< Pol >	substitute (const Formula< Pol > &formula, const std::map< UVariable, UFInstance > &replacements)
template<typename Pol >
void	variables (const Formula< Pol > &f, carlVariables &vars)
template<typename Pol >
void	uninterpreted_functions (const Formula< Pol > &f, std::set< UninterpretedFunction > &ufs)
template<typename Pol >
void	uninterpreted_variables (const Formula< Pol > &f, std::set< UVariable > &uvs)
template<typename Pol >
void	bitvector_variables (const Formula< Pol > &f, std::set< BVVariable > &bvvs)
template<typename Pol >
void	arithmetic_constraints (const Formula< Pol > &f, std::vector< Constraint< Pol >> &constraints)
	Collects all constraint occurring in this formula. More...
template<typename Pol >
void	arithmetic_constraints (const Formula< Pol > &f, std::vector< Formula< Pol >> &constraints)
	Collects all constraint occurring in this formula. More...
template<typename Pol , typename Visitor >
void	visit (const Formula< Pol > &formula, Visitor func)
	Recursively calls func on every subformula. More...
template<typename Pol , typename Visitor >
Formula< Pol >	visit_result (const Formula< Pol > &formula, Visitor func)
	Recursively calls func on every subformula and return a new formula. More...
std::ostream &	operator<< (std::ostream &os, const Logic &l)
template<typename Rational , typename Poly >
bool	getRationalAssignmentsFromModel (const Model< Rational, Poly > &_model, std::map< Variable, Rational > &_rationalAssigns)
	Obtains all assignments which can be transformed to rationals and stores them in the passed map. More...
template<typename Rational , typename Poly >
unsigned	satisfies (const Model< Rational, Poly > &_assignment, const Formula< Poly > &_formula)
template<typename Rational , typename Poly >
bool	isPartOf (const std::map< Variable, Rational > &_assignment, const Model< Rational, Poly > &_model)
template<typename Rational , typename Poly >
unsigned	satisfies (const Model< Rational, Poly > &_model, const std::map< Variable, Rational > &_assignment, const std::map< BVVariable, BVTerm > &bvAssigns, const Formula< Poly > &_formula)
template<typename Rational , typename Poly >
void	getDefaultModel (Model< Rational, Poly > &_defaultModel, const UEquality &_constraint, bool _overwrite=true, size_t _seed=0)
template<typename Rational , typename Poly >
void	getDefaultModel (Model< Rational, Poly > &_defaultModel, const BVTerm &_constraint, bool _overwrite=true, size_t _seed=0)
template<typename Rational , typename Poly >
void	getDefaultModel (Model< Rational, Poly > &_defaultModel, const Constraint< Poly > &_constraint, bool _overwrite=true, size_t _seed=0)
template<typename Rational , typename Poly >
void	getDefaultModel (Model< Rational, Poly > &_defaultModel, const Formula< Poly > &_formula, bool _overwrite=true, size_t _seed=0)
template<typename Rational , typename Poly >
Formula< Poly >	representingFormula (const ModelVariable &mv, const Model< Rational, Poly > &model)
template<typename Rational , typename Poly >
std::optional< Assignment< typename Poly::RootType > >	get_ran_assignment (const carlVariables &vars, const Model< Rational, Poly > &model)
template<typename Rational , typename Poly >
Assignment< typename Poly::RootType >	get_ran_assignment (const Model< Rational, Poly > &model)
template<typename T , typename Rational , typename Poly >
T	substitute (const T &t, const Model< Rational, Poly > &m)
	Substitutes a model into an expression t. More...
template<typename T , typename Rational , typename Poly >
ModelValue< Rational, Poly >	evaluate (const T &t, const Model< Rational, Poly > &m)
	Evaluates a given expression t over a model. More...
template<typename T , typename Rational , typename Poly >
unsigned	satisfied_by (const T &t, const Model< Rational, Poly > &m)
template<typename Rational , typename Poly >
void	substitute_inplace (BVTerm &bvt, const Model< Rational, Poly > &m)
	Substitutes all variables from a model within a bitvector term. More...
template<typename Rational , typename Poly >
void	substitute_inplace (BVConstraint &bvc, const Model< Rational, Poly > &m)
	Substitutes all variables from a model within a bitvector constraint. More...
template<typename Rational , typename Poly >
void	evaluate_inplace (ModelValue< Rational, Poly > &res, BVTerm &bvt, const Model< Rational, Poly > &m)
	Evaluates a bitvector term to a ModelValue over a Model. More...
template<typename Rational , typename Poly >
void	evaluate_inplace (ModelValue< Rational, Poly > &res, BVConstraint &bvc, const Model< Rational, Poly > &m)
	Evaluates a bitvector constraint to a ModelValue over a Model. More...
template<typename Rational , typename Poly >
void	substitute_inplace (Constraint< Poly > &c, const Model< Rational, Poly > &m)
	Substitutes all variables from a model within a constraint. More...
template<typename Rational , typename Poly >
void	evaluate_inplace (ModelValue< Rational, Poly > &res, Constraint< Poly > &c, const Model< Rational, Poly > &m)
	Evaluates a constraint to a ModelValue over a Model. More...
template<typename Rational , typename Poly >
void	substitute_inplace (Formula< Poly > &f, const Model< Rational, Poly > &m)
	Substitutes all variables from a model within a formula. More...
template<typename Rational , typename Poly >
void	evaluate_inplace (ModelValue< Rational, Poly > &res, Formula< Poly > &f, const Model< Rational, Poly > &m)
	Evaluates a formula to a ModelValue over a Model. More...
template<typename Rational , typename Poly >
void	substitute_inplace (MultivariateRoot< Poly > &mvr, const Model< Rational, Poly > &m)
	Substitutes all variables from a model within a MultivariateRoot. More...
template<typename Rational , typename Poly >
void	evaluate_inplace (ModelValue< Rational, Poly > &res, MultivariateRoot< Poly > &mvr, const Model< Rational, Poly > &m)
	Evaluates a MultivariateRoot to a ModelValue over a Model. More...
template<typename Rational , typename Poly , typename ModelPoly >
void	substitute_inplace (Poly &p, const Model< Rational, ModelPoly > &m)
	Substitutes all variables from a model within a polynomial. More...
template<typename Rational , typename Poly >
void	evaluate_inplace (ModelValue< Rational, Poly > &res, Poly &p, const Model< Rational, Poly > &m)
	Evaluates a polynomial to a ModelValue over a Model. More...
template<typename Rational , typename Poly >
void	evaluate_inplace (ModelValue< Rational, Poly > &res, const UVariable &uv, const Model< Rational, Poly > &m)
	Evaluates a uninterpreted variable to a ModelValue over a Model. More...
template<typename Rational , typename Poly >
void	evaluate_inplace (ModelValue< Rational, Poly > &res, const UFInstance &ufi, const Model< Rational, Poly > &m)
	Evaluates a uninterpreted function instance to a ModelValue over a Model. More...
template<typename Rational , typename Poly >
void	evaluate_inplace (ModelValue< Rational, Poly > &res, const UEquality &ue, const Model< Rational, Poly > &m)
	Evaluates a uninterpreted variable to a ModelValue over a Model. More...
template<typename Rational , typename Poly >
std::ostream &	operator<< (std::ostream &os, const Model< Rational, Poly > &model)
template<typename Rational , typename Poly >
std::ostream &	operator<< (std::ostream &os, const ModelSubstitution< Rational, Poly > &ms)
template<typename Rational , typename Poly >
std::ostream &	operator<< (std::ostream &os, const ModelSubstitutionPtr< Rational, Poly > &ms)
template<typename Rational , typename Poly , typename Substitution , typename... Args>
ModelValue< Rational, Poly >	createSubstitution (Args &&... args)
template<typename Rational , typename Poly , typename Substitution , typename... Args>
ModelSubstitutionPtr< Rational, Poly >	createSubstitutionPtr (Args &&... args)
template<typename Rational , typename Poly >
ModelValue< Rational, Poly >	createSubstitution (const MultivariateRoot< Poly > &mr)
bool	operator== (InfinityValue lhs, InfinityValue rhs)
std::ostream &	operator<< (std::ostream &os, const InfinityValue &iv)
template<typename Rational , typename Poly >
bool	operator== (const ModelValue< Rational, Poly > &lhs, const ModelValue< Rational, Poly > &rhs)
	Check if two Assignments are equal. More...
template<typename Rational , typename Poly >
bool	operator< (const ModelValue< Rational, Poly > &lhs, const ModelValue< Rational, Poly > &rhs)
template<typename R , typename P >
std::ostream &	operator<< (std::ostream &os, const ModelValue< R, P > &mv)
bool	operator== (const ModelVariable &lhs, const ModelVariable &rhs)
	Return true if lhs is equal to rhs. More...
bool	operator< (const ModelVariable &lhs, const ModelVariable &rhs)
	Return true if lhs is smaller than rhs. More...
std::ostream &	operator<< (std::ostream &os, const ModelVariable &mv)
std::ostream &	operator<< (std::ostream &_os, const Sort &_sort)
bool	operator== (Sort lhs, Sort rhs)
bool	operator!= (Sort lhs, Sort rhs)
bool	operator< (Sort lhs, Sort rhs)
	Checks whether one sort is smaller than another. More...
bool	operator< (const SortContent &lhs, const SortContent &rhs)
template<typename... Args>
Sort	getSort (Args &&... args)
	Gets the sort specified by the arguments. More...
std::ostream &	operator<< (std::ostream &os, const SortValue &sv)
	Prints the given sort value on the given output stream. More...
bool	operator== (const SortValue &lhs, const SortValue &rhs)
	Compares two sort values for equality. More...
bool	operator< (const SortValue &lhs, const SortValue &rhs)
	Orders two sort values. More...
SortValue	newSortValue (const Sort &sort)
	Creates a new value for the given sort. More...
SortValue	defaultSortValue (const Sort &sort)
	Returns the default value for the given sort. More...
void	collectUFVars (std::set< UVariable > &uvars, UFInstance ufi)
bool	operator== (const UEquality &lhs, const UEquality &rhs)
bool	operator!= (const UEquality &lhs, const UEquality &rhs)
bool	operator< (const UEquality &lhs, const UEquality &rhs)
std::ostream &	operator<< (std::ostream &os, const UEquality &ueq)
	Prints the given uninterpreted equality on the given output stream. More...
std::ostream &	operator<< (std::ostream &os, const UFInstance &ufun)
	Prints the given uninterpreted function instance on the given output stream. More...
bool	operator== (const UFInstance &lhs, const UFInstance &rhs)
bool	operator< (const UFInstance &lhs, const UFInstance &rhs)
UFInstance	newUFInstance (const UninterpretedFunction &uf, std::vector< UTerm > &&args)
	Gets the uninterpreted function instance with the given name, domain, arguments and codomain. More...
UFInstance	newUFInstance (const UninterpretedFunction &uf, const std::vector< UTerm > &args)
	Gets the uninterpreted function instance with the given name, domain, arguments and codomain. More...
bool	operator== (const UFContent &lhs, const UFContent &rhs)
bool	operator< (const UFContent &lhs, const UFContent &rhs)
UninterpretedFunction	newUninterpretedFunction (std::string name, std::vector< Sort > domain, Sort codomain)
	Gets the uninterpreted function with the given name, domain, arguments and codomain. More...
std::ostream &	operator<< (std::ostream &os, const UFModel &ufm)
	Prints the given uninterpreted function model on the given output stream. More...
bool	operator== (const UFModel &lhs, const UFModel &rhs)
	Compares two UFModel objects for equality. More...
bool	operator< (const UFModel &lhs, const UFModel &rhs)
	Checks whether one UFModel is smaller than another. More...
bool	operator== (const UninterpretedFunction &lhs, const UninterpretedFunction &rhs)
	Check whether two uninterpreted functions are equal. More...
bool	operator< (const UninterpretedFunction &lhs, const UninterpretedFunction &rhs)
	Check whether one uninterpreted function is smaller than another. More...
std::ostream &	operator<< (std::ostream &os, const UninterpretedFunction &ufun)
	Prints the given uninterpreted function on the given output stream. More...
bool	operator== (const UTerm &lhs, const UTerm &rhs)
bool	operator!= (const UTerm &lhs, const UTerm &rhs)
bool	operator< (const UTerm &lhs, const UTerm &rhs)
std::ostream &	operator<< (std::ostream &os, const UTerm &ut)
	Prints the given uninterpreted term on the given output stream. More...
std::ostream &	operator<< (std::ostream &os, UVariable uvar)
	Prints the given uninterpreted variable on the given output stream. More...
bool	operator== (UVariable lhs, UVariable rhs)
bool	operator< (UVariable lhs, UVariable rhs)
template<typename T >
std::string	binary (const T &a, const bool &spacing=true)
	Return the binary representation given value as bit string. More...
std::string	basename (const std::string &filename)
	Return the basename of a given filename. More...
Multiplication operators
Monomial::Arg	operator* (const Monomial::Arg &lhs, const Monomial::Arg &rhs)
	Perform a multiplication involving a monomial. More...
Monomial::Arg	operator* (const Monomial::Arg &lhs, Variable rhs)
	Perform a multiplication involving a monomial. More...
Monomial::Arg	operator* (Variable lhs, const Monomial::Arg &rhs)
	Perform a multiplication involving a monomial. More...
Monomial::Arg	operator* (Variable lhs, Variable rhs)
	Perform a multiplication involving a monomial. More...
template<typename C , typename O , typename P >
auto	operator* (const MultivariatePolynomial< C, O, P > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Perform a multiplication involving a polynomial using operator*=(). More...
template<typename C , typename O , typename P >
auto	operator* (const MultivariatePolynomial< C, O, P > &lhs, const Term< C > &rhs)
	Perform a multiplication involving a polynomial using operator*=(). More...
template<typename C , typename O , typename P >
auto	operator* (const MultivariatePolynomial< C, O, P > &lhs, const Monomial::Arg &rhs)
	Perform a multiplication involving a polynomial using operator*=(). More...
template<typename C , typename O , typename P >
auto	operator* (const MultivariatePolynomial< C, O, P > &lhs, Variable rhs)
	Perform a multiplication involving a polynomial using operator*=(). More...
template<typename C , typename O , typename P >
auto	operator* (const MultivariatePolynomial< C, O, P > &lhs, const C &rhs)
	Perform a multiplication involving a polynomial using operator*=(). More...
template<typename C , typename O , typename P >
auto	operator* (const Term< C > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Perform a multiplication involving a polynomial using operator*=(). More...
template<typename C , typename O , typename P >
auto	operator* (const Monomial::Arg &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Perform a multiplication involving a polynomial using operator*=(). More...
template<typename C , typename O , typename P >
auto	operator* (Variable lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Perform a multiplication involving a polynomial using operator*=(). More...
template<typename C , typename O , typename P >
auto	operator* (const C &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Perform a multiplication involving a polynomial using operator*=(). More...
template<typename Coeff >
Term< Coeff >	operator* (Term< Coeff > lhs, const Term< Coeff > &rhs)
	Perform a multiplication involving a term. More...
template<typename Coeff >
Term< Coeff >	operator* (Term< Coeff > lhs, const Monomial::Arg &rhs)
	Perform a multiplication involving a term. More...
template<typename Coeff >
Term< Coeff >	operator* (Term< Coeff > lhs, Variable rhs)
	Perform a multiplication involving a term. More...
template<typename Coeff >
Term< Coeff >	operator* (Term< Coeff > lhs, const Coeff &rhs)
	Perform a multiplication involving a term. More...
template<typename Coeff >
Term< Coeff >	operator* (const Monomial::Arg &lhs, const Term< Coeff > &rhs)
	Perform a multiplication involving a term. More...
template<typename Coeff , EnableIf< carl::is_number_type< Coeff >> = dummy>
Term< Coeff >	operator* (const Monomial::Arg &lhs, const Coeff &rhs)
	Perform a multiplication involving a term. More...
template<typename Coeff >
Term< Coeff >	operator* (Variable lhs, const Term< Coeff > &rhs)
	Perform a multiplication involving a term. More...
template<typename Coeff >
Term< Coeff >	operator* (Variable lhs, const Coeff &rhs)
	Perform a multiplication involving a term. More...
template<typename Coeff >
Term< Coeff >	operator* (const Coeff &lhs, const Term< Coeff > &rhs)
	Perform a multiplication involving a term. More...
template<typename Coeff , EnableIf< carl::is_number_type< Coeff >> = dummy>
Term< Coeff >	operator* (const Coeff &lhs, const Monomial::Arg &rhs)
	Perform a multiplication involving a term. More...
template<typename Coeff >
Term< Coeff >	operator* (const Coeff &lhs, Variable rhs)
	Perform a multiplication involving a term. More...
template<typename Coeff , EnableIf< carl::is_subset_of_rationals_type< Coeff >> = dummy>
Term< Coeff >	operator/ (const Term< Coeff > &lhs, const Coeff &rhs)
	Perform a multiplication involving a term. More...
template<typename Coeff , EnableIf< carl::is_subset_of_rationals_type< Coeff >> = dummy>
Term< Coeff >	operator/ (const Monomial::Arg &lhs, const Coeff &rhs)
	Perform a multiplication involving a term. More...
template<typename Coeff , EnableIf< carl::is_subset_of_rationals_type< Coeff >> = dummy>
Term< Coeff >	operator/ (Variable &lhs, const Coeff &rhs)
	Perform a multiplication involving a term. More...
template<typename P >
FactorizedPolynomial< P >	operator* (const FactorizedPolynomial< P > &_lhs, const FactorizedPolynomial< P > &_rhs)
	Perform a multiplication involving a polynomial. More...
template<typename P >
FactorizedPolynomial< P >	operator* (const FactorizedPolynomial< P > &_lhs, const typename FactorizedPolynomial< P >::CoeffType &_rhs)
	Perform a multiplication involving a polynomial. More...
template<typename P >
FactorizedPolynomial< P >	operator* (const typename FactorizedPolynomial< P >::CoeffType &_lhs, const FactorizedPolynomial< P > &_rhs)
	Perform a multiplication involving a polynomial. More...
template<typename P >
FactorizedPolynomial< P >	operator/ (const FactorizedPolynomial< P > &_lhs, const typename FactorizedPolynomial< P >::CoeffType &_rhs)
	Perform a multiplication involving a polynomial. More...
Comparison operators
bool	operator== (const Monomial &lhs, const Monomial &rhs)
	Compares two arguments where one is a Monomial and the other is either a monomial or a variable. More...
bool	operator== (const Monomial::Arg &lhs, const Monomial::Arg &rhs)
	Compares two arguments where one is a Monomial and the other is either a monomial or a variable. More...
bool	operator== (const Monomial::Arg &lhs, Variable rhs)
	Compares two arguments where one is a Monomial and the other is either a monomial or a variable. More...
bool	operator== (Variable lhs, const Monomial::Arg &rhs)
	Compares two arguments where one is a Monomial and the other is either a monomial or a variable. More...
bool	operator!= (const Monomial::Arg &lhs, const Monomial::Arg &rhs)
	Compares two arguments where one is a Monomial and the other is either a monomial or a variable. More...
bool	operator!= (const Monomial::Arg &lhs, Variable rhs)
	Compares two arguments where one is a Monomial and the other is either a monomial or a variable. More...
bool	operator!= (Variable lhs, const Monomial::Arg &rhs)
	Compares two arguments where one is a Monomial and the other is either a monomial or a variable. More...
bool	operator< (const Monomial::Arg &lhs, const Monomial::Arg &rhs)
	Compares two arguments where one is a Monomial and the other is either a monomial or a variable. More...
bool	operator< (const Monomial::Arg &lhs, Variable rhs)
	Compares two arguments where one is a Monomial and the other is either a monomial or a variable. More...
bool	operator< (Variable lhs, const Monomial::Arg &rhs)
	Compares two arguments where one is a Monomial and the other is either a monomial or a variable. More...
bool	operator<= (const Monomial::Arg &lhs, const Monomial::Arg &rhs)
	Compares two arguments where one is a Monomial and the other is either a monomial or a variable. More...
bool	operator<= (const Monomial::Arg &lhs, Variable rhs)
	Compares two arguments where one is a Monomial and the other is either a monomial or a variable. More...
bool	operator<= (Variable lhs, const Monomial::Arg &rhs)
	Compares two arguments where one is a Monomial and the other is either a monomial or a variable. More...
bool	operator> (const Monomial::Arg &lhs, const Monomial::Arg &rhs)
	Compares two arguments where one is a Monomial and the other is either a monomial or a variable. More...
bool	operator> (const Monomial::Arg &lhs, Variable rhs)
	Compares two arguments where one is a Monomial and the other is either a monomial or a variable. More...
bool	operator> (Variable lhs, const Monomial::Arg &rhs)
	Compares two arguments where one is a Monomial and the other is either a monomial or a variable. More...
bool	operator>= (const Monomial::Arg &lhs, const Monomial::Arg &rhs)
	Compares two arguments where one is a Monomial and the other is either a monomial or a variable. More...
bool	operator>= (const Monomial::Arg &lhs, Variable rhs)
	Compares two arguments where one is a Monomial and the other is either a monomial or a variable. More...
bool	operator>= (Variable lhs, const Monomial::Arg &rhs)
	Compares two arguments where one is a Monomial and the other is either a monomial or a variable. More...
template<typename Coeff >
bool	operator== (const Term< Coeff > &lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator== (const Term< Coeff > &lhs, const Monomial &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator== (const Term< Coeff > &lhs, Variable rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator== (const Term< Coeff > &lhs, const Coeff &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator== (const Monomial::Arg &lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator== (Variable lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator== (const Coeff &lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator!= (const Term< Coeff > &lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator!= (const Term< Coeff > &lhs, const Monomial::Arg &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator!= (const Term< Coeff > &lhs, Variable rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator!= (const Term< Coeff > &lhs, const Coeff &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator!= (const Monomial::Arg &lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator!= (Variable lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator!= (const Coeff &lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator< (const Term< Coeff > &lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator< (const Term< Coeff > &lhs, const Monomial::Arg &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator< (const Term< Coeff > &lhs, Variable rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator< (const Term< Coeff > &lhs, const Coeff &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator< (const Monomial::Arg &lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator< (Variable lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator< (const Coeff &lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator<= (const Term< Coeff > &lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator<= (const Term< Coeff > &lhs, const Monomial::Arg &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator<= (const Term< Coeff > &lhs, Variable rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator<= (const Term< Coeff > &lhs, const Coeff &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator<= (const Monomial::Arg &lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator<= (Variable lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator<= (const Coeff &lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator> (const Term< Coeff > &lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator> (const Term< Coeff > &lhs, const Monomial::Arg &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator> (const Term< Coeff > &lhs, Variable rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator> (const Term< Coeff > &lhs, const Coeff &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator> (const Monomial::Arg &lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator> (Variable lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator> (const Coeff &lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator>= (const Term< Coeff > &lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator>= (const Term< Coeff > &lhs, const Monomial::Arg &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator>= (const Term< Coeff > &lhs, Variable rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator>= (const Term< Coeff > &lhs, const Coeff &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator>= (const Monomial::Arg &lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator>= (Variable lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
template<typename Coeff >
bool	operator>= (const Coeff &lhs, const Term< Coeff > &rhs)
	Compares two arguments where one is a term and the other is either a term, a monomial or a variable. More...
Division operators
template<typename C , typename O , typename P , EnableIf< carl::is_number_type< C >> = dummy>
MultivariatePolynomial< C, O, P >	operator/ (const MultivariatePolynomial< C, O, P > &lhs, const C &rhs)
	Perform a division involving a polynomial. More...
Equality comparison operators
template<typename C , typename O , typename P >
bool	operator== (const MultivariatePolynomial< C, O, P > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the two arguments are equal. More...
template<typename C , typename O , typename P >
bool	operator== (const MultivariatePolynomial< C, O, P > &lhs, const Term< C > &rhs)
	Checks if the two arguments are equal. More...
template<typename C , typename O , typename P >
bool	operator== (const MultivariatePolynomial< C, O, P > &lhs, const Monomial::Arg &rhs)
	Checks if the two arguments are equal. More...
template<typename C , typename O , typename P >
bool	operator== (const MultivariatePolynomial< C, O, P > &lhs, Variable rhs)
	Checks if the two arguments are equal. More...
template<typename C , typename O , typename P >
bool	operator== (const MultivariatePolynomial< C, O, P > &lhs, const C &rhs)
	Checks if the two arguments are equal. More...
template<typename C , typename O , typename P , DisableIf< std::is_integral< C >> = dummy>
bool	operator== (const MultivariatePolynomial< C, O, P > &lhs, int rhs)
	Checks if the two arguments are equal. More...
template<typename C , typename O , typename P >
bool	operator== (const Term< C > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the two arguments are equal. More...
template<typename C , typename O , typename P >
bool	operator== (const Monomial::Arg &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the two arguments are equal. More...
template<typename C , typename O , typename P >
bool	operator== (Variable lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the two arguments are equal. More...
template<typename C , typename O , typename P >
bool	operator== (const C &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the two arguments are equal. More...
template<typename C , typename O , typename P >
bool	operator== (const UnivariatePolynomial< C > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the two arguments are equal. More...
template<typename C , typename O , typename P >
bool	operator== (const MultivariatePolynomial< C, O, P > &lhs, const UnivariatePolynomial< C > &rhs)
	Checks if the two arguments are equal. More...
template<typename C , typename O , typename P >
bool	operator== (const UnivariatePolynomial< MultivariatePolynomial< C >> &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the two arguments are equal. More...
template<typename C , typename O , typename P >
bool	operator== (const MultivariatePolynomial< C, O, P > &lhs, const UnivariatePolynomial< MultivariatePolynomial< C >> &rhs)
	Checks if the two arguments are equal. More...
template<typename P >
bool	operator== (const FactorizedPolynomial< P > &_lhs, const FactorizedPolynomial< P > &_rhs)
	Checks if the two arguments are equal. More...
template<typename P >
bool	operator== (const FactorizedPolynomial< P > &_lhs, const typename FactorizedPolynomial< P >::CoeffType &_rhs)
	Checks if the two arguments are equal. More...
template<typename P >
bool	operator== (const typename FactorizedPolynomial< P >::CoeffType &_lhs, const FactorizedPolynomial< P > &_rhs)
	Checks if the two arguments are equal. More...
Inequality comparison operators
template<typename C , typename O , typename P >
bool	operator!= (const MultivariatePolynomial< C, O, P > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the two arguments are not equal. More...
template<typename C , typename O , typename P >
bool	operator!= (const MultivariatePolynomial< C, O, P > &lhs, const Term< C > &rhs)
	Checks if the two arguments are not equal. More...
template<typename C , typename O , typename P >
bool	operator!= (const MultivariatePolynomial< C, O, P > &lhs, const Monomial::Arg &rhs)
	Checks if the two arguments are not equal. More...
template<typename C , typename O , typename P >
bool	operator!= (const MultivariatePolynomial< C, O, P > &lhs, Variable rhs)
	Checks if the two arguments are not equal. More...
template<typename C , typename O , typename P >
bool	operator!= (const MultivariatePolynomial< C, O, P > &lhs, const C &rhs)
	Checks if the two arguments are not equal. More...
template<typename C , typename O , typename P >
bool	operator!= (const Term< C > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the two arguments are not equal. More...
template<typename C , typename O , typename P >
bool	operator!= (const Monomial::Arg &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the two arguments are not equal. More...
template<typename C , typename O , typename P >
bool	operator!= (Variable lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the two arguments are not equal. More...
template<typename C , typename O , typename P >
bool	operator!= (const C &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the two arguments are not equal. More...
template<typename C , typename O , typename P >
bool	operator!= (const UnivariatePolynomial< C > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the two arguments are not equal. More...
template<typename C , typename O , typename P >
bool	operator!= (const MultivariatePolynomial< C, O, P > &lhs, const UnivariatePolynomial< C > &rhs)
	Checks if the two arguments are not equal. More...
template<typename C , typename O , typename P >
bool	operator!= (const UnivariatePolynomial< MultivariatePolynomial< C >> &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the two arguments are not equal. More...
template<typename C , typename O , typename P >
bool	operator!= (const MultivariatePolynomial< C, O, P > &lhs, const UnivariatePolynomial< MultivariatePolynomial< C >> &rhs)
	Checks if the two arguments are not equal. More...
template<typename P >
bool	operator!= (const FactorizedPolynomial< P > &_lhs, const FactorizedPolynomial< P > &_rhs)
	Checks if the two arguments are not equal. More...
template<typename P >
bool	operator!= (const FactorizedPolynomial< P > &_lhs, const typename FactorizedPolynomial< P >::CoeffType &_rhs)
	Checks if the two arguments are not equal. More...
template<typename P >
bool	operator!= (const typename FactorizedPolynomial< P >::CoeffType &_lhs, const FactorizedPolynomial< P > &_rhs)
	Checks if the two arguments are not equal. More...
Less than comparison operators
template<typename C , typename O , typename P >
bool	operator< (const MultivariatePolynomial< C, O, P > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first arguments is less than the second. More...
template<typename C , typename O , typename P >
bool	operator< (const MultivariatePolynomial< C, O, P > &lhs, const Term< C > &rhs)
	Checks if the first arguments is less than the second. More...
template<typename C , typename O , typename P >
bool	operator< (const MultivariatePolynomial< C, O, P > &lhs, const Monomial::Arg &rhs)
	Checks if the first arguments is less than the second. More...
template<typename C , typename O , typename P >
bool	operator< (const MultivariatePolynomial< C, O, P > &lhs, Variable rhs)
	Checks if the first arguments is less than the second. More...
template<typename C , typename O , typename P >
bool	operator< (const MultivariatePolynomial< C, O, P > &lhs, const C &rhs)
	Checks if the first arguments is less than the second. More...
template<typename C , typename O , typename P >
bool	operator< (const Term< C > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first arguments is less than the second. More...
template<typename C , typename O , typename P >
bool	operator< (const Monomial::Arg &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first arguments is less than the second. More...
template<typename C , typename O , typename P >
bool	operator< (Variable lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first arguments is less than the second. More...
template<typename C , typename O , typename P >
bool	operator< (const C &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first arguments is less than the second. More...
template<typename P >
bool	operator< (const FactorizedPolynomial< P > &_lhs, const FactorizedPolynomial< P > &_rhs)
	Checks if the first arguments is less than the second. More...
template<typename P >
bool	operator< (const FactorizedPolynomial< P > &_lhs, const typename FactorizedPolynomial< P >::CoeffType &_rhs)
	Checks if the first arguments is less than the second. More...
template<typename P >
bool	operator< (const typename FactorizedPolynomial< P >::CoeffType &_lhs, const FactorizedPolynomial< P > &_rhs)
	Checks if the first arguments is less than the second. More...
Greater than comparison operators
template<typename C , typename O , typename P >
bool	operator> (const MultivariatePolynomial< C, O, P > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first argument is greater than the second. More...
template<typename C , typename O , typename P >
bool	operator> (const MultivariatePolynomial< C, O, P > &lhs, const Term< C > &rhs)
	Checks if the first argument is greater than the second. More...
template<typename C , typename O , typename P >
bool	operator> (const MultivariatePolynomial< C, O, P > &lhs, const Monomial::Arg &rhs)
	Checks if the first argument is greater than the second. More...
template<typename C , typename O , typename P >
bool	operator> (const MultivariatePolynomial< C, O, P > &lhs, Variable rhs)
	Checks if the first argument is greater than the second. More...
template<typename C , typename O , typename P >
bool	operator> (const MultivariatePolynomial< C, O, P > &lhs, const C &rhs)
	Checks if the first argument is greater than the second. More...
template<typename C , typename O , typename P >
bool	operator> (const Term< C > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first argument is greater than the second. More...
template<typename C , typename O , typename P >
bool	operator> (const Monomial::Arg &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first argument is greater than the second. More...
template<typename C , typename O , typename P >
bool	operator> (Variable lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first argument is greater than the second. More...
template<typename C , typename O , typename P >
bool	operator> (const C &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first argument is greater than the second. More...
template<typename C , typename O , typename P >
bool	operator> (const UnivariatePolynomial< C > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first argument is greater than the second. More...
template<typename C , typename O , typename P >
bool	operator> (const MultivariatePolynomial< C, O, P > &lhs, const UnivariatePolynomial< C > &rhs)
	Checks if the first argument is greater than the second. More...
template<typename C , typename O , typename P >
bool	operator> (const UnivariatePolynomial< MultivariatePolynomial< C >> &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first argument is greater than the second. More...
template<typename C , typename O , typename P >
bool	operator> (const MultivariatePolynomial< C, O, P > &lhs, const UnivariatePolynomial< MultivariatePolynomial< C >> &rhs)
	Checks if the first argument is greater than the second. More...
template<typename P >
bool	operator> (const FactorizedPolynomial< P > &_lhs, const FactorizedPolynomial< P > &_rhs)
	Checks if the first arguments is greater than the second. More...
template<typename P >
bool	operator> (const FactorizedPolynomial< P > &_lhs, const typename FactorizedPolynomial< P >::CoeffType &_rhs)
	Checks if the first arguments is greater than the second. More...
template<typename P >
bool	operator> (const typename FactorizedPolynomial< P >::CoeffType &_lhs, const FactorizedPolynomial< P > &_rhs)
	Checks if the first arguments is greater than the second. More...
Less or equal comparison operators
template<typename C , typename O , typename P >
bool	operator<= (const MultivariatePolynomial< C, O, P > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first argument is less or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator<= (const MultivariatePolynomial< C, O, P > &lhs, const Term< C > &rhs)
	Checks if the first argument is less or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator<= (const MultivariatePolynomial< C, O, P > &lhs, const Monomial::Arg &rhs)
	Checks if the first argument is less or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator<= (const MultivariatePolynomial< C, O, P > &lhs, Variable rhs)
	Checks if the first argument is less or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator<= (const MultivariatePolynomial< C, O, P > &lhs, const C &rhs)
	Checks if the first argument is less or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator<= (const Term< C > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first argument is less or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator<= (const Monomial::Arg &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first argument is less or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator<= (Variable lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first argument is less or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator<= (const C &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first argument is less or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator<= (const UnivariatePolynomial< C > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first argument is less or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator<= (const MultivariatePolynomial< C, O, P > &lhs, const UnivariatePolynomial< C > &rhs)
	Checks if the first argument is less or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator<= (const UnivariatePolynomial< MultivariatePolynomial< C >> &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first argument is less or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator<= (const MultivariatePolynomial< C, O, P > &lhs, const UnivariatePolynomial< MultivariatePolynomial< C >> &rhs)
	Checks if the first argument is less or equal than the second. More...
template<typename P >
bool	operator<= (const FactorizedPolynomial< P > &_lhs, const FactorizedPolynomial< P > &_rhs)
	Checks if the first arguments is less or equal than the second. More...
template<typename P >
bool	operator<= (const FactorizedPolynomial< P > &_lhs, const typename FactorizedPolynomial< P >::CoeffType &_rhs)
	Checks if the first arguments is less or equal than the second. More...
template<typename P >
bool	operator<= (const typename FactorizedPolynomial< P >::CoeffType &_lhs, const FactorizedPolynomial< P > &_rhs)
	Checks if the first arguments is less or equal than the second. More...
Greater or equal comparison operators
template<typename C , typename O , typename P >
bool	operator>= (const MultivariatePolynomial< C, O, P > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first argument is greater or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator>= (const MultivariatePolynomial< C, O, P > &lhs, const Term< C > &rhs)
	Checks if the first argument is greater or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator>= (const MultivariatePolynomial< C, O, P > &lhs, const Monomial::Arg &rhs)
	Checks if the first argument is greater or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator>= (const MultivariatePolynomial< C, O, P > &lhs, Variable rhs)
	Checks if the first argument is greater or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator>= (const MultivariatePolynomial< C, O, P > &lhs, const C &rhs)
	Checks if the first argument is greater or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator>= (const Term< C > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first argument is greater or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator>= (const Monomial::Arg &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first argument is greater or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator>= (Variable lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first argument is greater or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator>= (const C &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first argument is greater or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator>= (const UnivariatePolynomial< C > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first argument is greater or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator>= (const MultivariatePolynomial< C, O, P > &lhs, const UnivariatePolynomial< C > &rhs)
	Checks if the first argument is greater or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator>= (const UnivariatePolynomial< MultivariatePolynomial< C >> &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Checks if the first argument is greater or equal than the second. More...
template<typename C , typename O , typename P >
bool	operator>= (const MultivariatePolynomial< C, O, P > &lhs, const UnivariatePolynomial< MultivariatePolynomial< C >> &rhs)
	Checks if the first argument is greater or equal than the second. More...
template<typename P >
bool	operator>= (const FactorizedPolynomial< P > &_lhs, const FactorizedPolynomial< P > &_rhs)
	Checks if the first arguments is greater or equal than the second. More...
template<typename P >
bool	operator>= (const FactorizedPolynomial< P > &_lhs, const typename FactorizedPolynomial< P >::CoeffType &_rhs)
	Checks if the first arguments is greater or equal than the second. More...
template<typename P >
bool	operator>= (const typename FactorizedPolynomial< P >::CoeffType &_lhs, const FactorizedPolynomial< P > &_rhs)
	Checks if the first arguments is greater or equal than the second. More...
Addition operators
template<typename C , typename O , typename P >
auto	operator+ (const MultivariatePolynomial< C, O, P > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Performs an addition involving a polynomial using operator+=(). More...
template<typename C , typename O , typename P >
auto	operator+ (const MultivariatePolynomial< C, O, P > &lhs, const Term< C > &rhs)
	Performs an addition involving a polynomial using operator+=(). More...
template<typename C , typename O , typename P >
auto	operator+ (const MultivariatePolynomial< C, O, P > &lhs, const Monomial::Arg &rhs)
	Performs an addition involving a polynomial using operator+=(). More...
template<typename C , typename O , typename P >
auto	operator+ (const MultivariatePolynomial< C, O, P > &lhs, Variable rhs)
	Performs an addition involving a polynomial using operator+=(). More...
template<typename C , typename O , typename P >
auto	operator+ (const MultivariatePolynomial< C, O, P > &lhs, const C &rhs)
	Performs an addition involving a polynomial using operator+=(). More...
template<typename C , typename O , typename P >
auto	operator+ (const Term< C > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Performs an addition involving a polynomial using operator+=(). More...
template<typename C >
auto	operator+ (const Term< C > &lhs, const Term< C > &rhs)
	Performs an addition involving a polynomial using operator+=(). More...
template<typename C >
auto	operator+ (const Term< C > &lhs, const Monomial::Arg &rhs)
	Performs an addition involving a polynomial using operator+=(). More...
template<typename C >
auto	operator+ (const Term< C > &lhs, Variable rhs)
	Performs an addition involving a polynomial using operator+=(). More...
template<typename C >
auto	operator+ (const Term< C > &lhs, const C &rhs)
	Performs an addition involving a polynomial using operator+=(). More...
template<typename C , typename O , typename P >
auto	operator+ (const Monomial::Arg &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Performs an addition involving a polynomial using operator+=(). More...
template<typename C >
auto	operator+ (const Monomial::Arg &lhs, const Term< C > &rhs)
	Performs an addition involving a polynomial using operator+=(). More...
template<typename C , EnableIf< carl::is_number_type< C >> = dummy>
auto	operator+ (const Monomial::Arg &lhs, const C &rhs)
	Performs an addition involving a polynomial using operator+=(). More...
template<typename C , typename O , typename P >
auto	operator+ (Variable lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Performs an addition involving a polynomial using operator+=(). More...
template<typename C >
auto	operator+ (Variable lhs, const Term< C > &rhs)
	Performs an addition involving a polynomial using operator+=(). More...
template<typename C , EnableIf< carl::is_number_type< C >> = dummy>
auto	operator+ (Variable lhs, const C &rhs)
	Performs an addition involving a polynomial using operator+=(). More...
template<typename C , typename O , typename P >
auto	operator+ (const C &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Performs an addition involving a polynomial using operator+=(). More...
template<typename C >
auto	operator+ (const C &lhs, const Term< C > &rhs)
	Performs an addition involving a polynomial using operator+=(). More...
template<typename C , EnableIf< carl::is_number_type< C >> = dummy>
auto	operator+ (const C &lhs, const Monomial::Arg &rhs)
	Performs an addition involving a polynomial using operator+=(). More...
template<typename C , EnableIf< carl::is_number_type< C >> = dummy>
auto	operator+ (const C &lhs, Variable rhs)
	Performs an addition involving a polynomial using operator+=(). More...
template<typename P >
FactorizedPolynomial< P >	operator+ (const FactorizedPolynomial< P > &_lhs, const FactorizedPolynomial< P > &_rhs)
	Performs an addition involving a polynomial. More...
template<typename P >
FactorizedPolynomial< P >	operator+ (const FactorizedPolynomial< P > &_lhs, const typename FactorizedPolynomial< P >::CoeffType &_rhs)
	Performs an addition involving a polynomial. More...
template<typename P >
FactorizedPolynomial< P >	operator+ (const typename FactorizedPolynomial< P >::CoeffType &_lhs, const FactorizedPolynomial< P > &_rhs)
	Performs an addition involving a polynomial. More...
Subtraction operators
template<typename C , typename O , typename P >
auto	operator- (const MultivariatePolynomial< C, O, P > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Performs a subtraction involving a polynomial using operator-=(). More...
template<typename C , typename O , typename P >
auto	operator- (const MultivariatePolynomial< C, O, P > &lhs, const Term< C > &rhs)
	Performs a subtraction involving a polynomial using operator-=(). More...
template<typename C , typename O , typename P >
auto	operator- (const MultivariatePolynomial< C, O, P > &lhs, const Monomial::Arg &rhs)
	Performs a subtraction involving a polynomial using operator-=(). More...
template<typename C , typename O , typename P >
auto	operator- (const MultivariatePolynomial< C, O, P > &lhs, Variable rhs)
	Performs a subtraction involving a polynomial using operator-=(). More...
template<typename C , typename O , typename P >
auto	operator- (const MultivariatePolynomial< C, O, P > &lhs, const C &rhs)
	Performs a subtraction involving a polynomial using operator-=(). More...
template<typename C , typename O , typename P >
auto	operator- (const Term< C > &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Performs a subtraction involving a polynomial using operator-=(). More...
template<typename C >
auto	operator- (const Term< C > &lhs, const Term< C > &rhs)
	Performs a subtraction involving a polynomial using operator-=(). More...
template<typename C >
auto	operator- (const Term< C > &lhs, const Monomial::Arg &rhs)
	Performs a subtraction involving a polynomial using operator-=(). More...
template<typename C >
auto	operator- (const Term< C > &lhs, Variable rhs)
	Performs a subtraction involving a polynomial using operator-=(). More...
template<typename C >
auto	operator- (const Term< C > &lhs, const C &rhs)
	Performs a subtraction involving a polynomial using operator-=(). More...
template<typename C , typename O , typename P >
auto	operator- (const Monomial::Arg &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Performs a subtraction involving a polynomial using operator-=(). More...
template<typename C >
auto	operator- (const Monomial::Arg &lhs, const Term< C > &rhs)
	Performs a subtraction involving a polynomial using operator-=(). More...
template<typename C , EnableIf< carl::is_number_type< C >> = dummy>
auto	operator- (const Monomial::Arg &lhs, const C &rhs)
	Performs a subtraction involving a polynomial using operator-=(). More...
template<typename C , typename O , typename P >
auto	operator- (Variable lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Performs a subtraction involving a polynomial using operator-=(). More...
template<typename C >
auto	operator- (Variable lhs, const Term< C > &rhs)
	Performs a subtraction involving a polynomial using operator-=(). More...
template<typename C , EnableIf< carl::is_number_type< C >> = dummy>
auto	operator- (Variable lhs, const C &rhs)
	Performs a subtraction involving a polynomial using operator-=(). More...
template<typename C , typename O , typename P >
auto	operator- (const C &lhs, const MultivariatePolynomial< C, O, P > &rhs)
	Performs a subtraction involving a polynomial using operator-=(). More...
template<typename C >
auto	operator- (const C &lhs, const Term< C > &rhs)
	Performs a subtraction involving a polynomial using operator-=(). More...
template<typename C , EnableIf< carl::is_number_type< C >> = dummy>
auto	operator- (const C &lhs, const Monomial::Arg &rhs)
	Performs a subtraction involving a polynomial using operator-=(). More...
template<typename C , EnableIf< carl::is_number_type< C >> = dummy>
auto	operator- (const C &lhs, Variable rhs)
	Performs a subtraction involving a polynomial using operator-=(). More...
template<typename P >
FactorizedPolynomial< P >	operator- (const FactorizedPolynomial< P > &_lhs, const FactorizedPolynomial< P > &_rhs)
	Performs an subtraction involving a polynomial. More...
template<typename P >
FactorizedPolynomial< P >	operator- (const FactorizedPolynomial< P > &_lhs, const typename FactorizedPolynomial< P >::CoeffType &_rhs)
	Performs an subtraction involving a polynomial. More...
template<typename P >
FactorizedPolynomial< P >	operator- (const typename FactorizedPolynomial< P >::CoeffType &_lhs, const FactorizedPolynomial< P > &_rhs)
	Performs an subtraction involving a polynomial. More...
In-place multiplication operators
template<typename Coeff >
Term< Coeff > &	operator*= (Term< Coeff > &lhs, const Coeff &rhs)
	Multiply a term with something and return the changed term. More...
template<typename Coeff >
Term< Coeff > &	operator*= (Term< Coeff > &lhs, Variable rhs)
	Multiply a term with something and return the changed term. More...
template<typename Coeff >
Term< Coeff > &	operator*= (Term< Coeff > &lhs, const Monomial::Arg &rhs)
	Multiply a term with something and return the changed term. More...
template<typename Coeff >
Term< Coeff > &	operator*= (Term< Coeff > &lhs, const Term< Coeff > &rhs)
	Multiply a term with something and return the changed term. More...

Variables
const signed	A_IFF_B = 2
const signed	A_IMPLIES_B = 1
const signed	B_IMPLIES_A = -1
const signed	NOT__A_AND_B = -2
const signed	A_AND_B__IFF_C = -3
const signed	A_XOR_B = -4
static int	initvariable = initialize()
	Call to initialize. More...
static const cln::cl_RA	ONE_DIVIDED_BY_10_TO_THE_POWER_OF_23 = cln::cl_RA(1)/cln::expt(cln::cl_RA(10), 23)
static const cln::cl_RA	ONE_DIVIDED_BY_10_TO_THE_POWER_OF_52 = cln::cl_RA(1)/cln::expt(cln::cl_RA(10), 52)
static std::map< Variable, Interval< double > >	mMap = {{ Variable::NO_VARIABLE , Interval<double>(0)}}
constexpr unsigned	sizeOfUnsigned = sizeof(unsigned)
std::string	last_assertion_string
	Stores a textual representation of the last assertion that was registered via REGISTER_ASSERT. More...
int	last_assertion_code = 23
	Stores an integer representation of the last assertion that was registered via REGISTER_ASSERT. More...
static bool	signal_installed = install_signal_handler()
	Static variable that ensures that install_signal_handler is called. More...
const dtl::enabled	dummy = {}
template<class >
constexpr bool	dependent_false_v = false
static constexpr std::size_t	CONDITION_SIZE = 64
static constexpr Condition	PROP_TRUE = Condition()
static constexpr Condition	PROP_IS_IN_NNF = Condition( 0 )
static constexpr Condition	PROP_IS_IN_CNF = Condition( 1 )
static constexpr Condition	PROP_IS_PURE_CONJUNCTION = Condition( 2 )
static constexpr Condition	PROP_IS_A_CLAUSE = Condition( 3 )
static constexpr Condition	PROP_IS_A_LITERAL = Condition( 4 )
static constexpr Condition	PROP_IS_AN_ATOM = Condition( 5 )
static constexpr Condition	PROP_IS_LITERAL_CONJUNCTION = Condition( 6 )
static constexpr Condition	PROP_IS_IN_PNF = Condition( 7 )
static const Condition	STRONG_CONDITIONS
static constexpr Condition	PROP_CONTAINS_EQUATION = Condition( 16 )
static constexpr Condition	PROP_CONTAINS_INEQUALITY = Condition( 17 )
static constexpr Condition	PROP_CONTAINS_STRICT_INEQUALITY = Condition( 18 )
static constexpr Condition	PROP_CONTAINS_LINEAR_POLYNOMIAL = Condition( 19 )
static constexpr Condition	PROP_CONTAINS_NONLINEAR_POLYNOMIAL = Condition( 20 )
static constexpr Condition	PROP_CONTAINS_MULTIVARIATE_POLYNOMIAL = Condition( 21 )
static constexpr Condition	PROP_CONTAINS_BOOLEAN = Condition( 22 )
static constexpr Condition	PROP_CONTAINS_INTEGER_VALUED_VARS = Condition( 23 )
static constexpr Condition	PROP_CONTAINS_REAL_VALUED_VARS = Condition( 24 )
static constexpr Condition	PROP_CONTAINS_UNINTERPRETED_EQUATIONS = Condition( 25 )
static constexpr Condition	PROP_CONTAINS_BITVECTOR = Condition( 26 )
static constexpr Condition	PROP_CONTAINS_PSEUDOBOOLEAN = Condition( 27 )
static constexpr Condition	PROP_VARIABLE_DEGREE_GREATER_THAN_TWO = Condition( 28 )
static constexpr Condition	PROP_VARIABLE_DEGREE_GREATER_THAN_THREE = Condition( 29 )
static constexpr Condition	PROP_VARIABLE_DEGREE_GREATER_THAN_FOUR = Condition( 30 )
static constexpr Condition	PROP_CONTAINS_WEAK_INEQUALITY = Condition( 31 )
static constexpr Condition	PROP_CONTAINS_QUANTIFIER_EXISTS = Condition( 32 )
static constexpr Condition	PROP_CONTAINS_QUANTIFIER_FORALL = Condition( 33 )
static const Condition	WEAK_CONDITIONS

Detailed Description

carl is the main namespace for the library.

This file provides mechanisms to substitute a model into an expression and to evaluate an expression over a model.

Condition.h.

Class to create a square root expression object.

Everything included in this library is found in this namespace.

Author

Florian Corzilius

Since

2011-05-26

Version

2013-10-22

Author

Florian Corziliuscorzi.nosp@m.lius.nosp@m.@cs.r.nosp@m.wth-.nosp@m.aache.nosp@m.n.de

Since

2012-06-11

Version

2014-10-30

Typedef Documentation

Assignment

template<typename T >

using carl::Assignment = typedef std::map<Variable, T>

Definition at line 13 of file Common.h.

Bool

template<bool B, typename... T>

using carl::Bool = typedef typename dependent_bool_type<B, T...>::type

Definition at line 27 of file SFINAE.h.

Coeff

template<typename P >

using carl::Coeff = typedef typename UnderlyingNumberType<P>::type

Definition at line 20 of file FactorizedPolynomial.h.

CoeffMatrix

template<typename Coeff >

using carl::CoeffMatrix = typedef Eigen::Matrix<Coeff, Eigen::Dynamic, Eigen::Dynamic>

Definition at line 37 of file CharPol.h.

Conditional

template<bool If, typename Then , typename Else >

using carl::Conditional = typedef typename std::conditional<If, Then, Else>::type

Definition at line 22 of file SFINAE.h.

ConstraintBounds

template<typename Pol >

using carl::ConstraintBounds = typedef FastMap<Pol, std::map<typename Pol::NumberType, std::pair<Relation,Formula<Pol> >> >

A map from formula pointers to a map of rationals to a pair of a constraint relation and a formula pointer. (internally used)

Definition at line 7 of file ConstraintBounds.h.

ConstraintPool

template<typename Pol >

using carl::ConstraintPool = typedef pool::Pool<CachedConstraintContent<Pol> >

Definition at line 54 of file Constraint.h.

Constraints

template<typename Poly >

using carl::Constraints = typedef std::set<Constraint<Poly>, carl::less<Constraint<Poly>, false> >

Definition at line 28 of file Constraint.h.

CritPairs

typedef CriticalPairs<Heap, CriticalPairConfiguration<GrLexOrdering> > carl::CritPairs

Definition at line 115 of file CriticalPairs.h.

DisableIf

template<typename... Condition>

using carl::DisableIf = typedef typename std::enable_if<Not<any<Condition...> >::value, dtl::enabled>::type

Definition at line 66 of file SFINAE.h.

EnableIf

template<typename... Condition>

using carl::EnableIf = typedef typename std::enable_if<all<Condition...>::value, dtl::enabled>::type

Definition at line 64 of file SFINAE.h.

EnableIfBool

template<bool Condition>

using carl::EnableIfBool = typedef typename std::enable_if<Condition, dtl::enabled>::type

Definition at line 68 of file SFINAE.h.

EncodingCache

template<typename Poly >

using carl::EncodingCache = typedef std::map<MultivariateRoot<Poly>, std::pair<std::vector<BasicConstraint<Poly> >, Variable> >

Definition at line 45 of file Encoding.h.

exponent

using carl::exponent = typedef std::size_t

Type of an exponent.

Definition at line 29 of file Monomial.h.

FactorMap

template<typename Coefficient >

using carl::FactorMap = typedef std::map<UnivariatePolynomial<Coefficient>, uint>

Definition at line 35 of file UnivariatePolynomial.h.

Factors

template<typename Pol >

using carl::Factors = typedef std::map<Pol,uint>

Definition at line 21 of file Common.h.

FastMap

template<typename T1 , typename T2 >

using carl::FastMap = typedef std::unordered_map<T1, T2, std::hash<T1> >

Definition at line 67 of file container_types.h.

FastPointerMap

template<typename T1 , typename T2 >

using carl::FastPointerMap = typedef std::unordered_map<const T1*, T2, pointerHash<T1>, pointerEqual<T1> >

Definition at line 73 of file container_types.h.

FastPointerMapB

template<typename T1 , typename T2 >

using carl::FastPointerMapB = typedef std::unordered_map<const T1*, T2, pointerHashWithNull<T1>, pointerEqualWithNull<T1> >

Definition at line 85 of file container_types.h.

FastPointerSet

template<typename T >

using carl::FastPointerSet = typedef std::unordered_set<const T*, pointerHash<T>, pointerEqual<T> >

Definition at line 70 of file container_types.h.

FastPointerSetB

template<typename T >

using carl::FastPointerSetB = typedef std::unordered_set<const T*, pointerHashWithNull<T>, pointerEqualWithNull<T> >

Definition at line 82 of file container_types.h.

FastSet

template<typename T >

using carl::FastSet = typedef std::unordered_set<T, std::hash<T> >

Definition at line 64 of file container_types.h.

FastSharedPointerMap

template<typename T1 , typename T2 >

using carl::FastSharedPointerMap = typedef std::unordered_map<std::shared_ptr<const T1>, T2, sharedPointerHash<T1>, sharedPointerEqual<T1> >

Definition at line 79 of file container_types.h.

FastSharedPointerMapB

template<typename T1 , typename T2 >

using carl::FastSharedPointerMapB = typedef std::unordered_map<std::shared_ptr<const T1>, T2, sharedPointerHashWithNull<T1>, pointerEqualWithNull<T1> >

Definition at line 91 of file container_types.h.

FastSharedPointerSet

template<typename T >

using carl::FastSharedPointerSet = typedef std::unordered_set<std::shared_ptr<const T>, sharedPointerHash<T>, sharedPointerEqual<T> >

Definition at line 76 of file container_types.h.

FastSharedPointerSetB

template<typename T >

using carl::FastSharedPointerSetB = typedef std::unordered_set<std::shared_ptr<const T>, sharedPointerHashWithNull<T>, pointerEqualWithNull<T> >

Definition at line 88 of file container_types.h.

Formulas

template<typename Poly >

using carl::Formulas = typedef std::vector<Formula<Poly> >

Definition at line 18 of file FormulaContent.h.

FormulaSet

template<typename Poly >

using carl::FormulaSet = typedef std::set<Formula<Poly> >

Definition at line 20 of file FormulaContent.h.

FormulasMulti

template<typename Poly >

using carl::FormulasMulti = typedef std::multiset<Formula<Poly> >

Definition at line 22 of file FormulaContent.h.

GrLexOrdering

using carl::GrLexOrdering = typedef MonomialComparator<Monomial::compareGradedLexical, true >

Definition at line 63 of file MonomialOrdering.h.

IntegralTypeIfDifferent

template<typename C >

using carl::IntegralTypeIfDifferent = typedef typename std::enable_if<!std::is_same<C, typename IntegralType<C>::type>::value, typename IntegralType<C>::type>::type

Definition at line 321 of file typetraits.h.

LexOrdering

using carl::LexOrdering = typedef MonomialComparator<Monomial::compareLexical, false >

Definition at line 62 of file MonomialOrdering.h.

ModelSubstitutionPtr

template<typename Rational , typename Poly >

using carl::ModelSubstitutionPtr = typedef std::unique_ptr<ModelSubstitution<Rational,Poly> >

Definition at line 24 of file ModelValue.h.

MonomialOrderingFunction

using carl::MonomialOrderingFunction = typedef CompareResult(*)(const Monomial::Arg&, const Monomial::Arg&)

Definition at line 14 of file MonomialOrdering.h.

Not

template<typename T >

using carl::Not = typedef Bool<!T::value>

Meta-logical negation.

Definition at line 31 of file SFINAE.h.

OrderedAssignment

template<typename T >

using carl::OrderedAssignment = typedef std::vector<std::pair<Variable, T> >

Definition at line 16 of file Common.h.

pointerEqual

template<typename T >

using carl::pointerEqual = typedef carl::equal_to<const T*, false>

Definition at line 18 of file container_types.h.

pointerEqualWithNull

template<typename T >

using carl::pointerEqualWithNull = typedef carl::equal_to<const T*, true>

Definition at line 20 of file container_types.h.

pointerHash

template<typename T >

using carl::pointerHash = typedef carl::hash<T*, false>

Definition at line 36 of file container_types.h.

pointerHashWithNull

template<typename T >

using carl::pointerHashWithNull = typedef carl::hash<T*, true>

Definition at line 38 of file container_types.h.

pointerLess

template<typename T >

using carl::pointerLess = typedef carl::less<const T*, false>

Definition at line 27 of file container_types.h.

pointerLessWithNull

template<typename T >

using carl::pointerLessWithNull = typedef carl::less<const T*, true>

Definition at line 29 of file container_types.h.

PointerMap

template<typename T1 , typename T2 >

using carl::PointerMap = typedef std::map<const T1*, T2, pointerLess<T1> >

Definition at line 52 of file container_types.h.

PointerMultiSet

template<typename T >

using carl::PointerMultiSet = typedef std::multiset<const T*, pointerLess<T> >

Definition at line 49 of file container_types.h.

PointerSet

template<typename T >

using carl::PointerSet = typedef std::set<const T*, pointerLess<T> >

Definition at line 46 of file container_types.h.

precision_t

using carl::precision_t = typedef std::size_t

Definition at line 30 of file FLOAT_T.h.

QuantifierPrefix

using carl::QuantifierPrefix = typedef std::vector<std::pair<Quantifier, carl::Variable> >

Definition at line 28 of file PNF.h.

sharedPointerEqual

template<typename T >

using carl::sharedPointerEqual = typedef carl::equal_to<std::shared_ptr<const T>, false>

Definition at line 22 of file container_types.h.

sharedPointerEqualWithNull

template<typename T >

using carl::sharedPointerEqualWithNull = typedef carl::equal_to<std::shared_ptr<const T>, true>

Definition at line 24 of file container_types.h.

sharedPointerHash

template<typename T >

using carl::sharedPointerHash = typedef carl::hash<std::shared_ptr<const T>*, false>

Definition at line 40 of file container_types.h.

sharedPointerHashWithNull

template<typename T >

using carl::sharedPointerHashWithNull = typedef carl::hash<std::shared_ptr<const T>*, true>

Definition at line 42 of file container_types.h.

sharedPointerLess

template<typename T >

using carl::sharedPointerLess = typedef carl::less<std::shared_ptr<const T>*, false>

Definition at line 31 of file container_types.h.

sharedPointerLessWithNull

template<typename T >

using carl::sharedPointerLessWithNull = typedef carl::less<std::shared_ptr<const T>, true>

Definition at line 33 of file container_types.h.

SharedPointerMap

template<typename T1 , typename T2 >

using carl::SharedPointerMap = typedef std::map<std::shared_ptr<const T1>, T2, sharedPointerLess<T1> >

Definition at line 61 of file container_types.h.

SharedPointerMultiSet

template<typename T >

using carl::SharedPointerMultiSet = typedef std::multiset<std::shared_ptr<const T>, sharedPointerLess<T> >

Definition at line 58 of file container_types.h.

SharedPointerSet

template<typename T >

using carl::SharedPointerSet = typedef std::set<std::shared_ptr<const T>, sharedPointerLess<T> >

Definition at line 55 of file container_types.h.

sint

using carl::sint = typedef std::int64_t

Definition at line 17 of file numbers.h.

TypeInfoPair

template<typename T , class I >

using carl::TypeInfoPair = typedef std::pair<T*,I>

Definition at line 21 of file Cache.h.

uint

using carl::uint = typedef std::uint64_t

Definition at line 16 of file numbers.h.

UnivariatePolynomialPtr

template<typename Coefficient >

using carl::UnivariatePolynomialPtr = typedef std::shared_ptr<UnivariatePolynomial<Coefficient> >

Definition at line 32 of file UnivariatePolynomial.h.

Variables

using carl::Variables = typedef std::set<Variable>

Definition at line 18 of file Common.h.

Enumeration Type Documentation

BoundType

enum carl::BoundType

strong

Enumerator
STRICT	the given bound is compared by a strict ordering relation
WEAK	the given bound is compared by a weak ordering relation
INFTY	the given bound is interpreted as minus or plus infinity depending on whether it is the left or the right bound

Definition at line 13 of file BoundType.h.

BVCompareRelation

enum carl::BVCompareRelation : unsigned

strong

Enumerator
EQ
NEQ
ULT
ULE
UGT
UGE
SLT
SLE
SGT
SGE

Definition at line 15 of file BVCompareRelation.h.

BVTermType

enum carl::BVTermType

strong

Enumerator
CONSTANT
VARIABLE
CONCAT
EXTRACT
NOT
NEG
AND
OR
XOR
NAND
NOR
XNOR
ADD
SUB
MUL
DIV_U
DIV_S
MOD_U
MOD_S1
MOD_S2
EQ
LSHIFT
RSHIFT_LOGIC
RSHIFT_ARITH
LROTATE
RROTATE
EXT_U
EXT_S
REPEAT

Definition at line 10 of file BVTermType.h.

CARL_RND

enum carl::CARL_RND : int

strong

Enumerator
N
Z
U
D
A

Definition at line 23 of file roundingConversion.h.

CompareResult

enum carl::CompareResult

strong

Enumerator
LESS
EQUAL
GREATER

Definition at line 12 of file CompareResult.h.

Definiteness

enum carl::Definiteness

strong

Regarding a polynomial as a function , its definiteness gives information about the codomain .

Enumerator
NEGATIVE	Indicates that .
NEGATIVE_SEMI	Indicates that .
NON	Indicates that values may be positive and negative.
POSITIVE_SEMI	Indicates that .
POSITIVE	Indicates that .

Definition at line 16 of file Definiteness.h.

FormulaType

enum carl::FormulaType

Represent the type of a formula to allow faster/specialized processing.

For each (supported) SMTLIB theory, we have

• Constants
• Variables
• Functions
• Additional functions (not specified, but used in the wild)

Enumerator
ITE
EXISTS
FORALL
TRUE
FALSE
BOOL
NOT
NOT
IMPLIES
AND
AND
OR
OR
XOR
XOR
IFF
CONSTRAINT
VARCOMPARE
VARASSIGN
BITVECTOR
UEQ

Definition at line 35 of file FormulaContent.h.

Logic

enum carl::Logic

strong

Enumerator
QF_BV
QF_IDL
QF_LIA
QF_LIRA
QF_LRA
QF_NIA
QF_NIRA
QF_NRA
QF_PB
QF_RDL
QF_UF
NRA
LRA
UNDEFINED

Definition at line 7 of file Logic.h.

PolynomialComparisonOrder

enum carl::PolynomialComparisonOrder

strong

Enumerator
CauchyBound
LowDegree
Memory
Default

Definition at line 46 of file UnivariatePolynomial.h.

Quantifier

enum carl::Quantifier

strong

Enumerator
EXISTS
FORALL
FREE

Definition at line 9 of file PNF.h.

Relation

enum carl::Relation

strong

Enumerator
EQ
NEQ
LESS
LEQ
GREATER
GEQ

Definition at line 20 of file Relation.h.

Sign

enum carl::Sign

strong

This class represents the sign of a number .

Enumerator
NEGATIVE	Indicates that .
ZERO	Indicates that .
POSITIVE	Indicates that .

Definition at line 20 of file Sign.h.

Str2Double_Error

enum carl::Str2Double_Error

Enumerator
FLOAT_SUCCESS
FLOAT_OVERFLOW
FLOAT_UNDERFLOW
FLOAT_INCONVERTIBLE

Definition at line 60 of file FLOAT_T.h.

SubresultantStrategy

enum carl::SubresultantStrategy

strong

Enumerator
Generic
Lazard
Ducos
Default

Definition at line 16 of file Resultant.h.

ThomComparisonResult

enum carl::ThomComparisonResult

Enumerator
LESS
LESS
LESS
EQUAL
EQUAL
GREATER
GREATER
GREATER

Definition at line 15 of file SignCondition.h.

variableSelectionHeurisics

enum carl::variableSelectionHeurisics

Enumerator
GREEDY_I
GREEDY_Is
GREEDY_II
GREEDY_IIs

Definition at line 3 of file MultivariateHornerSettings.h.

VariableType

enum carl::VariableType

strong

Several types of variables are supported.

BOOL: the Booleans REAL: the reals INT: the integers UNINTERPRETED: all uninterpreted types BITVECTOR: bitvectors of any length

Enumerator
VT_BOOL
VT_REAL
VT_INT
VT_UNINTERPRETED
VT_BITVECTOR
MIN_TYPE
MAX_TYPE
TYPE_SIZE

Definition at line 28 of file Variable.h.

Function Documentation

abs() [1/10]

cln::cl_I carl::abs ( const cln::cl_I &  n )

inline

Get absolute value of an integer.

Parameters

n	An integer.

Returns

.

Definition at line 237 of file operations.h.

Here is the call graph for this function:

abs() [2/10]

cln::cl_RA carl::abs ( const cln::cl_RA &  n )

inline

Get absolute value of a fraction.

Parameters

n	A fraction.

Returns

.

Definition at line 246 of file operations.h.

Here is the call graph for this function:

abs() [3/10]

template<typename FloatType >

FLOAT_T<FloatType> carl::abs ( const FLOAT_T< FloatType > &  _in )

inline

Method which returns the absolute value of the passed number.

Parameters

_in

Number.

Returns

Number which holds the result.

Definition at line 1412 of file FLOAT_T.h.

Here is the call graph for this function:

Here is the caller graph for this function:

abs() [4/10]

template<typename IntegerT >

GFNumber<IntegerT> carl::abs

(

const GFNumber< IntegerT > &

n

)

Definition at line 190 of file GFNumber.h.

abs() [5/10]

template<typename Number >

Interval<Number> carl::abs ( const Interval< Number > &  _in )

inline

Method which returns the absolute value of the passed number.

Parameters

_in

Number.

Returns

Number which holds the result.

Definition at line 1511 of file Interval.h.

Here is the call graph for this function:

Here is the caller graph for this function:

abs() [6/10]

template<typename Number >

static IntRepRealAlgebraicNumber<Number> carl::abs ( const IntRepRealAlgebraicNumber< Number > &  n )

static

Definition at line 317 of file Ran.h.

Here is the call graph for this function:

abs() [7/10]

mpq_class carl::abs ( const mpq_class &  n )

inline

Definition at line 258 of file operations.h.

abs() [8/10]

mpz_class carl::abs ( const mpz_class &  n )

inline

Basic Operators.

The following functions implement simple operations on the given numbers.

Definition at line 252 of file operations.h.

abs() [9/10]

template<typename Number >

RealAlgebraicNumberThom<Number> carl::abs

(

const RealAlgebraicNumberThom< Number > &

n

)

Definition at line 143 of file ran_thom.h.

abs() [10/10]

double carl::abs ( double  n )

inline

Definition at line 127 of file operations.h.

Here is the caller graph for this function:

acos() [1/3]

template<typename FloatType >

FLOAT_T<FloatType> carl::acos ( const FLOAT_T< FloatType > &  _in )

inline

Definition at line 1484 of file FLOAT_T.h.

Here is the call graph for this function:

Here is the caller graph for this function:

acos() [2/3]

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

Interval<Number> carl::acos

(

const Interval< Number > &

i

)

Definition at line 58 of file Trigonometry.h.

Here is the call graph for this function:

Here is the caller graph for this function:

acos() [3/3]

double carl::acos ( double  in )

inline

Definition at line 161 of file operations.h.

acos_assign()

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

void carl::acos_assign

(

Interval< Number > &

i

)

Definition at line 64 of file Trigonometry.h.

Here is the call graph for this function:

acosh()

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

Interval<Number> carl::acosh

(

const Interval< Number > &

i

)

Definition at line 130 of file Trigonometry.h.

Here is the call graph for this function:

Here is the caller graph for this function:

acosh_assign()

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

void carl::acosh_assign

(

Interval< Number > &

i

)

Definition at line 136 of file Trigonometry.h.

Here is the call graph for this function:

addConstraintBound()

template<typename Pol >

Formula<Pol> carl::addConstraintBound	(	ConstraintBounds< Pol > &	_constraintBounds,
		const Formula< Pol > &	_constraint,
		bool	_inConjunction
	)

Adds the bound to the bounds of the polynomial specified by this constraint.

E.g., if the constraint is p+b~0, where p is a sum of terms, being a rational (actually integer) coefficient times a non-trivial (!=1) monomial( product of variables to the power of an exponent), b is a rational and ~ is any constraint relation. Furthermore, the leading coefficient of p is 1. Then we add the bound -b to the bounds of p (means that p ~ -b) stored in the given constraint bounds.

Parameters

_constraintBounds	An object collecting bounds of polynomials.
_constraint	The constraint to find a bound for a polynomial for.
_inConjunction	true, if the constraint is part of a conjunction. false, if the constraint is part of a disjunction.

Returns

Formula<Pol>( FALSE ), if the yet determined bounds imply that the conjunction (_inConjunction == true) or disjunction (_inConjunction == false) of which we got the given constraint is invalid resp. valid; false, the added constraint.

Definition at line 25 of file ConstraintBounds.h.

Here is the call graph for this function:

Here is the caller graph for this function:

AlmostEqual2sComplement()

template<typename Number >

bool carl::AlmostEqual2sComplement ( const Number &  A, const Number &  B, unsigned  = 128  )

inline

Definition at line 83 of file FLOAT_T.h.

Here is the caller graph for this function:

AlmostEqual2sComplement< double >()

template<>

bool carl::AlmostEqual2sComplement< double > ( const double &  A, const double &  B, unsigned  maxUlps  )

inline

Definition at line 89 of file FLOAT_T.h.

Here is the call graph for this function:

Here is the caller graph for this function:

AlmostEqual2sComplement< FLOAT_T< double > >()

template<>

bool carl::AlmostEqual2sComplement< FLOAT_T< double > > ( const FLOAT_T< double > &  A, const FLOAT_T< double > &  B, unsigned  maxUlps  )

inline

Definition at line 1609 of file FLOAT_T.h.

Here is the call graph for this function:

arithmetic_constraints() [1/2]

template<typename Pol >

void carl::arithmetic_constraints	(	const Formula< Pol > &	f,
		std::vector< Constraint< Pol >> &	constraints
	)

Collects all constraint occurring in this formula.

Parameters

constraints

The container to insert the constraint into.

Definition at line 79 of file Variables.h.

Here is the call graph for this function:

arithmetic_constraints() [2/2]

template<typename Pol >

void carl::arithmetic_constraints	(	const Formula< Pol > &	f,
		std::vector< Formula< Pol >> &	constraints
	)

Collects all constraint occurring in this formula.

Parameters

constraints

The container to insert the constraint into.

Definition at line 97 of file Variables.h.

Here is the call graph for this function:

arithmetic_variables()

template<typename T >

carlVariables carl::arithmetic_variables ( const T &  t )

inline

Definition at line 247 of file Variables.h.

Here is the call graph for this function:

as_constraint()

template<typename Poly , std::enable_if_t<!needs_context_type< Poly >::value, bool > = true>

std::optional< BasicConstraint< Poly > > carl::as_constraint

(

const VariableComparison< Poly > &

f

)

Convert this variable comparison "v < root(..)" into a simpler polynomial (in)equality against zero "p(..) < 0" if that is possible.

Returns

std::nullopt if conversion impossible.

Definition at line 98 of file VariableComparison.h.

Here is the call graph for this function:

Here is the caller graph for this function:

asin() [1/2]

template<typename FloatType >

FLOAT_T<FloatType> carl::asin ( const FLOAT_T< FloatType > &  _in )

inline

Definition at line 1476 of file FLOAT_T.h.

Here is the call graph for this function:

Here is the caller graph for this function:

asin() [2/2]

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

Interval<Number> carl::asin

(

const Interval< Number > &

i

)

Definition at line 46 of file Trigonometry.h.

Here is the call graph for this function:

Here is the caller graph for this function:

asin_assign()

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

void carl::asin_assign

(

Interval< Number > &

i

)

Definition at line 52 of file Trigonometry.h.

Here is the call graph for this function:

asinh()

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

Interval<Number> carl::asinh

(

const Interval< Number > &

i

)

Definition at line 118 of file Trigonometry.h.

Here is the call graph for this function:

Here is the caller graph for this function:

asinh_assign()

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

void carl::asinh_assign

(

Interval< Number > &

i

)

Definition at line 124 of file Trigonometry.h.

Here is the call graph for this function:

atan() [1/2]

template<typename FloatType >

FLOAT_T<FloatType> carl::atan ( const FLOAT_T< FloatType > &  _in )

inline

Definition at line 1492 of file FLOAT_T.h.

Here is the call graph for this function:

Here is the caller graph for this function:

atan() [2/2]

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

Interval<Number> carl::atan

(

const Interval< Number > &

i

)

Definition at line 70 of file Trigonometry.h.

Here is the call graph for this function:

Here is the caller graph for this function:

atan_assign()

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

void carl::atan_assign

(

Interval< Number > &

i

)

Definition at line 76 of file Trigonometry.h.

Here is the call graph for this function:

atanh()

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

Interval<Number> carl::atanh

(

const Interval< Number > &

i

)

Definition at line 142 of file Trigonometry.h.

Here is the call graph for this function:

Here is the caller graph for this function:

atanh_assign()

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

void carl::atanh_assign

(

Interval< Number > &

i

)

Definition at line 148 of file Trigonometry.h.

Here is the call graph for this function:

basename()

std::string carl::basename ( const std::string &  filename )

inline

Return the basename of a given filename.

Definition at line 33 of file logging_utils.h.

Here is the caller graph for this function:

binary()

template<typename T >

std::string carl::binary	(	const T &	a,
		const bool &	spacing = true
	)

Return the binary representation given value as bit string.

Note that this method is tailored to little endian systems.

Parameters

a	A value of any type
spacing	Specifies if the bytes shall be separated by a space.

Returns

Bit string representing a.

Definition at line 17 of file logging_utils.h.

bitsize() [1/9]

std::size_t carl::bitsize ( const cln::cl_I &  n )

inline

Get the bit size of the representation of a integer.

Parameters

n	An integer.

Returns

Bit size of n.

Definition at line 96 of file operations.h.

Here is the caller graph for this function:

bitsize() [2/9]

std::size_t carl::bitsize ( const cln::cl_RA &  n )

inline

Get the bit size of the representation of a fraction.

Parameters

n	A fraction.

Returns

Bit size of n.

Definition at line 104 of file operations.h.

Here is the call graph for this function:

bitsize() [3/9]

template<typename Number >

std::size_t carl::bitsize

(

const IntRepRealAlgebraicNumber< Number > &

n

)

Definition at line 332 of file Ran.h.

Here is the call graph for this function:

bitsize() [4/9]

std::size_t carl::bitsize ( const Monomial &  m )

inline

Returns

An approximation of the bitsize of this monomial.

Definition at line 10 of file Bitsize.h.

bitsize() [5/9]

std::size_t carl::bitsize ( const mpq_class &  n )

inline

Get the bit size of the representation of a fraction.

Parameters

n	A fraction.

Returns

Bit size of n.

Definition at line 104 of file operations.h.

Here is the call graph for this function:

bitsize() [6/9]

std::size_t carl::bitsize ( const mpz_class &  n )

inline

Get the bit size of the representation of a integer.

Parameters

n	An integer.

Returns

Bit size of n.

Definition at line 96 of file operations.h.

bitsize() [7/9]

template<typename Coeff , typename Ordering , typename Policies >

std::size_t carl::bitsize

(

const MultivariatePolynomial< Coeff, Ordering, Policies > &

p

)

Returns

An approximation of the bitsize of this polynomial.

Definition at line 27 of file Bitsize.h.

Here is the call graph for this function:

bitsize() [8/9]

template<typename Coeff >

std::size_t carl::bitsize

(

const Term< Coeff > &

t

)

Returns

An approximation of the bitsize of this term.

Definition at line 18 of file Bitsize.h.

Here is the call graph for this function:

bitsize() [9/9]

std::size_t carl::bitsize ( unsigned  )

inline

Definition at line 67 of file operations.h.

bitvector_variables() [1/2]

template<typename Pol >

void carl::bitvector_variables	(	const Formula< Pol > &	f,
		std::set< BVVariable > &	bvvs
	)

Definition at line 64 of file Variables.h.

Here is the call graph for this function:

bitvector_variables() [2/2]

template<typename T >

carlVariables carl::bitvector_variables ( const T &  t )

inline

Definition at line 254 of file Variables.h.

Here is the call graph for this function:

Here is the caller graph for this function:

boolean_variables()

template<typename T >

carlVariables carl::boolean_variables ( const T &  t )

inline

Definition at line 226 of file Variables.h.

Here is the call graph for this function:

bounds_connect()

template<typename Number >

bool carl::bounds_connect ( const UpperBound< Number > &  lhs, const LowerBound< Number > &  rhs  )

inline

Check whether the two bounds connect, for example as for ...3),[3...

Definition at line 74 of file operators.h.

Here is the caller graph for this function:

branching_point() [1/3]

template<typename Number >

Number carl::branching_point

(

const IntRepRealAlgebraicNumber< Number > &

n

)

Definition at line 241 of file Ran.h.

Here is the call graph for this function:

branching_point() [2/3]

template<typename Number , typename = std::enable_if_t<is_number_type<Number>::value>>

const Number& carl::branching_point

(

const Number &

n

)

Definition at line 13 of file NumberOperations.h.

branching_point() [3/3]

template<typename Number >

Number carl::branching_point

(

const RealAlgebraicNumberThom< Number > &

n

)

Definition at line 83 of file ran_thom.h.

callingFunction()

std::string carl::callingFunction

(

)

Definition at line 27 of file debug.cpp.

cauchyBound()

template<typename Coeff >

Coeff carl::cauchyBound

(

const UnivariatePolynomial< Coeff > &

p

)

Definition at line 19 of file RootBounds.h.

Here is the call graph for this function:

ceil() [1/9]

cln::cl_I carl::ceil ( const cln::cl_I &  n )

inline

Round up an integer.

Parameters

n	An integer.

Returns

.

Definition at line 300 of file operations.h.

ceil() [2/9]

cln::cl_I carl::ceil ( const cln::cl_RA &  n )

inline

Round up a fraction.

Parameters

n	A fraction.

Returns

.

Definition at line 291 of file operations.h.

ceil() [3/9]

template<typename FloatType >

FLOAT_T<FloatType> carl::ceil ( const FLOAT_T< FloatType > &  _in )

inline

Method which returns the next larger integer of the passed number or the number itself, if it is already an integer.

Parameters

_in

Number.

Returns

Number which holds the result.

Definition at line 1520 of file FLOAT_T.h.

Here is the call graph for this function:

Here is the caller graph for this function:

ceil() [4/9]

template<typename Number >

Interval<Number> carl::ceil ( const Interval< Number > &  _in )

inline

Method which returns the next larger integer of the passed number or the number itself, if it is already an integer.

Parameters

_in

Number.

Returns

Number which holds the result.

Definition at line 1535 of file Interval.h.

Here is the call graph for this function:

Here is the caller graph for this function:

ceil() [5/9]

template<typename Number >

Number carl::ceil

(

const IntRepRealAlgebraicNumber< Number > &

n

)

Definition at line 297 of file Ran.h.

Here is the call graph for this function:

ceil() [6/9]

mpz_class carl::ceil ( const mpq_class &  n )

inline

Definition at line 289 of file operations.h.

Here is the call graph for this function:

ceil() [7/9]

mpz_class carl::ceil ( const mpz_class &  n )

inline

Definition at line 295 of file operations.h.

ceil() [8/9]

template<typename Number >

Number carl::ceil

(

const RealAlgebraicNumberThom< Number > &

n

)

Definition at line 174 of file ran_thom.h.

ceil() [9/9]

double carl::ceil ( double  n )

inline

Definition at line 124 of file operations.h.

center()

template<typename Number >

Number carl::center

(

const Interval< Number > &

i

)

Returns the center point of the interval.

Returns

Center.

Definition at line 12 of file Sampling.h.

Here is the call graph for this function:

Here is the caller graph for this function:

charPol()

template<typename Coeff >

std::vector<Coeff> carl::charPol

(

const CoeffMatrix< Coeff > &

m

)

Definition at line 51 of file CharPol.h.

Here is the call graph for this function:

Here is the caller graph for this function:

CMakeOptions()

constexpr CMakeOptionPrinter carl::CMakeOptions ( bool  advanced = false )

constexprnoexcept

Definition at line 27 of file CompileInfo.h.

collectUFVars()

void carl::collectUFVars	(	std::set< UVariable > &	uvars,
		UFInstance	ufi
	)

Definition at line 12 of file UEquality.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

compare() [1/4]

template<typename Pol >

signed carl::compare	(	const BasicConstraint< Pol > &	_constraintA,
		const BasicConstraint< Pol > &	_constraintB
	)

Compares _constraintA with _constraintB.

Returns

2, if it is easy to decide that _constraintA and _constraintB have the same solutions. _constraintA = _constraintB 1, if it is easy to decide that _constraintB includes all solutions of _constraintA; _constraintA -> _constraintB -1, if it is easy to decide that _constraintA includes all solutions of _constraintB; _constraintB -> _constraintA -2, if it is easy to decide that _constraintA has no solution common with _constraintB; not(_constraintA and _constraintB) -3, if it is easy to decide that _constraintA and _constraintB can be intersected; _constraintA and _constraintB = _constraintC -4, if it is easy to decide that _constraintA is the inverse of _constraintB; _constraintA xor _constraintB 0, otherwise.

Definition at line 25 of file Comparison.h.

Here is the call graph for this function:

Here is the caller graph for this function:

compare() [2/4]

template<typename Pol >

auto carl::compare	(	const Constraint< Pol > &	c1,
		const Constraint< Pol > &	c2
	)

Definition at line 342 of file Constraint.h.

Here is the call graph for this function:

compare() [3/4]

template<typename Number >

bool carl::compare	(	const IntRepRealAlgebraicNumber< Number > &	lhs,
		const IntRepRealAlgebraicNumber< Number > &	rhs,
		const Relation	relation
	)

Definition at line 384 of file Ran.h.

Here is the call graph for this function:

compare() [4/4]

template<typename Number >

bool carl::compare	(	const IntRepRealAlgebraicNumber< Number > &	lhs,
		const Number &	rhs,
		const Relation	relation
	)

Definition at line 454 of file Ran.h.

Here is the call graph for this function:

complexity() [1/6]

template<typename Poly >

std::size_t carl::complexity

(

const BasicConstraint< Poly > &

c

)

Returns

An approximation of the complexity of this constraint.

Definition at line 11 of file Complexity.h.

Here is the call graph for this function:

Here is the caller graph for this function:

complexity() [2/6]

template<typename Pol >

size_t carl::complexity

(

const Formula< Pol > &

f

)

Definition at line 9 of file Complexity.h.

Here is the call graph for this function:

complexity() [3/6]

std::size_t carl::complexity ( const Monomial &  m )

inline

Returns

An approximation of the complexity of this monomial.

Definition at line 11 of file Complexity.h.

Here is the call graph for this function:

complexity() [4/6]

template<typename Coeff , typename Ordering , typename Policies >

std::size_t carl::complexity

(

const MultivariatePolynomial< Coeff, Ordering, Policies > &

p

)

Returns

An approximation of the complexity of this polynomial.

Definition at line 28 of file Complexity.h.

Here is the call graph for this function:

complexity() [5/6]

template<typename Coeff >

std::size_t carl::complexity

(

const Term< Coeff > &

t

)

Returns

An approximation of the complexity of this term.

Definition at line 19 of file Complexity.h.

Here is the call graph for this function:

complexity() [6/6]

template<typename Coeff >

std::size_t carl::complexity

(

const UnivariatePolynomial< Coeff > &

p

)

Returns

An approximation of the complexity of this polynomial.

Definition at line 38 of file Complexity.h.

Here is the call graph for this function:

computePolynomial() [1/2]

template<typename P >

P carl::computePolynomial

(

const FactorizedPolynomial< P > &

_fpoly

)

Obtains the polynomial (representation) of this factorized polynomial.

Note, that the result won't be stored in the factorized polynomial, hence, this method should only be called for debug purpose.

Parameters

_fpoly

The factorized polynomial to get its polynomial (representation) for.

Returns

The polynomial (representation) of this factorized polynomial

Here is the caller graph for this function:

computePolynomial() [2/2]

template<typename P >

P carl::computePolynomial

(

const PolynomialFactorizationPair< P > &

_pfPair

)

Compute the polynomial from the given polynomial-factorization pair.

Parameters

_fpPair

A polynomial-factorization pair.

Returns

The polynomial.

consistent_with() [1/2]

template<typename Pol >

static unsigned carl::consistent_with ( const BasicConstraint< Pol > &  c, const Assignment< Interval< double >> &  _solutionInterval  )

static

Checks whether this constraint is consistent with the given assignment from the its variables to interval domains.

Parameters

_solutionInterval

The interval domains of the variables.

Returns

1, if this constraint is consistent with the given intervals; 0, if this constraint is not consistent with the given intervals; 2, if it cannot be decided whether this constraint is consistent with the given intervals.

Definition at line 25 of file IntervalEvaluation.h.

Here is the call graph for this function:

consistent_with() [2/2]

template<typename Pol >

static unsigned carl::consistent_with ( const BasicConstraint< Pol > &  c, const Assignment< Interval< double >> &  _solutionInterval, Relation &  _stricterRelation  )

static

Checks whether this constraint is consistent with the given assignment from the its variables to interval domains.

Parameters

_solutionInterval	The interval domains of the variables.
_stricterRelation	This relation is set to a relation R such that this constraint and the given variable bounds imply the constraint formed by R, comparing this constraint's left-hand side to zero.

Returns

1, if this constraint is consistent with the given intervals; 0, if this constraint is not consistent with the given intervals; 2, if it cannot be decided whether this constraint is consistent with the given intervals.

Definition at line 124 of file IntervalEvaluation.h.

Here is the call graph for this function:

contained_in()

template<typename Number >

bool carl::contained_in	(	const IntRepRealAlgebraicNumber< Number > &	n,
		const Interval< Number > &	i
	)

Definition at line 373 of file Ran.h.

Here is the call graph for this function:

content()

template<typename Coeff >

Coeff carl::content

(

const UnivariatePolynomial< Coeff > &

p

)

The content of a polynomial is the gcd of the coefficients of the normal part of a polynomial.

The content of zero is zero.

See also

[3], page 53, definition 2.18

Returns

The content of the polynomial.

Definition at line 22 of file Content.h.

Here is the call graph for this function:

Here is the caller graph for this function:

convert() [1/9]

template<typename ToPoly , typename FromPoly , typename = std::enable_if_t<!needs_context_type<ToPoly>::value>>

BasicConstraint<ToPoly> carl::convert ( const BasicConstraint< FromPoly > &  c )

inline

Definition at line 13 of file Conversion.h.

Here is the call graph for this function:

convert() [2/9]

template<typename From , typename To , carl::DisableIf< std::is_same< From, To > > >

To carl::convert ( const From &  )

inline

Definition at line 8 of file conversion.h.

convert() [3/9]

template<typename From , typename To , carl::DisableIf< std::is_same< From, To > > = dummy>

Interval< To > carl::convert ( const Interval< From > &  i )

inline

Definition at line 9 of file Conversion.h.

Here is the call graph for this function:

convert() [4/9]

template<typename T , typename S , std::enable_if_t< is_polynomial_type< T >::value &&is_polynomial_type< S >::value &&!needs_context_type< T >::value, int > = 0>

T carl::convert ( const S &  r )

inline

Definition at line 106 of file Conversion.h.

Here is the call graph for this function:

convert() [5/9]

template<typename T , std::enable_if_t< is_ran_type< T >::value, int > = 0>

T carl::convert ( const T &  r )

inline

Definition at line 10 of file Conversion.h.

Here is the caller graph for this function:

convert() [6/9]

template<typename T , typename S , std::enable_if_t< is_polynomial_type< T >::value &&is_polynomial_type< S >::value &&needs_context_type< T >::value, int > = 0>

T carl::convert ( const typename T::ContextType &  c, const S &  r  )

inline

Definition at line 111 of file Conversion.h.

Here is the call graph for this function:

convert() [7/9]

template<typename ToPoly , typename FromPoly , typename = std::enable_if_t<needs_context_type<ToPoly>::value>>

BasicConstraint<ToPoly> carl::convert ( const typename ToPoly::ContextType &  context, const BasicConstraint< FromPoly > &  c  )

inline

Definition at line 9 of file Conversion.h.

Here is the call graph for this function:

Here is the caller graph for this function:

convert() [8/9]

template<typename ToPoly , typename FromPoly , typename = std::enable_if_t<needs_context_type<ToPoly>::value>>

VariableComparison<ToPoly> carl::convert ( const typename ToPoly::ContextType &  context, const VariableComparison< FromPoly > &  c  )

inline

Definition at line 9 of file Conversion.h.

Here is the call graph for this function:

convert() [9/9]

template<typename ToPoly , typename FromPoly , typename = std::enable_if_t<!needs_context_type<ToPoly>::value>>

VariableComparison<ToPoly> carl::convert ( const VariableComparison< FromPoly > &  c )

inline

Definition at line 30 of file Conversion.h.

Here is the call graph for this function:

convert< double, FLOAT_T< double > >()

template<>

FLOAT_T<double> carl::convert< double, FLOAT_T< double > > ( const double &  n )

inline

Definition at line 45 of file native.h.

convert< double, FLOAT_T< mpq_class > >()

template<>

FLOAT_T<mpq_class> carl::convert< double, FLOAT_T< mpq_class > > ( const double &  n )

inline

Definition at line 10 of file native.h.

Here is the call graph for this function:

convert< double, mpq_class >()

template<>

mpq_class carl::convert< double, mpq_class > ( const double &  n )

inline

Definition at line 5 of file native.h.

Here is the call graph for this function:

convert< FLOAT_T< double >, double >()

template<>

double carl::convert< FLOAT_T< double >, double > ( const FLOAT_T< double > &  n )

inline

Definition at line 45 of file native.h.

convert< FLOAT_T< double >, mpq_class >()

template<>

mpq_class carl::convert< FLOAT_T< double >, mpq_class > ( const FLOAT_T< double > &  n )

inline

Definition at line 30 of file native.h.

Here is the call graph for this function:

convert< FLOAT_T< mpq_class >, double >()

template<>

double carl::convert< FLOAT_T< mpq_class >, double > ( const FLOAT_T< mpq_class > &  n )

inline

Definition at line 20 of file native.h.

Here is the call graph for this function:

convert< FLOAT_T< mpq_class >, mpq_class >()

template<>

mpq_class carl::convert< FLOAT_T< mpq_class >, mpq_class > ( const FLOAT_T< mpq_class > &  n )

inline

Definition at line 35 of file native.h.

convert< mpq_class, double >()

template<>

double carl::convert< mpq_class, double > ( const mpq_class &  n )

inline

Definition at line 10 of file native.h.

convert< mpq_class, FLOAT_T< double > >()

template<>

FLOAT_T<double> carl::convert< mpq_class, FLOAT_T< double > > ( const mpq_class &  n )

inline

Definition at line 20 of file native.h.

convert< mpq_class, FLOAT_T< mpq_class > >()

template<>

FLOAT_T<mpq_class> carl::convert< mpq_class, FLOAT_T< mpq_class > > ( const mpq_class &  n )

inline

Definition at line 35 of file native.h.

convert_to_mvroot()

template<typename Poly >

MultivariateRoot<Poly> carl::convert_to_mvroot	(	const typename MultivariateRoot< Poly >::RAN &	ran,
		Variable	var
	)

Definition at line 130 of file MultivariateRoot.h.

Here is the call graph for this function:

coprimePart()

template<typename C , typename O , typename P >

MultivariatePolynomial<C,O,P> carl::coprimePart	(	const MultivariatePolynomial< C, O, P > &	p,
		const MultivariatePolynomial< C, O, P > &	q
	)

Calculates the coprime part of p and q.

Definition at line 15 of file CoprimePart.h.

Here is the call graph for this function:

cos() [1/5]

cln::cl_RA carl::cos ( const cln::cl_RA &  n )

inline

Definition at line 401 of file operations.h.

Here is the call graph for this function:

cos() [2/5]

template<typename FloatType >

FLOAT_T<FloatType> carl::cos ( const FLOAT_T< FloatType > &  _in )

inline

Definition at line 1468 of file FLOAT_T.h.

Here is the call graph for this function:

cos() [3/5]

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

Interval<Number> carl::cos

(

const Interval< Number > &

i

)

Definition at line 22 of file Trigonometry.h.

Here is the call graph for this function:

Here is the caller graph for this function:

cos() [4/5]

mpq_class carl::cos ( const mpq_class &  n )

inline

Definition at line 374 of file operations.h.

Here is the call graph for this function:

cos() [5/5]

double carl::cos ( double  in )

inline

Definition at line 157 of file operations.h.

Here is the caller graph for this function:

cos_assign()

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

void carl::cos_assign

(

Interval< Number > &

i

)

Definition at line 28 of file Trigonometry.h.

Here is the call graph for this function:

cosh()

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

Interval<Number> carl::cosh

(

const Interval< Number > &

i

)

Definition at line 94 of file Trigonometry.h.

Here is the call graph for this function:

Here is the caller graph for this function:

cosh_assign()

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

void carl::cosh_assign

(

Interval< Number > &

i

)

Definition at line 100 of file Trigonometry.h.

Here is the call graph for this function:

count_real_roots() [1/2]

template<typename Coefficient >

int carl::count_real_roots	(	const std::vector< UnivariatePolynomial< Coefficient >> &	seq,
		const Interval< Coefficient > &	i
	)

Calculate the number of real roots of a polynomial within a given interval based on a sturm sequence of this polynomial.

Parameters

seq	Sturm sequence.
i	Interval.

Returns

Number of real roots in the interval.

Definition at line 19 of file RootCounting.h.

Here is the call graph for this function:

Here is the caller graph for this function:

count_real_roots() [2/2]

template<typename Coefficient >

int carl::count_real_roots	(	const UnivariatePolynomial< Coefficient > &	p,
		const Interval< Coefficient > &	i
	)

Count the number of real roots of p within the given interval using Sturm sequences.

Parameters

p	The polynomial.
i	Count roots within this interval.

Returns

Number of real roots within the interval.

Definition at line 36 of file RootCounting.h.

Here is the call graph for this function:

createMonomial()

template<typename... T>

Monomial::Arg carl::createMonomial ( T &&...  t )

inline

Definition at line 168 of file MonomialPool.h.

Here is the caller graph for this function:

createSubstitution() [1/2]

template<typename Rational , typename Poly , typename Substitution , typename... Args>

ModelValue< Rational, Poly > carl::createSubstitution ( Args &&...  args )

inline

Definition at line 89 of file ModelSubstitution.h.

createSubstitution() [2/2]

template<typename Rational , typename Poly >

ModelValue< Rational, Poly > carl::createSubstitution ( const MultivariateRoot< Poly > &  mr )

inline

Definition at line 97 of file ModelSubstitution.h.

createSubstitutionPtr()

template<typename Rational , typename Poly , typename Substitution , typename... Args>

ModelSubstitutionPtr< Rational, Poly > carl::createSubstitutionPtr ( Args &&...  args )

inline

Definition at line 93 of file ModelSubstitution.h.

Here is the caller graph for this function:

defaultSortValue()

SortValue carl::defaultSortValue ( const Sort &  sort )

inline

Returns the default value for the given sort.

Parameters

sort	The sort to return the default value for.

Returns

The resulting sort value.

Definition at line 76 of file SortValueManager.h.

Here is the call graph for this function:

Here is the caller graph for this function:

defining_polynomial()

template<typename Poly , std::enable_if_t<!needs_context_type< Poly >::value, bool > = true>

Poly carl::defining_polynomial

(

const VariableComparison< Poly > &

f

)

Return a polynomial containing the lhs-variable that has a same root for the this lhs-variable as the value that rhs represent, e.g.

if this variable comparison is 'v < 3' then a defining polynomial could be 'v-3', because it has the same root for variable v, i.e., v=3.

Definition at line 138 of file VariableComparison.h.

Here is the call graph for this function:

Here is the caller graph for this function:

definiteness() [1/2]

template<typename C , typename O , typename P >

Definiteness carl::definiteness	(	const MultivariatePolynomial< C, O, P > &	p,
		bool	full_effort = true
	)

Definition at line 58 of file Definiteness.h.

Here is the call graph for this function:

definiteness() [2/2]

template<typename Coeff >

Definiteness carl::definiteness

(

const Term< Coeff > &

t

)

Definition at line 46 of file Definiteness.h.

Here is the call graph for this function:

Here is the caller graph for this function:

demangle()

std::string carl::demangle

(

const char *

name

)

Definition at line 19 of file debug.cpp.

Here is the caller graph for this function:

der()

template<typename Number >

std::list<MultivariatePolynomial<Number> > carl::der	(	const MultivariatePolynomial< Number > &	p,
		Variable::Arg	var,
		uint	from,
		uint	upto
	)

Definition at line 17 of file ThomUtil.h.

Here is the call graph for this function:

Here is the caller graph for this function:

derivative() [1/6]

std::pair<std::size_t,Monomial::Arg> carl::derivative ( const Monomial::Arg &  m, Variable  v, std::size_t  n = 1  )

inline

Computes the (partial) n'th derivative of this monomial with respect to the given variable.

Parameters

m	Monomial to derive.
v	Variable.
n	n.

Returns

Partial n'th derivative, consisting of constant factor and the remaining monomial.

Definition at line 35 of file Derivative.h.

Here is the call graph for this function:

derivative() [2/6]

template<typename C , typename O , typename P >

MultivariatePolynomial<C,O,P> carl::derivative	(	const MultivariatePolynomial< C, O, P > &	p,
		Variable	v,
		std::size_t	n = 1
	)

Computes the n'th derivative of p with respect to v.

Definition at line 86 of file Derivative.h.

Here is the call graph for this function:

derivative() [3/6]

template<typename T , EnableIf< is_number_type< T >> = dummy>

const T& carl::derivative	(	const T &	t,
		Variable	,
		std::size_t	n = 1
	)

Computes the n'th derivative of a number, which is either the number itself (for n = 0) or zero.

Definition at line 23 of file Derivative.h.

Here is the call graph for this function:

Here is the caller graph for this function:

derivative() [4/6]

template<typename C >

Term<C> carl::derivative	(	const Term< C > &	t,
		Variable	v,
		std::size_t	n = 1
	)

Computes the n'th derivative of t with respect to v.

Definition at line 72 of file Derivative.h.

Here is the call graph for this function:

derivative() [5/6]

template<typename C >

UnivariatePolynomial<C> carl::derivative	(	const UnivariatePolynomial< C > &	p,
		std::size_t	n = 1
	)

Computes the n'th derivative of p with respect to the main variable of p.

Definition at line 104 of file Derivative.h.

Here is the call graph for this function:

derivative() [6/6]

template<typename C >

UnivariatePolynomial<C> carl::derivative	(	const UnivariatePolynomial< C > &	p,
		Variable	v,
		std::size_t	n = 1
	)

Computes the n'th derivative of p with respect to v.

Definition at line 125 of file Derivative.h.

Here is the call graph for this function:

discriminant() [1/2]

template<typename Coeff , typename Ordering , typename Policies >

auto carl::discriminant ( const ContextPolynomial< Coeff, Ordering, Policies > &  p )

inline

Definition at line 17 of file Functions.h.

Here is the call graph for this function:

discriminant() [2/2]

template<typename Coeff >

UnivariatePolynomial<Coeff> carl::discriminant	(	const UnivariatePolynomial< Coeff > &	p,
		SubresultantStrategy	strategy = SubresultantStrategy::Default
	)

Definition at line 307 of file Resultant.h.

Here is the call graph for this function:

div() [1/7]

cln::cl_I carl::div ( const cln::cl_I &  a, const cln::cl_I &  b  )

inline

Divide two integers.

Asserts that the remainder is zero.

Parameters

a	First argument.
b	Second argument.

Returns

.

Definition at line 466 of file operations.h.

Here is the call graph for this function:

div() [2/7]

cln::cl_RA carl::div ( const cln::cl_RA &  a, const cln::cl_RA &  b  )

inline

Divide two fractions.

Parameters

a	First argument.
b	Second argument.

Returns

.

Definition at line 455 of file operations.h.

div() [3/7]

template<typename FloatType >

FLOAT_T<FloatType> carl::div ( const FLOAT_T< FloatType > &  _lhs, const FLOAT_T< FloatType > &  _rhs  )

inline

Implements the division which assumes that there is no remainder.

Parameters

_lhs
_rhs

Returns

Number which holds the result.

Definition at line 1365 of file FLOAT_T.h.

div() [4/7]

template<typename Number >

Interval<Number> carl::div ( const Interval< Number > &  _lhs, const Interval< Number > &  _rhs  )

inline

Implements the division which assumes that there is no remainder.

Parameters

_lhs
_rhs

Returns

Interval which holds the result.

Definition at line 1476 of file Interval.h.

Here is the call graph for this function:

div() [5/7]

mpq_class carl::div ( const mpq_class &  a, const mpq_class &  b  )

inline

Divide two fractions.

Parameters

a	First argument.
b	Second argument.

Returns

.

Definition at line 479 of file operations.h.

Here is the call graph for this function:

div() [6/7]

mpz_class carl::div ( const mpz_class &  a, const mpz_class &  b  )

inline

Divide two integers.

Asserts that the remainder is zero.

Parameters

a	First argument.
b	Second argument.

Returns

.

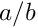Definition at line 490 of file operations.h.

Here is the call graph for this function:

div() [7/7]

sint carl::div ( sint  n, sint  m  )

inline

Definition at line 141 of file operations.h.

div_assign() [1/4]

cln::cl_I& carl::div_assign ( cln::cl_I &  a, const cln::cl_I &  b  )

inline

Divide two integers.

Asserts that the remainder is zero. Stores the result in the first argument.

Parameters

a	First argument.
b	Second argument.

Returns

.

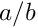Definition at line 491 of file operations.h.

Here is the call graph for this function:

div_assign() [2/4]

cln::cl_RA& carl::div_assign ( cln::cl_RA &  a, const cln::cl_RA &  b  )

inline

Divide two fractions.

Stores the result in the first argument.

Parameters

a	First argument.
b	Second argument.

Returns

.

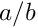Definition at line 478 of file operations.h.

div_assign() [3/4]

mpq_class& carl::div_assign ( mpq_class &  a, const mpq_class &  b  )

inline

Divide two integers.

Asserts that the remainder is zero. Stores the result in the first argument.

Parameters

a	First argument.
b	Second argument.

Returns

.

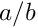Definition at line 515 of file operations.h.

Here is the call graph for this function:

div_assign() [4/4]

mpz_class& carl::div_assign ( mpz_class &  a, const mpz_class &  b  )

inline

Divide two integers.

Asserts that the remainder is zero. Stores the result in the first argument.

Parameters

a	First argument.
b	Second argument.

Returns

.

Definition at line 503 of file operations.h.

Here is the call graph for this function:

divide() [1/9]

void carl::divide ( const cln::cl_I &  dividend, const cln::cl_I &  divisor, cln::cl_I &  quotient, cln::cl_I &  remainder  )

inline

Definition at line 326 of file operations.h.

Here is the call graph for this function:

Here is the caller graph for this function:

divide() [2/9]

void carl::divide ( const mpz_class &  dividend, const mpz_class &  divisor, mpz_class &  quotient, mpz_class &  remainder  )

inline

Definition at line 469 of file operations.h.

Here is the call graph for this function:

divide() [3/9]

template<typename Coeff , typename Ordering , typename Policies >

DivisionResult<MultivariatePolynomial<Coeff,Ordering,Policies> > carl::divide	(	const MultivariatePolynomial< Coeff, Ordering, Policies > &	dividend,
		const MultivariatePolynomial< Coeff, Ordering, Policies > &	divisor
	)

Calculating the quotient and the remainder, such that for a given polynomial p we have p = divisor * quotient + remainder.

Parameters

divisor

Another polynomial

Returns

A divisionresult, holding the quotient and the remainder.

See also

Note

Division is only defined on fields

Definition at line 121 of file Division.h.

Here is the call graph for this function:

divide() [4/9]

template<typename Coeff , typename Ordering , typename Policies >

MultivariatePolynomial<Coeff,Ordering,Policies> carl::divide	(	const MultivariatePolynomial< Coeff, Ordering, Policies > &	p,
		const Coeff &	divisor
	)

Divides the polynomial by the given coefficient.

Applies if the coefficients are from a field.

Parameters

divisor

Returns

Definition at line 52 of file Division.h.

Here is the call graph for this function:

divide() [5/9]

template<typename Coeff >

Term<Coeff> carl::divide	(	const Term< Coeff > &	t,
		const Coeff &	c
	)

Definition at line 22 of file Division.h.

Here is the call graph for this function:

divide() [6/9]

template<typename Coeff >

DivisionResult<UnivariatePolynomial<Coeff> > carl::divide	(	const UnivariatePolynomial< Coeff > &	dividend,
		const UnivariatePolynomial< Coeff > &	divisor
	)

Divides the polynomial by another polynomial.

Parameters

dividend	Dividend.
divisor	Divisor.

Returns

dividend / divisor.

Definition at line 194 of file Division.h.

Here is the call graph for this function:

divide() [7/9]

template<typename Coeff >

DivisionResult<UnivariatePolynomial<Coeff> > carl::divide	(	const UnivariatePolynomial< Coeff > &	p,
		const Coeff &	divisor
	)

Definition at line 158 of file Division.h.

Here is the call graph for this function:

divide() [8/9]

template<typename Coeff >

DivisionResult<UnivariatePolynomial<Coeff> > carl::divide	(	const UnivariatePolynomial< Coeff > &	p,
		const typename UnderlyingNumberType< Coeff >::type &	divisor
	)

Definition at line 174 of file Division.h.

Here is the call graph for this function:

divide() [9/9]

void carl::divide ( sint  dividend, sint  divisor, sint &  quo, sint &  rem  )

inline

Definition at line 148 of file operations.h.

Here is the call graph for this function:

doNothing()

template<typename T >

void carl::doNothing	(	const T &	,
		const T &
	)

Definition at line 44 of file Cache.h.

eliminate_root()

template<typename Coeff >

void carl::eliminate_root	(	UnivariatePolynomial< Coeff > &	p,
		const Coeff &	root
	)

Reduces the polynomial such that the given root is not a root anymore.

The reduction is achieved by removing the linear factor (mainVar - root) from the polynomial, possibly multiple times.

This method assumes that the given root is an actual real root of this polynomial. If this is not the case, i.e. evaluate(root) != 0, the polynomial will contain meaningless garbage.

Parameters

p	The polynomial.
root	Root to be eliminated.

Definition at line 36 of file RootElimination.h.

Here is the call graph for this function:

Here is the caller graph for this function:

eliminate_zero_root()

template<typename Coeff >

void carl::eliminate_zero_root

(

UnivariatePolynomial< Coeff > &

p

)

Reduces the given polynomial such that zero is not a root anymore.

Is functionally equivalent to eliminate_root(0), but faster.

Definition at line 14 of file RootElimination.h.

Here is the call graph for this function:

Here is the caller graph for this function:

encode_as_constraints() [1/2]

template<typename Poly >

std::pair<std::vector<BasicConstraint<Poly> >, Variable> carl::encode_as_constraints	(	const MultivariateRoot< Poly > &	f,
		Assignment< typename VariableComparison< Poly >::RAN >	ass,
		EncodingCache< Poly >	cache
	)

Definition at line 48 of file Encoding.h.

Here is the call graph for this function:

Here is the caller graph for this function:

encode_as_constraints() [2/2]

template<typename Poly >

std::pair<std::vector<BasicConstraint<Poly> >, BasicConstraint<Poly> > carl::encode_as_constraints	(	const VariableComparison< Poly > &	f,
		const Assignment< typename VariableComparison< Poly >::RAN > &	ass,
		EncodingCache< Poly >	cache
	)

Definition at line 64 of file Encoding.h.

Here is the call graph for this function:

encode_as_constraints_simple()

template<typename Poly >

void carl::encode_as_constraints_simple	(	const MultivariateRoot< Poly > &	f,
		Assignment< typename VariableComparison< Poly >::RAN >	ass,
		Variable	var,
		std::vector< BasicConstraint< Poly >> &	out
	)

Definition at line 10 of file Encoding.h.

Here is the call graph for this function:

Here is the caller graph for this function:

encode_as_constraints_thom()

template<typename Poly >

void carl::encode_as_constraints_thom	(	const MultivariateRoot< Poly > &	f,
		Assignment< typename VariableComparison< Poly >::RAN >	ass,
		Variable	var,
		std::vector< BasicConstraint< Poly >> &	out
	)

Definition at line 28 of file Encoding.h.

Here is the call graph for this function:

Here is the caller graph for this function:

evaluate() [1/27]

template<typename Coeff , typename Ordering , typename Policies >

auto carl::evaluate	(	const BasicConstraint< ContextPolynomial< Coeff, Ordering, Policies >> &	p,
		const Assignment< typename ContextPolynomial< Coeff, Ordering, Policies >::RootType > &	a
	)

Definition at line 306 of file Evaluation.h.

Here is the call graph for this function:

evaluate() [2/27]

template<typename Number >

boost::tribool carl::evaluate	(	const BasicConstraint< MultivariatePolynomial< Number >> &	c,
		const Assignment< IntRepRealAlgebraicNumber< Number >> &	m,
		bool	refine_model = true,
		bool	use_root_bounds = true
	)

Definition at line 142 of file Evaluation.h.

Here is the call graph for this function:

evaluate() [3/27]

template<typename Number , typename Poly >

boost::tribool carl::evaluate ( const BasicConstraint< Poly > &  c, const Assignment< Interval< Number >> &  map  )

inline

Definition at line 12 of file IntervalEvaluation.h.

Here is the call graph for this function:

evaluate() [4/27]

template<typename Number , typename Poly , typename = std::enable_if_t<is_number_type<Number>::value>>

bool carl::evaluate	(	const BasicConstraint< Poly > &	c,
		const Assignment< Number > &	m
	)

Definition at line 10 of file Evaluation.h.

Here is the call graph for this function:

Here is the caller graph for this function:

evaluate() [5/27]

template<typename Number , typename Poly >

bool carl::evaluate	(	const BasicConstraint< Poly > &	c,
		std::map< Variable, RealAlgebraicNumberThom< Number >> &	m
	)

Definition at line 137 of file ran_thom.h.

evaluate() [6/27]

template<typename Coeff , typename Ordering , typename Policies >

auto carl::evaluate	(	const ContextPolynomial< Coeff, Ordering, Policies > &	p,
		const Assignment< typename ContextPolynomial< Coeff, Ordering, Policies >::RootType > &	a
	)

Definition at line 301 of file Evaluation.h.

Here is the call graph for this function:

evaluate() [7/27]

template<typename Coeff , typename Subst >

Subst carl::evaluate	(	const FactorizedPolynomial< Coeff > &	p,
		const std::map< Variable, Subst > &	substitutions
	)

Like substitute, but expects substitutions for all variables.

Returns

For a polynomial p, the function value p(x_1,...,x_n).

Definition at line 13 of file evaluation.h.

Here is the call graph for this function:

evaluate() [8/27]

template<typename P , typename Numeric >

Interval<Numeric> carl::evaluate	(	const FactorizedPolynomial< P > &	p,
		const std::map< Variable, Interval< Numeric >> &	map
	)

Definition at line 34 of file evaluation.h.

Here is the call graph for this function:

evaluate() [9/27]

template<typename Coefficient >

Coefficient carl::evaluate	(	const Monomial &	m,
		const std::map< Variable, Coefficient > &	substitutions
	)

Definition at line 11 of file Evaluation.h.

Here is the call graph for this function:

evaluate() [10/27]

template<typename Numeric >

Interval<Numeric> carl::evaluate ( const Monomial &  m, const std::map< Variable, Interval< Numeric >> &  map  )

inline

Definition at line 12 of file IntervalEvaluation.h.

Here is the call graph for this function:

evaluate() [11/27]

template<typename PolynomialType , typename Number , class strategy >

Interval<Number> carl::evaluate ( const MultivariateHorner< PolynomialType, strategy > &  mvH, const std::map< Variable, Interval< Number >> &  map  )

inline

Definition at line 15 of file IntervalEvaluation.h.

Here is the call graph for this function:

evaluate() [12/27]

template<typename C , typename O , typename P , typename SubstitutionType >

SubstitutionType carl::evaluate	(	const MultivariatePolynomial< C, O, P > &	p,
		const std::map< Variable, SubstitutionType > &	substitutions
	)

Like substitute, but expects substitutions for all variables.

Returns

For a polynomial p, the function value p(x_1,...,x_n).

Definition at line 37 of file Evaluation.h.

Here is the call graph for this function:

evaluate() [13/27]

template<typename Coeff , typename Policy , typename Ordering , typename Numeric >

Interval<Numeric> carl::evaluate ( const MultivariatePolynomial< Coeff, Policy, Ordering > &  p, const std::map< Variable, Interval< Numeric >> &  map  )

inline

Definition at line 47 of file IntervalEvaluation.h.

Here is the call graph for this function:

evaluate() [14/27]

template<typename Number >

Number carl::evaluate	(	const MultivariatePolynomial< Number > &	p,
		std::map< Variable, RealAlgebraicNumberThom< Number >> &	m
	)

Definition at line 88 of file ran_thom.h.

evaluate() [15/27]

template<typename Poly >

std::optional<typename MultivariateRoot<Poly>::RAN> carl::evaluate	(	const MultivariateRoot< Poly > &	mr,
		const carl::Assignment< typename MultivariateRoot< Poly >::RAN > &	m
	)

Return the emerging algebraic real after pluggin in a subpoint to replace all variables with algebraic reals that are not the root-variable "_z".

Parameters

m	must contain algebraic real assignments for all variables that are not "_z".

Returns

std::nullopt if the underlying polynomial has no root with index 'rootIdx' at the given subpoint.

Definition at line 152 of file MultivariateRoot.h.

Here is the call graph for this function:

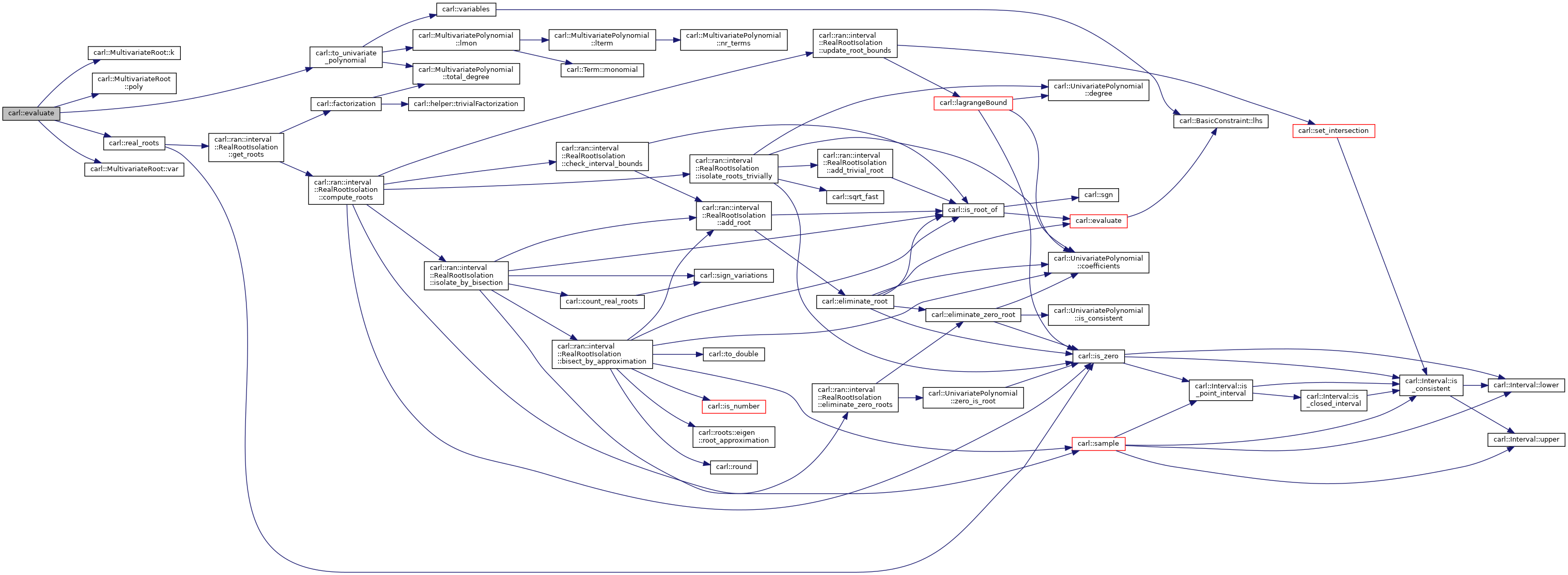
evaluate() [16/27]

template<typename Poly >

std::pair<typename SqrtEx<Poly>::Rational, bool> carl::evaluate	(	const SqrtEx< Poly > &	sqrt_ex,
		const std::map< Variable, typename SqrtEx< Poly >::Rational > &	eval_map,
		int	rounding
	)

Evaluates the square root expression.

Might be not exact when a square root is rounded.

Template Parameters

Poly

Parameters

sqrt_ex	The square root expression to be evaluated.
eval_map	Assignments for all variables.
rounding	-1 if square root should be rounded downwards, 1 if the square root should be rounded upwards, 0 if double precision is fine.

Returns

std::pair<SqrtEx<Poly>::Rational, bool> The first component is the evaluation result, the second indicates whether the result is exact (true) or rounded (false).

Definition at line 17 of file Evaluation.h.

Here is the call graph for this function:

evaluate() [17/27]

template<typename T , typename Rational , typename Poly >

ModelValue< Rational, Poly > carl::evaluate	(	const T &	t,
		const Model< Rational, Poly > &	m
	)

Evaluates a given expression t over a model.

The result is always a ModelValue, though it may be a ModelSubstitution in some cases.

Definition at line 47 of file ModelEvaluation.h.

Here is the call graph for this function:

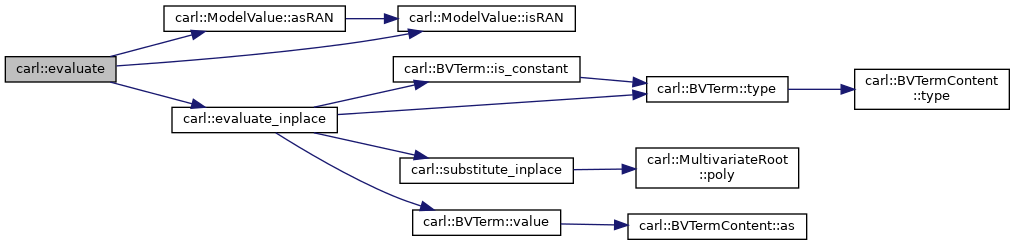
evaluate() [18/27]

template<typename T >

bool carl::evaluate ( const T &  t, Relation  r  )

inline

Definition at line 102 of file Relation.h.

Here is the call graph for this function:

evaluate() [19/27]

template<typename T1 , typename T2 >

bool carl::evaluate ( const T1 &  lhs, Relation  r, const T2 &  rhs  )

inline

Definition at line 107 of file Relation.h.

evaluate() [20/27]

template<typename Coeff , typename Numeric , EnableIf< std::is_same< Numeric, Coeff >> = dummy>

Interval<Numeric> carl::evaluate ( const Term< Coeff > &  t, const std::map< Variable, Interval< Numeric >> &  map  )

inline

Definition at line 29 of file IntervalEvaluation.h.

Here is the call graph for this function:

evaluate() [21/27]

template<typename Coefficient >

Coefficient carl::evaluate	(	const Term< Coefficient > &	t,
		const std::map< Variable, Coefficient > &	map
	)

Definition at line 24 of file Evaluation.h.

Here is the call graph for this function:

evaluate() [22/27]

template<typename Coeff >

Coeff carl::evaluate	(	const UnivariatePolynomial< Coeff > &	p,
		const Coeff &	value
	)

Definition at line 50 of file Evaluation.h.

Here is the call graph for this function:

evaluate() [23/27]

template<typename Numeric , typename Coeff , EnableIf< std::is_same< Numeric, Coeff >> = dummy>

Interval<Numeric> carl::evaluate ( const UnivariatePolynomial< Coeff > &  p, const std::map< Variable, Interval< Numeric >> &  map  )

inline

Definition at line 64 of file IntervalEvaluation.h.

Here is the call graph for this function:

evaluate() [24/27]

template<typename Poly >

boost::tribool carl::evaluate	(	const VariableComparison< Poly > &	f,
		const Assignment< typename VariableComparison< Poly >::RAN > &	a,
		bool	evaluate_non_welldef = false
	)

Definition at line 159 of file VariableComparison.h.

Here is the call graph for this function:

evaluate() [25/27]

template<typename Number >

boost::tribool carl::evaluate ( Interval< Number >  interval, Relation  relation  )

inline

Definition at line 10 of file Evaluation.h.

Here is the call graph for this function:

evaluate() [26/27]

template<typename Number >

std::optional<IntRepRealAlgebraicNumber<Number> > carl::evaluate	(	MultivariatePolynomial< Number >	p,
		const Assignment< IntRepRealAlgebraicNumber< Number >> &	m,
		bool	refine_model = true
	)

Evaluate the given polynomial with the given values for the variables.

Asserts that all variables of p have an assignment in m and that m has no additional assignments.

Returns std::nullopt if some unassigned variables are still contained in p after plugging in m.

Parameters

p	Polynomial to be evaluated
m	Variable assignment

Returns

Evaluation result

Definition at line 30 of file Evaluation.h.

Here is the call graph for this function:

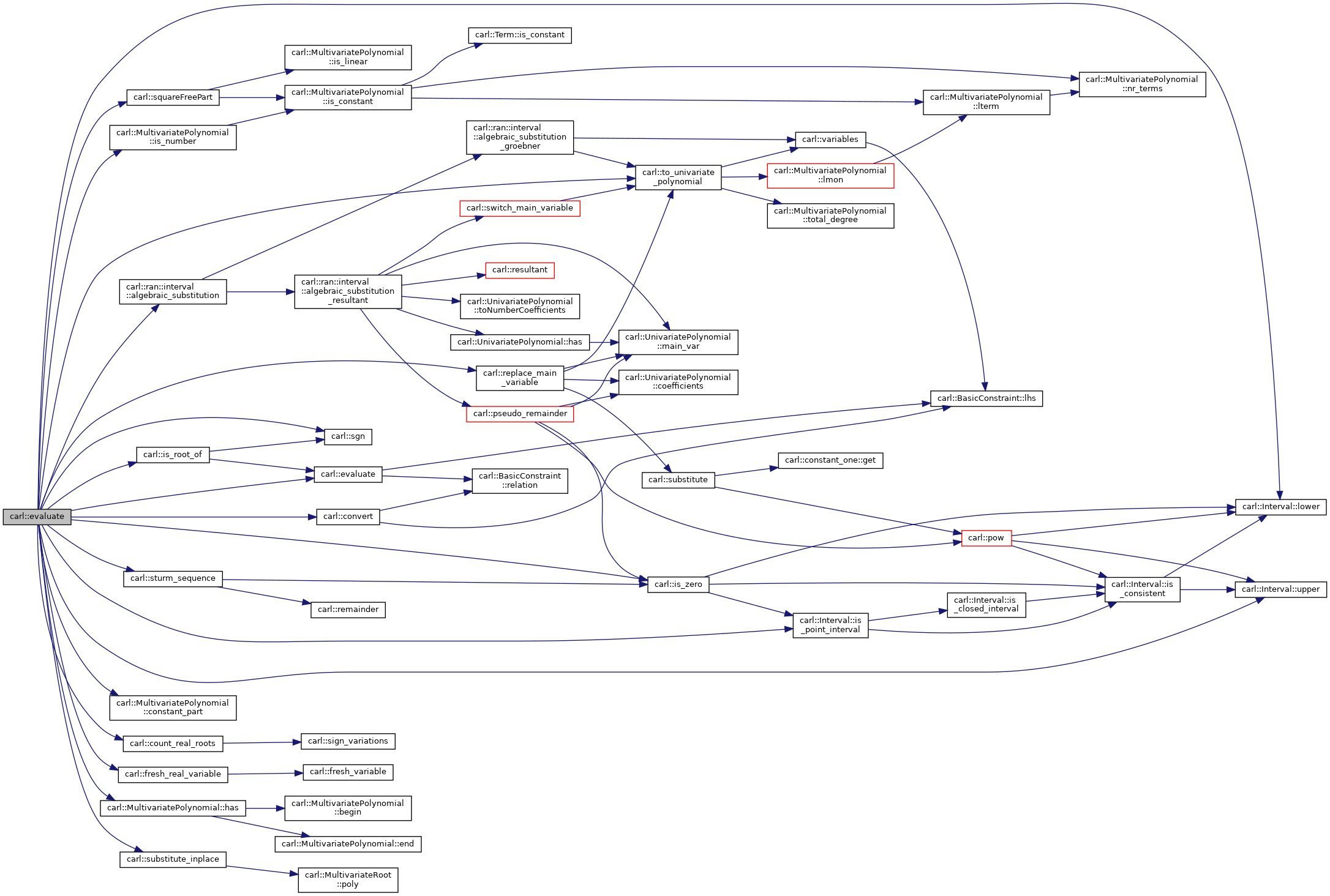
evaluate() [27/27]

bool carl::evaluate ( Sign  s, Relation  r  )

inline

Definition at line 86 of file Relation.h.

evaluate_inplace() [1/9]

template<typename Rational , typename Poly >

void carl::evaluate_inplace	(	ModelValue< Rational, Poly > &	res,
		BVConstraint &	bvc,
		const Model< Rational, Poly > &	m
	)

Evaluates a bitvector constraint to a ModelValue over a Model.

Definition at line 59 of file ModelEvaluation_Bitvector.h.

Here is the call graph for this function:

evaluate_inplace() [2/9]

template<typename Rational , typename Poly >

void carl::evaluate_inplace	(	ModelValue< Rational, Poly > &	res,
		BVTerm &	bvt,
		const Model< Rational, Poly > &	m
	)

Evaluates a bitvector term to a ModelValue over a Model.

Definition at line 45 of file ModelEvaluation_Bitvector.h.

Here is the call graph for this function:

Here is the caller graph for this function:

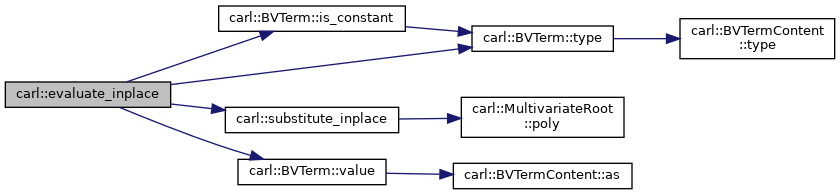
evaluate_inplace() [3/9]

template<typename Rational , typename Poly >

void carl::evaluate_inplace	(	ModelValue< Rational, Poly > &	res,
		const UEquality &	ue,
		const Model< Rational, Poly > &	m
	)

Evaluates a uninterpreted variable to a ModelValue over a Model.

Definition at line 50 of file ModelEvaluation_Uninterpreted.h.

Here is the call graph for this function:

evaluate_inplace() [4/9]

template<typename Rational , typename Poly >

void carl::evaluate_inplace	(	ModelValue< Rational, Poly > &	res,
		const UFInstance &	ufi,
		const Model< Rational, Poly > &	m
	)

Evaluates a uninterpreted function instance to a ModelValue over a Model.

Definition at line 24 of file ModelEvaluation_Uninterpreted.h.

Here is the call graph for this function:

evaluate_inplace() [5/9]

template<typename Rational , typename Poly >

void carl::evaluate_inplace	(	ModelValue< Rational, Poly > &	res,
		const UVariable &	uv,
		const Model< Rational, Poly > &	m
	)

Evaluates a uninterpreted variable to a ModelValue over a Model.

Definition at line 14 of file ModelEvaluation_Uninterpreted.h.

Here is the call graph for this function:

evaluate_inplace() [6/9]

template<typename Rational , typename Poly >

void carl::evaluate_inplace	(	ModelValue< Rational, Poly > &	res,
		Constraint< Poly > &	c,
		const Model< Rational, Poly > &	m
	)

Evaluates a constraint to a ModelValue over a Model.

If evaluation can not be done for some variables, the result may actually be a Constraint again.

Definition at line 25 of file ModelEvaluation_Constraint.h.

Here is the call graph for this function:

evaluate_inplace() [7/9]

template<typename Rational , typename Poly >

void carl::evaluate_inplace	(	ModelValue< Rational, Poly > &	res,
		Formula< Poly > &	f,
		const Model< Rational, Poly > &	m
	)

Evaluates a formula to a ModelValue over a Model.

If evaluation can not be done for some variables, the result may actually be a ModelPolynomialSubstitution.

Definition at line 199 of file ModelEvaluation_Formula.h.

Here is the call graph for this function:

evaluate_inplace() [8/9]

template<typename Rational , typename Poly >

void carl::evaluate_inplace	(	ModelValue< Rational, Poly > &	res,
		MultivariateRoot< Poly > &	mvr,
		const Model< Rational, Poly > &	m
	)

Evaluates a MultivariateRoot to a ModelValue over a Model.

If evaluation can not be done for some variables, the result may actually be a ModelMVRootSubstitution.

Definition at line 31 of file ModelEvaluation_MVRoot.h.

Here is the call graph for this function:

evaluate_inplace() [9/9]

template<typename Rational , typename Poly >

void carl::evaluate_inplace	(	ModelValue< Rational, Poly > &	res,
		Poly &	p,
		const Model< Rational, Poly > &	m
	)

Evaluates a polynomial to a ModelValue over a Model.

If evaluation can not be done for some variables, the result may actually be a ModelPolynomialSubstitution.

Definition at line 44 of file ModelEvaluation_Polynomial.h.

Here is the call graph for this function:

evaluateTE()

template<typename Number >

RealAlgebraicNumber<Number> carl::evaluateTE	(	const MultivariatePolynomial< Number > &	p,
		std::map< Variable, RealAlgebraicNumber< Number >> &	m
	)

Definition at line 18 of file ThomEvaluation.h.

Here is the call graph for this function:

exp()

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

Interval<Number> carl::exp

(

const Interval< Number > &

i

)

Definition at line 10 of file Exponential.h.

Here is the call graph for this function:

Here is the caller graph for this function:

exp_assign()

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

void carl::exp_assign

(

Interval< Number > &

i

)

Definition at line 16 of file Exponential.h.

Here is the call graph for this function:

extended_gcd()

template<typename Coeff >

UnivariatePolynomial<Coeff> carl::extended_gcd	(	const UnivariatePolynomial< Coeff > &	a,
		const UnivariatePolynomial< Coeff > &	b,
		UnivariatePolynomial< Coeff > &	s,
		UnivariatePolynomial< Coeff > &	t
	)

Calculates the extended greatest common divisor g of two polynomials.

The output polynomials s and t are computed such that .

Parameters

a	First polynomial.
b	Second polynomial.
s	First output polynomial.
t	Second output polynomial.

See also

[3], Algorithm 2.2

Returns

gcd(a,b)

Definition at line 39 of file GCD_univariate.h.

Here is the call graph for this function:

Here is the caller graph for this function:

extended_gcd_integer()

template<typename T >

T carl::extended_gcd_integer	(	T	a,
		T	b,
		T &	s,
		T &	t
	)

factorization() [1/2]

template<typename C , typename O , typename P >

Factors<MultivariatePolynomial<C,O,P> > carl::factorization	(	const MultivariatePolynomial< C, O, P > &	p,
		bool	includeConstants = true
	)

Try to factorize a multivariate polynomial.

Uses CoCoALib and GiNaC, if available, depending on the coefficient type of the polynomial.

Definition at line 31 of file Factorization.h.

Here is the call graph for this function:

Here is the caller graph for this function:

factorization() [2/2]

template<typename Coeff >

FactorMap<Coeff> carl::factorization

(

const UnivariatePolynomial< Coeff > &

p

)

Definition at line 325 of file Factorization_univariate.h.

Here is the call graph for this function:

factorizationsEqual()

template<typename P >

bool carl::factorizationsEqual	(	const Factorization< P > &	_factorizationA,
		const Factorization< P > &	_factorizationB
	)

factorizationToString()

template<typename P >

std::string carl::factorizationToString	(	const Factorization< P > &	_factorization,
		bool	_infix = true,
		bool	_friendlyVarNames = true
	)

fits_within()

template<typename T , typename T2 >

bool carl::fits_within

(

const T2 &

t

)

Definition at line 356 of file typetraits.h.

floor() [1/9]

cln::cl_I carl::floor ( const cln::cl_I &  n )

inline

Round down an integer.

Parameters

n	An integer.

Returns

.

Definition at line 282 of file operations.h.

floor() [2/9]

cln::cl_I carl::floor ( const cln::cl_RA &  n )

inline

Round down a fraction.

Parameters

n	A fraction.

Returns

.

Definition at line 273 of file operations.h.

floor() [3/9]

template<typename FloatType >

FLOAT_T<FloatType> carl::floor ( const FLOAT_T< FloatType > &  _in )

inline

Method which returns the next smaller integer of this number or the number itself, if it is already an integer.

Parameters

_in

Number.

Returns

Number which holds the result.

Definition at line 1506 of file FLOAT_T.h.

Here is the call graph for this function:

floor() [4/9]

template<typename Number >

Interval<Number> carl::floor ( const Interval< Number > &  _in )

inline

Method which returns the next smaller integer of this number or the number itself, if it is already an integer.

Parameters

_in

Number.

Returns

Number which holds the result.

Definition at line 1523 of file Interval.h.

Here is the call graph for this function:

Here is the caller graph for this function:

floor() [5/9]

template<typename Number >

Number carl::floor

(

const IntRepRealAlgebraicNumber< Number > &

n

)

Definition at line 293 of file Ran.h.

Here is the call graph for this function:

floor() [6/9]

mpz_class carl::floor ( const mpq_class &  n )

inline

Definition at line 278 of file operations.h.

Here is the call graph for this function:

floor() [7/9]

mpz_class carl::floor ( const mpz_class &  n )

inline

Definition at line 285 of file operations.h.

floor() [8/9]

template<typename Number >

Number carl::floor

(

const RealAlgebraicNumberThom< Number > &

n

)

Definition at line 170 of file ran_thom.h.

floor() [9/9]

double carl::floor ( double  n )

inline

Basic Operators.

The following functions implement simple operations on the given numbers.

Definition at line 121 of file operations.h.

formulaTypeToString()

std::string carl::formulaTypeToString ( FormulaType  _type )

inline

Parameters

_type

The formula type to get the string representation for.

Returns

The string representation of the given type.

Definition at line 63 of file FormulaContent.h.

Here is the caller graph for this function:

free_variables() [1/2]

template<typename Poly >

auto carl::free_variables

(

const Formula< Poly > &

f

)

Definition at line 173 of file PNF.h.

Here is the call graph for this function:

free_variables() [2/2]

template<typename Poly >

void carl::free_variables	(	const Formula< Poly > &	f,
		boost::container::flat_set< Variable > &	current_quantified_vars,
		boost::container::flat_set< Variable > &	free_vars
	)

Definition at line 116 of file PNF.h.

Here is the call graph for this function:

Here is the caller graph for this function:

fresh_bitvector_variable() [1/2]

Variable carl::fresh_bitvector_variable ( )

inlinenoexcept

Definition at line 186 of file VariablePool.h.

Here is the call graph for this function:

fresh_bitvector_variable() [2/2]

Variable carl::fresh_bitvector_variable ( const std::string &  name )

inline

Definition at line 189 of file VariablePool.h.

Here is the call graph for this function:

fresh_boolean_variable() [1/2]

Variable carl::fresh_boolean_variable ( )

inlinenoexcept

Definition at line 192 of file VariablePool.h.

Here is the call graph for this function:

Here is the caller graph for this function:

fresh_boolean_variable() [2/2]

Variable carl::fresh_boolean_variable ( const std::string &  name )

inline

Definition at line 195 of file VariablePool.h.

Here is the call graph for this function:

fresh_integer_variable() [1/2]

Variable carl::fresh_integer_variable ( )

inlinenoexcept

Definition at line 204 of file VariablePool.h.

Here is the call graph for this function:

Here is the caller graph for this function:

fresh_integer_variable() [2/2]

Variable carl::fresh_integer_variable ( const std::string &  name )

inline

Definition at line 207 of file VariablePool.h.

Here is the call graph for this function:

fresh_real_variable() [1/2]

Variable carl::fresh_real_variable ( )

inlinenoexcept

Definition at line 198 of file VariablePool.h.

Here is the call graph for this function:

Here is the caller graph for this function:

fresh_real_variable() [2/2]

Variable carl::fresh_real_variable ( const std::string &  name )

inline

Definition at line 201 of file VariablePool.h.

Here is the call graph for this function:

fresh_uninterpreted_variable() [1/2]

Variable carl::fresh_uninterpreted_variable ( )

inlinenoexcept

Definition at line 210 of file VariablePool.h.

Here is the call graph for this function:

fresh_uninterpreted_variable() [2/2]

Variable carl::fresh_uninterpreted_variable ( const std::string &  name )

inline

Definition at line 213 of file VariablePool.h.

Here is the call graph for this function:

fresh_variable() [1/2]

Variable carl::fresh_variable ( const std::string &  name, VariableType  vt  )

inline

Definition at line 182 of file VariablePool.h.

fresh_variable() [2/2]

Variable carl::fresh_variable ( VariableType  vt )

inlinenoexcept

Definition at line 179 of file VariablePool.h.

Here is the caller graph for this function:

from_int() [1/3]

template<typename To , typename From >

To carl::from_int ( const From &  n )

inline

from_int() [2/3]

template<>

mpq_class carl::from_int ( const sint &  n )

inline

Definition at line 153 of file operations.h.

from_int() [3/3]

template<>

mpq_class carl::from_int ( const uint &  n )

inline

Definition at line 148 of file operations.h.

gcd() [1/12]

cln::cl_I carl::gcd ( const cln::cl_I &  a, const cln::cl_I &  b  )

inline

Calculate the greatest common divisor of two integers.

Parameters

a	First argument.
b	Second argument.

Returns

Gcd of a and b.

Definition at line 310 of file operations.h.

Here is the call graph for this function:

Here is the caller graph for this function:

gcd() [2/12]

cln::cl_RA carl::gcd ( const cln::cl_RA &  a, const cln::cl_RA &  b  )

inline

Calculate the greatest common divisor of two fractions.

Asserts that the arguments are integral.

Parameters

a	First argument.
b	Second argument.

Returns

Gcd of a and b.

Definition at line 352 of file operations.h.

Here is the call graph for this function:

gcd() [3/12]

template<typename C , typename O , typename P >

Monomial::Arg carl::gcd	(	const Monomial::Arg &	a,
		const MultivariatePolynomial< C, O, P > &	b
	)

Definition at line 51 of file GCD.h.

Here is the call graph for this function:

gcd() [4/12]

Monomial::Arg carl::gcd	(	const Monomial::Arg &	lhs,
		const Monomial::Arg &	rhs
	)

Calculates the least common multiple of two monomial pointers.

If both are valid objects, the gcd of both is calculated. If only one is a valid object, this one is returned. If both are invalid objects, an empty monomial is returned.

Parameters

lhs	First monomial.
rhs	Second monomial.

Returns

gcd of lhs and rhs.

Definition at line 7 of file GCD_Monomial.cpp.

Here is the call graph for this function:

gcd() [5/12]

mpq_class carl::gcd ( const mpq_class &  a, const mpq_class &  b  )

inline

Definition at line 311 of file operations.h.

Here is the call graph for this function:

Here is the caller graph for this function:

gcd() [6/12]

mpz_class carl::gcd ( const mpz_class &  a, const mpz_class &  b  )

inline

Definition at line 299 of file operations.h.

gcd() [7/12]

template<typename C , typename O , typename P >

Monomial::Arg carl::gcd	(	const MultivariatePolynomial< C, O, P > &	a,
		const Monomial::Arg &	b
	)

Definition at line 37 of file GCD.h.

Here is the call graph for this function:

gcd() [8/12]

template<typename C , typename O , typename P >

MultivariatePolynomial< C, O, P > carl::gcd	(	const MultivariatePolynomial< C, O, P > &	a,
		const MultivariatePolynomial< C, O, P > &	b
	)

Definition at line 46 of file GCD_multivariate.h.

Here is the call graph for this function:

gcd() [9/12]

template<typename C , typename O , typename P >

Term<C> carl::gcd	(	const MultivariatePolynomial< C, O, P > &	a,
		const Term< C > &	b
	)

Definition at line 23 of file GCD.h.

Here is the call graph for this function:

gcd() [10/12]

template<typename C , typename O , typename P >

Term<C> carl::gcd	(	const Term< C > &	a,
		const MultivariatePolynomial< C, O, P > &	b
	)

Definition at line 32 of file GCD.h.

Here is the call graph for this function:

gcd() [11/12]

template<typename Coeff >

Term<Coeff> carl::gcd	(	const Term< Coeff > &	t1,
		const Term< Coeff > &	t2
	)

Calculates the gcd of (t1, t2).

If t1 or t2 is zero, undefined.

Parameters

t1	first term
t2	second term

Returns

gcd of t1 and t2.

Definition at line 17 of file GCD_Term.h.

Here is the call graph for this function:

gcd() [12/12]

template<typename Coeff >

UnivariatePolynomial<Coeff> carl::gcd	(	const UnivariatePolynomial< Coeff > &	a,
		const UnivariatePolynomial< Coeff > &	b
	)

Calculates the greatest common divisor of two polynomials.

Parameters

a	First polynomial.
b	Second polynomial.

Returns

gcd(a,b)

Definition at line 104 of file GCD_univariate.h.

Here is the call graph for this function:

gcd_assign() [1/4]

cln::cl_I& carl::gcd_assign ( cln::cl_I &  a, const cln::cl_I &  b  )

inline

Calculate the greatest common divisor of two integers.

Stores the result in the first argument.

Parameters

a	First argument.
b	Second argument.

Returns

Updated a.

Definition at line 321 of file operations.h.

Here is the call graph for this function:

gcd_assign() [2/4]

cln::cl_RA& carl::gcd_assign ( cln::cl_RA &  a, const cln::cl_RA &  b  )

inline

Calculate the greatest common divisor of two fractions.

Stores the result in the first argument. Asserts that the arguments are integral.

Parameters

a	First argument.
b	Second argument.

Returns

Updated a.

Definition at line 340 of file operations.h.

Here is the call graph for this function:

gcd_assign() [3/4]

mpq_class& carl::gcd_assign ( mpq_class &  a, const mpq_class &  b  )

inline

Calculate the greatest common divisor of two integers.

Stores the result in the first argument.

Parameters

a	First argument.
b	Second argument.

Returns

Updated a.

Definition at line 344 of file operations.h.

Here is the call graph for this function:

gcd_assign() [4/4]

mpz_class& carl::gcd_assign ( mpz_class &  a, const mpz_class &  b  )

inline

Calculate the greatest common divisor of two integers.

Stores the result in the first argument.

Parameters

a	First argument.
b	Second argument.

Returns

Updated a.

Definition at line 332 of file operations.h.

Here is the call graph for this function:

gcd_recursive()

template<typename Coeff >

UnivariatePolynomial<Coeff> carl::gcd_recursive	(	const UnivariatePolynomial< Coeff > &	a,
		const UnivariatePolynomial< Coeff > &	b
	)

Definition at line 12 of file GCD_univariate.h.

Here is the call graph for this function:

Here is the caller graph for this function:

get_assignment() [1/2]

template<typename Pol >

std::optional<std::pair<Variable, typename Pol::NumberType> > carl::get_assignment

(

const BasicConstraint< Pol > &

c

)

Definition at line 38 of file Substitution.h.

Here is the call graph for this function:

Here is the caller graph for this function:

get_assignment() [2/2]

template<typename Pol >

auto carl::get_assignment

(

const Constraint< Pol > &

c

)

Definition at line 340 of file Constraint.h.

Here is the call graph for this function:

get_denom() [1/4]

cln::cl_I carl::get_denom ( const cln::cl_RA &  n )

inline

Extract the denominator from a fraction.

Parameters

n

Fraction.

Returns

Denominator.

Definition at line 69 of file operations.h.

Here is the caller graph for this function:

get_denom() [2/4]

mpz_class carl::get_denom ( const FLOAT_T< mpq_class > &  _in )

inline

Implicitly converts the number to a rational and returns the denominator.

Parameters

_in

Number.

Returns

GMP interger which holds the result.

Definition at line 1578 of file FLOAT_T.h.

Here is the call graph for this function:

get_denom() [3/4]

mpz_class carl::get_denom ( const mpq_class &  n )

inline

Definition at line 75 of file operations.h.

get_denom() [4/4]

mpz_class carl::get_denom ( const mpz_class &  n )

inline

Definition at line 79 of file operations.h.

get_num() [1/4]

cln::cl_I carl::get_num ( const cln::cl_RA &  n )

inline

Extract the numerator from a fraction.

Parameters

n

Fraction.

Returns

Numerator.

Definition at line 60 of file operations.h.

Here is the caller graph for this function:

get_num() [2/4]

mpz_class carl::get_num ( const FLOAT_T< mpq_class > &  _in )

inline

Implicitly converts the number to a rational and returns the nominator.

Parameters

_in

Number.

Returns

GMP interger which holds the result.

Definition at line 1588 of file FLOAT_T.h.

Here is the call graph for this function:

get_num() [3/4]

mpz_class carl::get_num ( const mpq_class &  n )

inline

Definition at line 67 of file operations.h.

get_num() [4/4]

mpz_class carl::get_num ( const mpz_class &  n )

inline

Definition at line 71 of file operations.h.

get_other_bound_type()

static BoundType carl::get_other_bound_type ( BoundType  type )

inlinestatic

Definition at line 42 of file BoundType.h.

Here is the caller graph for this function:

get_ran_assignment() [1/2]

template<typename Rational , typename Poly >

std::optional<Assignment<typename Poly::RootType> > carl::get_ran_assignment	(	const carlVariables &	vars,
		const Model< Rational, Poly > &	model
	)

Definition at line 72 of file Assignment.h.

Here is the call graph for this function:

get_ran_assignment() [2/2]

template<typename Rational , typename Poly >

Assignment<typename Poly::RootType> carl::get_ran_assignment

(

const Model< Rational, Poly > &

model

)

Definition at line 88 of file Assignment.h.

get_strictest_bound_type()

static BoundType carl::get_strictest_bound_type ( BoundType  type1, BoundType  type2  )

inlinestatic

Definition at line 36 of file BoundType.h.

get_substitution() [1/2]

template<typename Pol >

std::optional<std::pair<Variable, Pol> > carl::get_substitution	(	const BasicConstraint< Pol > &	c,
		bool	_negated = false,
		Variable	_exclude = carl::Variable::NO_VARIABLE,
		std::optional< VarsInfo< Pol >>	var_info = std::nullopt
	)

If this constraint represents a substitution (equation, where at least one variable occurs only linearly), this method detects a (there could be various possibilities) corresponding substitution variable and term.

Parameters

_substitutionVariable	Is set to the substitution variable, if this constraint represents a substitution.
_substitutionTerm	Is set to the substitution term, if this constraint represents a substitution.

Returns

true, if this constraints represents a substitution; false, otherwise.

Definition at line 18 of file Substitution.h.

Here is the call graph for this function:

Here is the caller graph for this function:

get_substitution() [2/2]

template<typename Pol >

std::optional<std::pair<Variable, Pol> > carl::get_substitution	(	const Constraint< Pol > &	c,
		bool	_negated = false,
		Variable	_exclude = carl::Variable::NO_VARIABLE
	)

Definition at line 334 of file Constraint.h.

Here is the call graph for this function:

get_weakest_bound_type()

static BoundType carl::get_weakest_bound_type ( BoundType  type1, BoundType  type2  )

inlinestatic

Definition at line 31 of file BoundType.h.

getDefaultModel() [1/4]

template<typename Rational , typename Poly >

void carl::getDefaultModel	(	Model< Rational, Poly > &	_defaultModel,
		const BVTerm &	_constraint,
		bool	_overwrite = true,
		size_t	_seed = 0
	)

getDefaultModel() [2/4]

template<typename Rational , typename Poly >

void carl::getDefaultModel	(	Model< Rational, Poly > &	_defaultModel,
		const Constraint< Poly > &	_constraint,
		bool	_overwrite = true,
		size_t	_seed = 0
	)

getDefaultModel() [3/4]

template<typename Rational , typename Poly >

void carl::getDefaultModel	(	Model< Rational, Poly > &	_defaultModel,
		const Formula< Poly > &	_formula,
		bool	_overwrite = true,
		size_t	_seed = 0
	)

getDefaultModel() [4/4]

template<typename Rational , typename Poly >

void carl::getDefaultModel	(	Model< Rational, Poly > &	_defaultModel,
		const UEquality &	_constraint,
		bool	_overwrite = true,
		size_t	_seed = 0
	)

getRationalAssignmentsFromModel()

template<typename Rational , typename Poly >

bool carl::getRationalAssignmentsFromModel	(	const Model< Rational, Poly > &	_model,
		std::map< Variable, Rational > &	_rationalAssigns
	)

Obtains all assignments which can be transformed to rationals and stores them in the passed map.

Parameters

_model	The model from which to obtain the rational assignments.
_rationalAssigns	The map to store the rational assignments in.

Returns

true, if the entire model could be transformed to rational assignments. (not possible if, e.g., sqrt is contained)

getSort()

template<typename... Args>

Sort carl::getSort ( Args &&...  args )

inline

Gets the sort specified by the arguments.

Forwards to SortManager::getSort().

Definition at line 313 of file SortManager.h.

Here is the call graph for this function:

groebner_basis()

template<typename C , typename O , typename P >

std::vector<MultivariatePolynomial<C,O,P> > carl::groebner_basis

(

const std::vector< MultivariatePolynomial< C, O, P >> &

polys

)

Definition at line 11 of file Groebner.h.

handle_signal()

static void carl::handle_signal ( int  signal )

static

Actual signal handler.

Definition at line 44 of file debug.cpp.

Here is the caller graph for this function:

has_method_struct()

carl::has_method_struct

(

normalize

)

hash_add() [1/6]

template<typename First , typename... Tail>

void carl::hash_add ( std::size_t &  seed, const First &  value, Tail &&...  tail  )

inline

Variadic version of hash_add to add an arbitrary number of values to the seed.

Definition at line 61 of file hash.h.

Here is the call graph for this function:

hash_add() [2/6]

template<typename T1 , typename T2 >

void carl::hash_add ( std::size_t &  seed, const std::pair< T1, T2 > &  p  )

inline

Add hash of both elements of a std::pair to the seed.

Definition at line 39 of file hash.h.

Here is the call graph for this function:

hash_add() [3/6]

template<typename T >

void carl::hash_add ( std::size_t &  seed, const std::set< T > &  s  )

inline

Definition at line 53 of file hash.h.

Here is the call graph for this function:

hash_add() [4/6]

template<>

void carl::hash_add ( std::size_t &  seed, const std::size_t &  value  )

inline

Add hash of the given value to the hash seed.

Definition at line 31 of file hash.h.

Here is the call graph for this function:

hash_add() [5/6]

template<typename T >

void carl::hash_add ( std::size_t &  seed, const std::vector< T > &  v  )

inline

Add hash of all elements of a std::vector to the seed.

Definition at line 48 of file hash.h.

Here is the call graph for this function:

hash_add() [6/6]

template<typename T >

void carl::hash_add ( std::size_t &  seed, const T &  value  )

inline

Add hash of the given value to the hash seed.

Used hash_combine with the result of std::hash<T>.

Definition at line 23 of file hash.h.

Here is the call graph for this function:

Here is the caller graph for this function:

hash_all()

template<typename... Args>

std::size_t carl::hash_all ( Args &&...  args )

inline

Hashes an arbitrary number of values.

Uses hash_add with a seed of 0.

Definition at line 71 of file hash.h.

Here is the call graph for this function:

Here is the caller graph for this function:

hash_combine()

void carl::hash_combine ( std::size_t &  seed, std::size_t  value  )

inline

Add a value to the given hash seed.

This method is a copy of boost::hash_combine(). It is reimplemented here to avoid including all of boost/functional/hash.hpp for this single line of code.

Definition at line 14 of file hash.h.

Here is the caller graph for this function:

hash_value() [1/2]

template<typename Pol >

std::size_t carl::hash_value ( const carl::FormulaContent< Pol > &  content )

inline

Definition at line 26 of file FormulaPool.h.

Here is the call graph for this function:

hash_value() [2/2]

std::size_t carl::hash_value ( const carl::Monomial &  monomial )

inline

Definition at line 19 of file MonomialPool.h.

Here is the call graph for this function:

highestPower()

template<typename Number >

Number carl::highestPower ( const Number &  n )

inline

Returns the highest power of two below n.

Can also be seen as the highest bit set in n.

Parameters

n

Returns

Definition at line 192 of file operations.h.

Here is the caller graph for this function:

hirstMaceyBound()

template<typename Coeff >

Coeff carl::hirstMaceyBound

(

const UnivariatePolynomial< Coeff > &

p

)

Definition at line 35 of file RootBounds.h.

Here is the call graph for this function:

init()

int carl::init ( )

inline

The routine for initializing the carl library.

Which is called automatically by including this header. TODO prevent outside access.

Definition at line 31 of file initialize.h.

Here is the call graph for this function:

Here is the caller graph for this function:

initialize()

int carl::initialize ( )

inline

Method to ensure that upon inclusion, init() is called exactly once.

TODO prevent outside access.

Definition at line 49 of file initialize.h.

Here is the call graph for this function:

install_signal_handler()

static bool carl::install_signal_handler ( )

staticnoexcept

Installs the signal handler.

Definition at line 57 of file debug.cpp.

Here is the call graph for this function:

integer_below()

template<typename Number >

Number carl::integer_below ( const IntRepRealAlgebraicNumber< Number > &  n )

inline

Definition at line 312 of file Ran.h.

Here is the call graph for this function:

Here is the caller graph for this function:

integer_variables()

template<typename T >

carlVariables carl::integer_variables ( const T &  t )

inline

Definition at line 233 of file Variables.h.

Here is the call graph for this function:

invalid_enum_value()

template<typename Enum >

constexpr Enum carl::invalid_enum_value ( )

constexpr

Returns an enum value that is (most probably) not a valid enum value.

This can be used to check whether methods that take enums properly handle invalid values.

Definition at line 13 of file enum_util.h.

inverse() [1/2]

BVCompareRelation carl::inverse ( BVCompareRelation  _c )

inline

Definition at line 57 of file BVCompareRelation.h.

inverse() [2/2]

Relation carl::inverse ( Relation  r )

inline

Inverts the given relation symbol.

Definition at line 40 of file Relation.h.

Here is the caller graph for this function:

irreducible_factors() [1/2]

template<typename Coeff , typename Ordering , typename Policies >

auto carl::irreducible_factors ( const ContextPolynomial< Coeff, Ordering, Policies > &  p, bool  constants = true  )

inline

Definition at line 8 of file Functions.h.

Here is the call graph for this function:

Here is the caller graph for this function:

irreducible_factors() [2/2]

template<typename C , typename O , typename P >

std::vector<MultivariatePolynomial<C,O,P> > carl::irreducible_factors	(	const MultivariatePolynomial< C, O, P > &	p,
		bool	includeConstants = true
	)

Try to factorize a multivariate polynomial and return the irreducible factors (without multiplicities).

Uses CoCoALib and GiNaC, if available, depending on the coefficient type of the polynomial.

Definition at line 72 of file Factorization.h.

Here is the call graph for this function:

is_at_most_linear() [1/2]

bool carl::is_at_most_linear ( const Monomial &  m )

inline

Checks whether the monomial has at most degree one.

Returns

If monomial is linear or constant.

Definition at line 48 of file Degree.h.

Here is the call graph for this function:

Here is the caller graph for this function:

is_at_most_linear() [2/2]

template<typename Coeff >

bool carl::is_at_most_linear

(

const Term< Coeff > &

t

)

Checks whether the monomial has at most degree one.

Returns

If monomial is linear or constant.

Definition at line 102 of file Degree.h.

Here is the call graph for this function:

is_bound() [1/2]

template<typename Pol >

bool carl::is_bound

(

const BasicConstraint< Pol > &

constr

)

Returns

true, if this constraint is a bound.

Definition at line 11 of file Bound.h.

Here is the call graph for this function:

Here is the caller graph for this function:

is_bound() [2/2]

template<typename Pol >

bool carl::is_bound	(	const Constraint< Pol > &	constr,
		bool	negated = false
	)

Definition at line 346 of file Constraint.h.

Here is the call graph for this function:

is_constant() [1/5]

template<typename Coeff , typename Ordering , typename Policies >

bool carl::is_constant ( const ContextPolynomial< Coeff, Ordering, Policies > &  p )

inline

Definition at line 107 of file ContextPolynomial.h.

Here is the call graph for this function:

Here is the caller graph for this function:

is_constant() [2/5]

bool carl::is_constant ( const Monomial &  m )

inline

Checks whether the monomial is a constant.

Returns

If monomial is constant.

Definition at line 32 of file Degree.h.

Here is the call graph for this function:

is_constant() [3/5]

template<typename Coeff , typename Ordering , typename Policies >

bool carl::is_constant

(

const MultivariatePolynomial< Coeff, Ordering, Policies > &

p

)

Check if the polynomial is linear.

Definition at line 138 of file Degree.h.

Here is the call graph for this function:

is_constant() [4/5]

template<typename Coeff >

bool carl::is_constant

(

const Term< Coeff > &

t

)

Checks whether the monomial is a constant.

Returns

Definition at line 83 of file Degree.h.

Here is the call graph for this function:

is_constant() [5/5]

template<typename Coeff >

bool carl::is_constant

(

const UnivariatePolynomial< Coeff > &

p

)

Checks whether the polynomial is constant with respect to the main variable.

Returns

If polynomial is constant.

Definition at line 203 of file Degree.h.

Here is the call graph for this function:

is_integer() [1/10]

bool carl::is_integer ( const cln::cl_I &  )

inline

Check if a number is integral.

As cln::cl_I are always integral, this method returns true.

Returns

true.

Definition at line 78 of file operations.h.

is_integer() [2/10]

bool carl::is_integer ( const cln::cl_RA &  n )

inline

Check if a fraction is integral.

Parameters

n	A fraction.

Returns

true.

Definition at line 87 of file operations.h.

Here is the call graph for this function:

is_integer() [3/10]

template<typename FloatType >

bool carl::is_integer ( const FLOAT_T< FloatType > &  in )

inline

Definition at line 1354 of file FLOAT_T.h.

Here is the call graph for this function:

is_integer() [4/10]

template<typename IntegerT >

bool carl::is_integer ( const GFNumber< IntegerT > &  )

inline

Todo:

Implement this

Parameters

Definition at line 200 of file GFNumber.h.

is_integer() [5/10]

template<typename Number >

bool carl::is_integer ( const Interval< Number > &  n )

inline

Definition at line 1445 of file Interval.h.

Here is the call graph for this function:

Here is the caller graph for this function:

is_integer() [6/10]

template<typename Number >

bool carl::is_integer ( const IntRepRealAlgebraicNumber< Number > &  n )

inline

Definition at line 307 of file Ran.h.

Here is the call graph for this function:

is_integer() [7/10]

bool carl::is_integer ( const mpq_class &  n )

inline

Definition at line 83 of file operations.h.

is_integer() [8/10]

bool carl::is_integer ( const mpz_class &  )

inline

Definition at line 87 of file operations.h.

is_integer() [9/10]

bool carl::is_integer ( double  d )

inline

Definition at line 58 of file operations.h.

is_integer() [10/10]

bool carl::is_integer ( sint  )

inline

Definition at line 63 of file operations.h.

is_linear() [1/5]

template<typename Coeff , typename Ordering , typename Policies >

bool carl::is_linear ( const ContextPolynomial< Coeff, Ordering, Policies > &  p )

inline

Definition at line 117 of file ContextPolynomial.h.

Here is the call graph for this function:

Here is the caller graph for this function:

is_linear() [2/5]

bool carl::is_linear ( const Monomial &  m )

inline

Checks whether the monomial has exactly degree one.

Returns

If monomial is linear.

Definition at line 40 of file Degree.h.

Here is the call graph for this function:

is_linear() [3/5]

template<typename Coeff , typename Ordering , typename Policies >

bool carl::is_linear

(

const MultivariatePolynomial< Coeff, Ordering, Policies > &

p

)

Check if the polynomial is linear.

Definition at line 146 of file Degree.h.

Here is the call graph for this function:

is_linear() [4/5]

template<typename Coeff >

bool carl::is_linear

(

const Term< Coeff > &

t

)

Checks whether the monomial has exactly the degree one.

Returns

Definition at line 92 of file Degree.h.

Here is the call graph for this function:

is_linear() [5/5]

template<typename Coeff >

bool carl::is_linear

(

const UnivariatePolynomial< Coeff > &

p

)

Definition at line 208 of file Degree.h.

Here is the call graph for this function:

is_lower_bound() [1/2]

template<typename Pol >

bool carl::is_lower_bound

(

const BasicConstraint< Pol > &

constr

)

Returns

true, if this constraint is a lower bound.

Definition at line 21 of file Bound.h.

Here is the call graph for this function:

Here is the caller graph for this function:

is_lower_bound() [2/2]

template<typename Pol >

bool carl::is_lower_bound

(

const Constraint< Pol > &

constr

)

Definition at line 354 of file Constraint.h.

Here is the call graph for this function:

is_negative() [1/6]

bool carl::is_negative ( const cln::cl_I &  n )

inline

Definition at line 47 of file operations.h.

Here is the call graph for this function:

Here is the caller graph for this function:

is_negative() [2/6]

bool carl::is_negative ( const cln::cl_RA &  n )

inline

Definition at line 51 of file operations.h.

Here is the call graph for this function:

is_negative() [3/6]

bool carl::is_negative ( const mpq_class &  n )

inline

Definition at line 63 of file operations.h.

Here is the call graph for this function:

is_negative() [4/6]

bool carl::is_negative ( const mpz_class &  n )

inline

Definition at line 59 of file operations.h.

Here is the call graph for this function:

is_negative() [5/6]

template<typename T , EnableIf< has_is_negative< T >> >

bool carl::is_negative ( const T &  t )

inline

Definition at line 40 of file operations_generic.h.

is_negative() [6/6]

bool carl::is_negative ( double  n )

inline

Definition at line 35 of file operations.h.

is_number() [1/2]

template<typename Coeff , typename Ordering , typename Policies >

bool carl::is_number ( const ContextPolynomial< Coeff, Ordering, Policies > &  p )

inline

Definition at line 122 of file ContextPolynomial.h.

Here is the call graph for this function:

is_number() [2/2]

bool carl::is_number ( double  d )

inline

Definition at line 54 of file operations.h.

Here is the call graph for this function:

Here is the caller graph for this function:

is_one() [1/11]

bool carl::is_one ( const cln::cl_I &  n )

inline

Definition at line 31 of file operations.h.

Here is the call graph for this function:

is_one() [2/11]

bool carl::is_one ( const cln::cl_RA &  n )

inline

Definition at line 35 of file operations.h.

Here is the call graph for this function:

is_one() [3/11]

template<typename P >

bool carl::is_one

(

const FactorizedPolynomial< P > &

fp

)

Returns

true, if the factorized polynomial is one.

Definition at line 760 of file FactorizedPolynomial.h.

Here is the call graph for this function:

is_one() [4/11]

template<typename IntegerT >

bool carl::is_one

(

const GFNumber< IntegerT > &

_in

)

Definition at line 180 of file GFNumber.h.

Here is the call graph for this function:

is_one() [5/11]

template<typename Number >

bool carl::is_one

(

const Interval< Number > &

i

)

Check if this interval is a point-interval containing 1.

Definition at line 1462 of file Interval.h.

Here is the call graph for this function:

Here is the caller graph for this function:

is_one() [6/11]

bool carl::is_one ( const mpq_class &  n )

inline

Definition at line 47 of file operations.h.

Here is the call graph for this function:

is_one() [7/11]

bool carl::is_one ( const mpz_class &  n )

inline

Definition at line 43 of file operations.h.

Here is the call graph for this function:

is_one() [8/11]

template<typename C , typename O , typename P >

bool carl::is_one

(

const MultivariatePolynomial< C, O, P > &

p

)

Definition at line 589 of file MultivariatePolynomial.h.

Here is the call graph for this function:

is_one() [9/11]

template<typename T >

bool carl::is_one ( const T &  t )

inline

Definition at line 25 of file operations_generic.h.

is_one() [10/11]

template<typename Coeff >

bool carl::is_one ( const Term< Coeff > &  term )

inline

Checks whether a term is one.

Definition at line 315 of file Term.h.

Here is the call graph for this function:

is_one() [11/11]

template<typename Coefficient >

bool carl::is_one

(

const UnivariatePolynomial< Coefficient > &

p

)

Checks if the polynomial is equal to one.

Returns

If polynomial is one.

Definition at line 817 of file UnivariatePolynomial.h.

Here is the call graph for this function:

is_positive() [1/6]

bool carl::is_positive ( const cln::cl_I &  n )

inline

Definition at line 39 of file operations.h.

Here is the call graph for this function:

Here is the caller graph for this function:

is_positive() [2/6]

bool carl::is_positive ( const cln::cl_RA &  n )

inline

Definition at line 43 of file operations.h.

Here is the call graph for this function:

is_positive() [3/6]

bool carl::is_positive ( const mpq_class &  n )

inline

Definition at line 55 of file operations.h.

Here is the call graph for this function:

is_positive() [4/6]

bool carl::is_positive ( const mpz_class &  n )

inline

Definition at line 51 of file operations.h.

Here is the call graph for this function:

is_positive() [5/6]

template<typename T , EnableIf< has_is_positive< T >> >

bool carl::is_positive ( const T &  t )

inline

Definition at line 30 of file operations_generic.h.

is_positive() [6/6]

bool carl::is_positive ( double  n )

inline

Definition at line 31 of file operations.h.

is_root_of() [1/2]

template<typename Coeff >

bool carl::is_root_of	(	const UnivariatePolynomial< Coeff > &	p,
		const Coeff &	value
	)

Definition at line 62 of file Evaluation.h.

Here is the call graph for this function:

Here is the caller graph for this function:

is_root_of() [2/2]

template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>

Number carl::is_root_of	(	const UnivariatePolynomial< Number > &	p,
		const RAN &	value
	)

Definition at line 18 of file Operations.h.

Here is the call graph for this function:

is_strict()

bool carl::is_strict ( Relation  r )

inline

Definition at line 79 of file Relation.h.

Here is the caller graph for this function:

is_trivial()

template<typename C , typename O , typename P >

bool carl::is_trivial

(

const Factors< MultivariatePolynomial< C, O, P >> &

f

)

Definition at line 62 of file Factorization.h.

Here is the caller graph for this function:

is_upper_bound() [1/2]

template<typename Pol >

bool carl::is_upper_bound

(

const BasicConstraint< Pol > &

constr

)

Returns

true, if this constraint is an upper bound.

Definition at line 39 of file Bound.h.

Here is the call graph for this function:

Here is the caller graph for this function:

is_upper_bound() [2/2]

template<typename Pol >

bool carl::is_upper_bound

(

const Constraint< Pol > &

constr

)

Definition at line 356 of file Constraint.h.

Here is the call graph for this function:

is_weak()

bool carl::is_weak ( Relation  r )

inline

Definition at line 82 of file Relation.h.

Here is the call graph for this function:

Here is the caller graph for this function:

is_zero() [1/15]

bool carl::is_zero ( const cln::cl_I &  n )

inline

Definition at line 23 of file operations.h.

is_zero() [2/15]

bool carl::is_zero ( const cln::cl_RA &  n )

inline

Definition at line 27 of file operations.h.

is_zero() [3/15]

template<typename Coeff , typename Ordering , typename Policies >

bool carl::is_zero ( const ContextPolynomial< Coeff, Ordering, Policies > &  p )

inline

Definition at line 112 of file ContextPolynomial.h.

Here is the call graph for this function:

is_zero() [4/15]

template<typename P >

bool carl::is_zero

(

const FactorizedPolynomial< P > &

fp

)

Returns

true, if the factorized polynomial is zero.

Definition at line 768 of file FactorizedPolynomial.h.

Here is the call graph for this function:

is_zero() [5/15]

template<typename FloatType >

bool carl::is_zero ( const FLOAT_T< FloatType > &  _in )

inline

Definition at line 1594 of file FLOAT_T.h.

Here is the call graph for this function:

is_zero() [6/15]

template<typename IntegerT >

bool carl::is_zero

(

const GFNumber< IntegerT > &

_in

)

Definition at line 175 of file GFNumber.h.

Here is the call graph for this function:

is_zero() [7/15]

template<typename Number >

bool carl::is_zero

(

const Interval< Number > &

i

)

Check if this interval is a point-interval containing 0.

Definition at line 1453 of file Interval.h.

Here is the call graph for this function:

is_zero() [8/15]

template<typename Number >

bool carl::is_zero ( const IntRepRealAlgebraicNumber< Number > &  n )

inline

Definition at line 302 of file Ran.h.

Here is the call graph for this function:

is_zero() [9/15]

bool carl::is_zero ( const mpq_class &  n )

inline

Definition at line 39 of file operations.h.

Here is the call graph for this function:

is_zero() [10/15]

bool carl::is_zero ( const mpz_class &  n )

inline

Informational functions.

The following functions return informations about the given numbers.

Definition at line 35 of file operations.h.

Here is the call graph for this function:

is_zero() [11/15]

template<typename C , typename O , typename P >

bool carl::is_zero

(

const MultivariatePolynomial< C, O, P > &

p

)

Definition at line 593 of file MultivariatePolynomial.h.

Here is the call graph for this function:

is_zero() [12/15]

template<typename T >

bool carl::is_zero ( const T &  t )

inline

Definition at line 20 of file operations_generic.h.

is_zero() [13/15]

template<typename Coeff >

bool carl::is_zero ( const Term< Coeff > &  term )

inline

Checks whether a term is zero.

Definition at line 301 of file Term.h.

Here is the call graph for this function:

is_zero() [14/15]

template<typename Coefficient >

bool carl::is_zero

(

const UnivariatePolynomial< Coefficient > &

p

)

Checks if the polynomial is equal to zero.

Returns

If polynomial is zero.

Definition at line 808 of file UnivariatePolynomial.h.

Here is the call graph for this function:

is_zero() [15/15]

bool carl::is_zero ( double  n )

inline

Informational functions.

The following functions return informations about the given numbers.

Definition at line 27 of file operations.h.

isInf()

bool carl::isInf ( double  d )

inline

Definition at line 46 of file operations.h.

Here is the caller graph for this function:

isInfinity()

template<typename FloatType >

bool carl::isInfinity ( const FLOAT_T< FloatType > &  _in )

inline

Definition at line 1599 of file FLOAT_T.h.

Here is the call graph for this function:

isNan()

template<typename FloatType >

bool carl::isNan ( const FLOAT_T< FloatType > &  _in )

inline

Definition at line 1604 of file FLOAT_T.h.

Here is the call graph for this function:

isNaN()

bool carl::isNaN ( double  d )

inline

Definition at line 39 of file operations.h.

Here is the caller graph for this function:

isPartOf()

template<typename Rational , typename Poly >

bool carl::isPartOf	(	const std::map< Variable, Rational > &	_assignment,
		const Model< Rational, Poly > &	_model
	)

lagrangeBound()

template<typename Coeff >

Coeff carl::lagrangeBound

(

const UnivariatePolynomial< Coeff > &

p

)

Definition at line 55 of file RootBounds.h.

Here is the call graph for this function:

Here is the caller graph for this function:

lagrangeNegativeUpperBound()

template<typename Coeff >

Coeff carl::lagrangeNegativeUpperBound

(

const UnivariatePolynomial< Coeff > &

p

)

Computes an upper bound on the value of the negative real roots of the given univariate polynomial.

Note that the positive roots of P(-x) are the negative roots of P(x).

Definition at line 127 of file RootBounds.h.

Here is the call graph for this function:

Here is the caller graph for this function:

lagrangePositiveLowerBound()

template<typename Coeff >

Coeff carl::lagrangePositiveLowerBound

(

const UnivariatePolynomial< Coeff > &

p

)

Computes a lower bound on the value of the positive real roots of the given univariate polynomial.

Let . Then . Thus for any b it holds , that is, if b is an upper bound of the positive real roots of Q, then 1/b is a lower bound on the positive real roots of P. Note that the coefficients of Q are the ones of P in reverse order.

Definition at line 114 of file RootBounds.h.

Here is the call graph for this function:

Here is the caller graph for this function:

lagrangePositiveUpperBound()

template<typename Coeff >

Coeff carl::lagrangePositiveUpperBound

(

const UnivariatePolynomial< Coeff > &

p

)

Definition at line 84 of file RootBounds.h.

Here is the call graph for this function:

Here is the caller graph for this function:

lazyDiv()

template<typename C , typename O , typename P >

std::pair<MultivariatePolynomial<C,O,P>,MultivariatePolynomial<C,O,P> > carl::lazyDiv	(	const MultivariatePolynomial< C, O, P > &	_polyA,
		const MultivariatePolynomial< C, O, P > &	_polyB
	)

Definition at line 617 of file MultivariatePolynomial.h.

Here is the call graph for this function:

lcm() [1/5]

cln::cl_I carl::lcm ( const cln::cl_I &  a, const cln::cl_I &  b  )

inline

Calculate the least common multiple of two integers.

Parameters

a	First argument.
b	Second argument.

Returns

Lcm of a and b.

Definition at line 362 of file operations.h.

Here is the call graph for this function:

lcm() [2/5]

cln::cl_RA carl::lcm ( const cln::cl_RA &  a, const cln::cl_RA &  b  )

inline

Calculate the least common multiple of two fractions.

Asserts that the arguments are integral.

Parameters

a	First argument.
b	Second argument.

Returns

Lcm of a and b.

Definition at line 373 of file operations.h.

Here is the call graph for this function:

lcm() [3/5]

mpq_class carl::lcm ( const mpq_class &  a, const mpq_class &  b  )

inline

Definition at line 349 of file operations.h.

Here is the call graph for this function:

Here is the caller graph for this function:

lcm() [4/5]

mpz_class carl::lcm ( const mpz_class &  a, const mpz_class &  b  )

inline

Definition at line 305 of file operations.h.

lcm() [5/5]

template<typename C , typename O , typename P >

MultivariatePolynomial<C,O,P> carl::lcm	(	const MultivariatePolynomial< C, O, P > &	a,
		const MultivariatePolynomial< C, O, P > &	b
	)

Definition at line 8 of file LCM.h.

Here is the call graph for this function:

level_of()

template<typename Coeff , typename Ordering , typename Policies >

std::size_t carl::level_of ( const ContextPolynomial< Coeff, Ordering, Policies > &  p )

inline

Definition at line 127 of file ContextPolynomial.h.

Here is the call graph for this function:

log() [1/5]

cln::cl_RA carl::log ( const cln::cl_RA &  n )

inline

Definition at line 390 of file operations.h.

Here is the call graph for this function:

log() [2/5]

template<typename FloatType >

FLOAT_T<FloatType> carl::log ( const FLOAT_T< FloatType > &  _in )

inline

Method which returns the logarithm of the passed number.

Parameters

_in

Number.

Returns

Number which holds the result.

Definition at line 1425 of file FLOAT_T.h.

Here is the call graph for this function:

Here is the caller graph for this function:

log() [3/5]

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

Interval<Number> carl::log

(

const Interval< Number > &

i

)

Definition at line 22 of file Exponential.h.

Here is the call graph for this function:

Here is the caller graph for this function:

log() [4/5]

mpq_class carl::log ( const mpq_class &  n )

inline

Definition at line 363 of file operations.h.

Here is the call graph for this function:

log() [5/5]

double carl::log ( double  in )

inline

Definition at line 177 of file operations.h.

Here is the caller graph for this function:

log10() [1/3]

cln::cl_RA carl::log10 ( const cln::cl_RA &  n )

inline

Definition at line 393 of file operations.h.

Here is the call graph for this function:

log10() [2/3]

mpq_class carl::log10 ( const mpq_class &  n )

inline

Definition at line 366 of file operations.h.

Here is the call graph for this function:

log10() [3/3]

double carl::log10 ( double  in )

inline

Definition at line 180 of file operations.h.

Here is the caller graph for this function:

log_assign()

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

void carl::log_assign

(

Interval< Number > &

i

)

Definition at line 28 of file Exponential.h.

Here is the call graph for this function:

mod() [1/4]

cln::cl_I carl::mod ( const cln::cl_I &  a, const cln::cl_I &  b  )

inline

Calculate the remainder of the integer division.

Parameters

a	First argument.
b	Second argument.

Returns

.

Definition at line 445 of file operations.h.

Here is the caller graph for this function:

mod() [2/4]

mpz_class carl::mod ( const mpz_class &  n, const mpz_class &  m  )

inline

Definition at line 431 of file operations.h.

Here is the call graph for this function:

mod() [3/4]

sint carl::mod ( sint  n, sint  m  )

inline

Definition at line 134 of file operations.h.

Here is the caller graph for this function:

mod() [4/4]

uint carl::mod ( uint  n, uint  m  )

inline

Definition at line 131 of file operations.h.

multivariateTarskiQuery()

template<typename Number >

int carl::multivariateTarskiQuery	(	const MultivariatePolynomial< Number > &	Q,
		const MultiplicationTable< Number > &	table
	)

Definition at line 18 of file MultivariateTarskiQuery.h.

Here is the call graph for this function:

Here is the caller graph for this function:

newSortValue()

SortValue carl::newSortValue ( const Sort &  sort )

inline

Creates a new value for the given sort.

Parameters

sort	The sort to create a new value for.

Returns

The resulting sort value.

Definition at line 68 of file SortValueManager.h.

Here is the call graph for this function:

newtonSums()

template<typename Coeff >

std::vector<Coeff> carl::newtonSums

(

const std::vector< Coeff > &

newtonSums

)

Definition at line 18 of file CharPol.h.

Here is the caller graph for this function:

newUFInstance() [1/2]

UFInstance carl::newUFInstance ( const UninterpretedFunction &  uf, const std::vector< UTerm > &  args  )

inline

Gets the uninterpreted function instance with the given name, domain, arguments and codomain.

Parameters

uf	The underlying function of the uninterpreted function instance to get.
args	The arguments of the uninterpreted function instance to get.

Returns

The resulting uninterpreted function instance.

Definition at line 242 of file UFInstanceManager.h.

Here is the call graph for this function:

newUFInstance() [2/2]

UFInstance carl::newUFInstance ( const UninterpretedFunction &  uf, std::vector< UTerm > &&  args  )

inline

Gets the uninterpreted function instance with the given name, domain, arguments and codomain.

Parameters

uf	The underlying function of the uninterpreted function instance to get.
args	The arguments of the uninterpreted function instance to get.

Returns

The resulting uninterpreted function instance.

Definition at line 232 of file UFInstanceManager.h.

Here is the call graph for this function:

newUninterpretedFunction()

UninterpretedFunction carl::newUninterpretedFunction ( std::string  name, std::vector< Sort >  domain, Sort  codomain  )

inline

Gets the uninterpreted function with the given name, domain, arguments and codomain.

Parameters

name	The name of the uninterpreted function of the uninterpreted function to get.
domain	The domain of the uninterpreted function of the uninterpreted function to get.
codomain	The codomain of the uninterpreted function of the uninterpreted function to get.

Returns

The resulting uninterpreted function.

Definition at line 198 of file UFManager.h.

Here is the call graph for this function:

operator!=() [1/41]

template<typename P >

bool carl::operator!=	(	const BasicConstraint< P > &	lhs,
		const BasicConstraint< P > &	rhs
	)

Definition at line 112 of file BasicConstraint.h.

operator!=() [2/41]

template<typename C , typename O , typename P >

bool carl::operator!= ( const C &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the two arguments are not equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs != rhs

Definition at line 144 of file MultivariatePolynomial_operators.h.

operator!=() [3/41]

template<typename Coeff >

bool carl::operator!= ( const Coeff &  lhs, const Term< Coeff > &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 434 of file Term.h.

operator!=() [4/41]

template<typename P >

bool carl::operator!=	(	const Constraint< P > &	lhs,
		const Constraint< P > &	rhs
	)

Definition at line 293 of file Constraint.h.

operator!=() [5/41]

template<typename P >

bool carl::operator!= ( const FactorizedPolynomial< P > &  _lhs, const FactorizedPolynomial< P > &  _rhs  )

inline

Checks if the two arguments are not equal.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs != _rhs

operator!=() [6/41]

template<typename P >

bool carl::operator!= ( const FactorizedPolynomial< P > &  _lhs, const typename FactorizedPolynomial< P >::CoeffType &  _rhs  )

inline

Checks if the two arguments are not equal.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs != _rhs

Definition at line 827 of file FactorizedPolynomial.h.

operator!=() [7/41]

template<typename Number >

bool carl::operator!= ( const Interval< Number > &  lhs, const Interval< Number > &  rhs  )

inline

Operator for the comparison of two intervals.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

True if both intervals are unequal.

Definition at line 119 of file operators.h.

operator!=() [8/41]

template<typename Number >

bool carl::operator!= ( const Interval< Number > &  lhs, const Number &  rhs  )

inline

Definition at line 123 of file operators.h.

operator!=() [9/41]

bool carl::operator!= ( const Monomial::Arg &  lhs, const Monomial::Arg &  rhs  )

inline

Compares two arguments where one is a Monomial and the other is either a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 522 of file Monomial.h.

operator!=() [10/41]

template<typename C , typename O , typename P >

bool carl::operator!= ( const Monomial::Arg &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the two arguments are not equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs != rhs

Definition at line 136 of file MultivariatePolynomial_operators.h.

operator!=() [11/41]

template<typename Coeff >

bool carl::operator!= ( const Monomial::Arg &  lhs, const Term< Coeff > &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 426 of file Term.h.

operator!=() [12/41]

bool carl::operator!= ( const Monomial::Arg &  lhs, Variable  rhs  )

inline

Compares two arguments where one is a Monomial and the other is either a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 526 of file Monomial.h.

operator!=() [13/41]

template<typename C , typename O , typename P >

bool carl::operator!= ( const MultivariatePolynomial< C, O, P > &  lhs, const C &  rhs  )

inline

Checks if the two arguments are not equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs != rhs

Definition at line 128 of file MultivariatePolynomial_operators.h.

operator!=() [14/41]

template<typename C , typename O , typename P >

bool carl::operator!= ( const MultivariatePolynomial< C, O, P > &  lhs, const Monomial::Arg &  rhs  )

inline

Checks if the two arguments are not equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs != rhs

Definition at line 120 of file MultivariatePolynomial_operators.h.

operator!=() [15/41]

template<typename C , typename O , typename P >

bool carl::operator!= ( const MultivariatePolynomial< C, O, P > &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the two arguments are not equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs != rhs

Definition at line 112 of file MultivariatePolynomial_operators.h.

operator!=() [16/41]

template<typename C , typename O , typename P >

bool carl::operator!= ( const MultivariatePolynomial< C, O, P > &  lhs, const Term< C > &  rhs  )

inline

Checks if the two arguments are not equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs != rhs

Definition at line 116 of file MultivariatePolynomial_operators.h.

operator!=() [17/41]

template<typename C , typename O , typename P >

bool carl::operator!= ( const MultivariatePolynomial< C, O, P > &  lhs, const UnivariatePolynomial< C > &  rhs  )

inline

Checks if the two arguments are not equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs != rhs

Definition at line 153 of file MultivariatePolynomial_operators.h.

operator!=() [18/41]

template<typename C , typename O , typename P >

bool carl::operator!= ( const MultivariatePolynomial< C, O, P > &  lhs, const UnivariatePolynomial< MultivariatePolynomial< C >> &  rhs  )

inline

Checks if the two arguments are not equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs != rhs

Definition at line 161 of file MultivariatePolynomial_operators.h.

operator!=() [19/41]

template<typename C , typename O , typename P >

bool carl::operator!= ( const MultivariatePolynomial< C, O, P > &  lhs, Variable  rhs  )

inline

Checks if the two arguments are not equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs != rhs

Definition at line 124 of file MultivariatePolynomial_operators.h.

operator!=() [20/41]

template<typename N >

bool carl::operator!=	(	const N &	lhs,
		const ThomEncoding< N > &	rhs
	)

Definition at line 596 of file ThomEncoding.h.

operator!=() [21/41]

template<typename Number >

bool carl::operator!= ( const Number &  lhs, const Interval< Number > &  rhs  )

inline

Definition at line 127 of file operators.h.

operator!=() [22/41]

template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>

bool carl::operator!=	(	const Number &	lhs,
		const RAN &	rhs
	)

Definition at line 55 of file Operations.h.

operator!=() [23/41]

template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>

bool carl::operator!=	(	const RAN &	lhs,
		const Number &	rhs
	)

Definition at line 30 of file Operations.h.

Here is the call graph for this function:

operator!=() [24/41]

template<typename RAN , EnableIf< is_ran_type< RAN >> = dummy>

bool carl::operator!=	(	const RAN &	lhs,
		const RAN &	rhs
	)

Definition at line 80 of file Operations.h.

Here is the call graph for this function:

operator!=() [25/41]

template<typename Pol , bool AS>

bool carl::operator!=	(	const RationalFunction< Pol, AS > &	lhs,
		const RationalFunction< Pol, AS > &	rhs
	)

Definition at line 565 of file RationalFunction.h.

operator!=() [26/41]

template<typename C , typename O , typename P >

bool carl::operator!= ( const Term< C > &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the two arguments are not equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs != rhs

Definition at line 132 of file MultivariatePolynomial_operators.h.

operator!=() [27/41]

template<typename Coeff >

bool carl::operator!= ( const Term< Coeff > &  lhs, const Coeff &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 422 of file Term.h.

operator!=() [28/41]

template<typename Coeff >

bool carl::operator!= ( const Term< Coeff > &  lhs, const Monomial::Arg &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 414 of file Term.h.

operator!=() [29/41]

template<typename Coeff >

bool carl::operator!= ( const Term< Coeff > &  lhs, const Term< Coeff > &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 410 of file Term.h.

operator!=() [30/41]

template<typename Coeff >

bool carl::operator!= ( const Term< Coeff > &  lhs, Variable  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 418 of file Term.h.

operator!=() [31/41]

template<typename N >

bool carl::operator!=	(	const ThomEncoding< N > &	lhs,
		const N &	rhs
	)

Definition at line 583 of file ThomEncoding.h.

operator!=() [32/41]

template<typename N >

bool carl::operator!=	(	const ThomEncoding< N > &	lhs,
		const ThomEncoding< N > &	rhs
	)

Definition at line 569 of file ThomEncoding.h.

operator!=() [33/41]

template<typename P >

bool carl::operator!= ( const typename FactorizedPolynomial< P >::CoeffType &  _lhs, const FactorizedPolynomial< P > &  _rhs  )

inline

Checks if the two arguments are not equal.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs != _rhs

Definition at line 833 of file FactorizedPolynomial.h.

operator!=() [34/41]

bool carl::operator!= ( const UEquality &  lhs, const UEquality &  rhs  )

inline

Parameters

lhs	The left hand side.
rhs	The right hand side.

Returns

true, if lhs and rhs are not equal.

Definition at line 123 of file UEquality.h.

operator!=() [35/41]

template<typename C , typename O , typename P >

bool carl::operator!= ( const UnivariatePolynomial< C > &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the two arguments are not equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs != rhs

Definition at line 149 of file MultivariatePolynomial_operators.h.

operator!=() [36/41]

template<typename C , typename O , typename P >

bool carl::operator!= ( const UnivariatePolynomial< MultivariatePolynomial< C >> &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the two arguments are not equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs != rhs

Definition at line 157 of file MultivariatePolynomial_operators.h.

operator!=() [37/41]

bool carl::operator!=	(	const UTerm &	lhs,
		const UTerm &	rhs
	)

Definition at line 52 of file UTerm.cpp.

operator!=() [38/41]

bool carl::operator!= ( Sort  lhs, Sort  rhs  )

inline

Parameters

lhs	The left sort.
rhs	The right sort.

Returns

true, if the sorts are different.

Definition at line 78 of file Sort.h.

Here is the call graph for this function:

operator!=() [39/41]

bool carl::operator!= ( Variable  lhs, const Monomial::Arg &  rhs  )

inline

Compares two arguments where one is a Monomial and the other is either a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 530 of file Monomial.h.

operator!=() [40/41]

template<typename C , typename O , typename P >

bool carl::operator!= ( Variable  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the two arguments are not equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs != rhs

Definition at line 140 of file MultivariatePolynomial_operators.h.

operator!=() [41/41]

template<typename Coeff >

bool carl::operator!= ( Variable  lhs, const Term< Coeff > &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 430 of file Term.h.

operator%()

BVValue carl::operator% ( const BVValue &  lhs, const BVValue &  rhs  )

inline

Definition at line 171 of file BVValue.h.

Here is the call graph for this function:

operator&()

BVValue carl::operator& ( const BVValue &  lhs, const BVValue &  rhs  )

inline

Definition at line 179 of file BVValue.h.

Here is the call graph for this function:

operator*() [1/41]

template<typename Pol , bool AS>

RationalFunction<Pol, AS> carl::operator*	(	carl::sint	lhs,
		const RationalFunction< Pol, AS > &	rhs
	)

Definition at line 514 of file RationalFunction.h.

operator*() [2/41]

BVValue carl::operator*	(	const BVValue &	lhs,
		const BVValue &	rhs
	)

Definition at line 204 of file BVValue.cpp.

Here is the call graph for this function:

operator*() [3/41]

template<typename C , typename O , typename P >

auto carl::operator* ( const C &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Perform a multiplication involving a polynomial using operator*=().

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 654 of file MultivariatePolynomial_operators.h.

operator*() [4/41]

template<typename Coeff , EnableIf< carl::is_number_type< Coeff >> = dummy>

Term<Coeff> carl::operator* ( const Coeff &  lhs, const Monomial::Arg &  rhs  )

inline

Perform a multiplication involving a term.

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 586 of file Term.h.

operator*() [5/41]

template<typename Coeff >

Term<Coeff> carl::operator* ( const Coeff &  lhs, const Term< Coeff > &  rhs  )

inline

Perform a multiplication involving a term.

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 582 of file Term.h.

operator*() [6/41]

template<typename Coeff >

Term<Coeff> carl::operator* ( const Coeff &  lhs, Variable  rhs  )

inline

Perform a multiplication involving a term.

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 590 of file Term.h.

operator*() [7/41]

template<typename P >

FactorizedPolynomial<P> carl::operator*	(	const FactorizedPolynomial< P > &	_lhs,
		const FactorizedPolynomial< P > &	_rhs
	)

Perform a multiplication involving a polynomial.

Parameters

_lhs	Left hand side.
_rhs	Right hand side.

Returns

_lhs * _rhs

operator*() [8/41]

template<typename P >

FactorizedPolynomial<P> carl::operator*	(	const FactorizedPolynomial< P > &	_lhs,
		const typename FactorizedPolynomial< P >::CoeffType &	_rhs
	)

Perform a multiplication involving a polynomial.

Parameters

_lhs	Left hand side.
_rhs	Right hand side.

Returns

_lhs * _rhs

operator*() [9/41]

template<typename Number >

Interval<Number> carl::operator* ( const Interval< Number > &  lhs, const Interval< Number > &  rhs  )

inline

Operator for the multiplication of two intervals.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

Resulting interval.

Definition at line 386 of file operators.h.

Here is the call graph for this function:

operator*() [10/41]

template<typename Number >

Interval<Number> carl::operator* ( const Interval< Number > &  lhs, const Number &  rhs  )

inline

Operator for the multiplication of an interval and a number.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

Resulting interval.

Definition at line 397 of file operators.h.

Here is the call graph for this function:

operator*() [11/41]

template<typename Coeff , EnableIf< carl::is_number_type< Coeff >> = dummy>

Term<Coeff> carl::operator* ( const Monomial::Arg &  lhs, const Coeff &  rhs  )

inline

Perform a multiplication involving a term.

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 570 of file Term.h.

operator*() [12/41]

Monomial::Arg carl::operator*	(	const Monomial::Arg &	lhs,
		const Monomial::Arg &	rhs
	)

Perform a multiplication involving a monomial.

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 260 of file Monomial.cpp.

Here is the call graph for this function:

operator*() [13/41]

template<typename C , typename O , typename P >

auto carl::operator* ( const Monomial::Arg &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Perform a multiplication involving a polynomial using operator*=().

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 646 of file MultivariatePolynomial_operators.h.

operator*() [14/41]

template<typename Coeff >

Term<Coeff> carl::operator* ( const Monomial::Arg &  lhs, const Term< Coeff > &  rhs  )

inline

Perform a multiplication involving a term.

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 566 of file Term.h.

operator*() [15/41]

Monomial::Arg carl::operator*	(	const Monomial::Arg &	lhs,
		Variable	rhs
	)

Perform a multiplication involving a monomial.

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 309 of file Monomial.cpp.

Here is the call graph for this function:

operator*() [16/41]

mpq_class carl::operator* ( const mpq_class &  lhs, const mpq_class &  rhs  )

inline

Definition at line 526 of file operations.h.

operator*() [17/41]

template<typename C , typename O , typename P >

auto carl::operator* ( const MultivariatePolynomial< C, O, P > &  lhs, const C &  rhs  )

inline

Perform a multiplication involving a polynomial using operator*=().

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 638 of file MultivariatePolynomial_operators.h.

operator*() [18/41]

template<typename C , typename O , typename P >

auto carl::operator* ( const MultivariatePolynomial< C, O, P > &  lhs, const Monomial::Arg &  rhs  )

inline

Perform a multiplication involving a polynomial using operator*=().

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 630 of file MultivariatePolynomial_operators.h.

operator*() [19/41]

template<typename C , typename O , typename P >

auto carl::operator* ( const MultivariatePolynomial< C, O, P > &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Perform a multiplication involving a polynomial using operator*=().

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 622 of file MultivariatePolynomial_operators.h.

operator*() [20/41]

template<typename C , typename O , typename P >

auto carl::operator* ( const MultivariatePolynomial< C, O, P > &  lhs, const Term< C > &  rhs  )

inline

Perform a multiplication involving a polynomial using operator*=().

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 626 of file MultivariatePolynomial_operators.h.

operator*() [21/41]

template<typename C , typename O , typename P >

auto carl::operator* ( const MultivariatePolynomial< C, O, P > &  lhs, Variable  rhs  )

inline

Perform a multiplication involving a polynomial using operator*=().

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 634 of file MultivariatePolynomial_operators.h.

operator*() [22/41]

template<typename Number >

Interval<Number> carl::operator* ( const Number &  lhs, const Interval< Number > &  rhs  )

inline

Operator for the multiplication of an interval and a number.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

Resulting interval.

Definition at line 414 of file operators.h.

operator*() [23/41]

template<typename Pol , bool AS>

RationalFunction<Pol, AS> carl::operator*	(	const RationalFunction< Pol, AS > &	lhs,
		carl::sint	rhs
	)

Definition at line 509 of file RationalFunction.h.

operator*() [24/41]

template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>

RationalFunction<Pol, AS> carl::operator*	(	const RationalFunction< Pol, AS > &	lhs,
		const Monomial::Arg &	rhs
	)

Definition at line 489 of file RationalFunction.h.

operator*() [25/41]

template<typename Pol , bool AS>

RationalFunction<Pol, AS> carl::operator*	(	const RationalFunction< Pol, AS > &	lhs,
		const Pol &	rhs
	)

Definition at line 479 of file RationalFunction.h.

operator*() [26/41]

template<typename Pol , bool AS>

RationalFunction<Pol, AS> carl::operator*	(	const RationalFunction< Pol, AS > &	lhs,
		const RationalFunction< Pol, AS > &	rhs
	)

Definition at line 474 of file RationalFunction.h.

operator*() [27/41]

template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>

RationalFunction<Pol, AS> carl::operator*	(	const RationalFunction< Pol, AS > &	lhs,
		const Term< typename Pol::CoeffType > &	rhs
	)

Definition at line 484 of file RationalFunction.h.

operator*() [28/41]

template<typename Pol , bool AS>

RationalFunction<Pol, AS> carl::operator*	(	const RationalFunction< Pol, AS > &	lhs,
		const typename Pol::CoeffType &	rhs
	)

Definition at line 499 of file RationalFunction.h.

operator*() [29/41]

template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>

RationalFunction<Pol, AS> carl::operator*	(	const RationalFunction< Pol, AS > &	lhs,
		Variable	rhs
	)

Definition at line 494 of file RationalFunction.h.

operator*() [30/41]

template<typename C , typename O , typename P >

auto carl::operator* ( const Term< C > &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Perform a multiplication involving a polynomial using operator*=().

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 642 of file MultivariatePolynomial_operators.h.

operator*() [31/41]

template<typename P >

FactorizedPolynomial<P> carl::operator* ( const typename FactorizedPolynomial< P >::CoeffType &  _lhs, const FactorizedPolynomial< P > &  _rhs  )

inline

Perform a multiplication involving a polynomial.

Parameters

_lhs	Left hand side.
_rhs	Right hand side.

Returns

_lhs * _rhs

Definition at line 998 of file FactorizedPolynomial.h.

operator*() [32/41]

template<typename Pol , bool AS>

RationalFunction<Pol, AS> carl::operator*	(	const typename Pol::CoeffType &	lhs,
		const RationalFunction< Pol, AS > &	rhs
	)

Definition at line 504 of file RationalFunction.h.

operator*() [33/41]

template<typename Coeff >

Term<Coeff> carl::operator* ( Term< Coeff >  lhs, const Coeff &  rhs  )

inline

Perform a multiplication involving a term.

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 562 of file Term.h.

operator*() [34/41]

template<typename Coeff >

Term<Coeff> carl::operator* ( Term< Coeff >  lhs, const Monomial::Arg &  rhs  )

inline

Perform a multiplication involving a term.

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 554 of file Term.h.

operator*() [35/41]

template<typename Coeff >

Term<Coeff> carl::operator* ( Term< Coeff >  lhs, const Term< Coeff > &  rhs  )

inline

Perform a multiplication involving a term.

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 550 of file Term.h.

operator*() [36/41]

template<typename Coeff >

Term<Coeff> carl::operator* ( Term< Coeff >  lhs, Variable  rhs  )

inline

Perform a multiplication involving a term.

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 558 of file Term.h.

operator*() [37/41]

template<typename Coeff >

Term<Coeff> carl::operator* ( Variable  lhs, const Coeff &  rhs  )

inline

Perform a multiplication involving a term.

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 578 of file Term.h.

operator*() [38/41]

Monomial::Arg carl::operator*	(	Variable	lhs,
		const Monomial::Arg &	rhs
	)

Perform a multiplication involving a monomial.

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 338 of file Monomial.cpp.

operator*() [39/41]

template<typename C , typename O , typename P >

auto carl::operator* ( Variable  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Perform a multiplication involving a polynomial using operator*=().

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 650 of file MultivariatePolynomial_operators.h.

operator*() [40/41]

template<typename Coeff >

Term<Coeff> carl::operator* ( Variable  lhs, const Term< Coeff > &  rhs  )

inline

Perform a multiplication involving a term.

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 574 of file Term.h.

operator*() [41/41]

Monomial::Arg carl::operator*	(	Variable	lhs,
		Variable	rhs
	)

Perform a multiplication involving a monomial.

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 342 of file Monomial.cpp.

Here is the call graph for this function:

operator*=() [1/6]

template<typename Number >

Interval<Number>& carl::operator*= ( Interval< Number > &  lhs, const Interval< Number > &  rhs  )

inline

Operator for the multiplication of an interval and a number with assignment.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

Resulting interval.

Definition at line 425 of file operators.h.

Here is the call graph for this function:

operator*=() [2/6]

template<typename Number >

Interval<Number>& carl::operator*= ( Interval< Number > &  lhs, const Number &  rhs  )

inline

Operator for the multiplication of an interval and a number with assignment.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

Resulting interval.

Definition at line 437 of file operators.h.

Here is the call graph for this function:

operator*=() [3/6]

template<typename Coeff >

Term<Coeff>& carl::operator*=	(	Term< Coeff > &	lhs,
		const Coeff &	rhs
	)

Multiply a term with something and return the changed term.

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

Changed lhs.

Definition at line 333 of file Term.h.

Here is the call graph for this function:

operator*=() [4/6]

template<typename Coeff >

Term<Coeff>& carl::operator*=	(	Term< Coeff > &	lhs,
		const Monomial::Arg &	rhs
	)

Multiply a term with something and return the changed term.

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

Changed lhs.

Definition at line 354 of file Term.h.

Here is the call graph for this function:

operator*=() [5/6]

template<typename Coeff >

Term<Coeff>& carl::operator*=	(	Term< Coeff > &	lhs,
		const Term< Coeff > &	rhs
	)

Multiply a term with something and return the changed term.

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

Changed lhs.

Definition at line 366 of file Term.h.

Here is the call graph for this function:

operator*=() [6/6]

template<typename Coeff >

Term<Coeff>& carl::operator*=	(	Term< Coeff > &	lhs,
		Variable	rhs
	)

Multiply a term with something and return the changed term.

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

Changed lhs.

Definition at line 342 of file Term.h.

Here is the call graph for this function:

operator+() [1/34]

BVValue carl::operator+	(	const BVValue &	lhs,
		const BVValue &	rhs
	)

Definition at line 193 of file BVValue.cpp.

Here is the call graph for this function:

operator+() [2/34]

template<typename C , EnableIf< carl::is_number_type< C >> = dummy>

auto carl::operator+ ( const C &  lhs, const Monomial::Arg &  rhs  )

inline

Performs an addition involving a polynomial using operator+=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs + rhs

Definition at line 514 of file MultivariatePolynomial_operators.h.

operator+() [3/34]

template<typename C , typename O , typename P >

auto carl::operator+ ( const C &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Performs an addition involving a polynomial using operator+=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs + rhs

Definition at line 506 of file MultivariatePolynomial_operators.h.

operator+() [4/34]

template<typename C >

auto carl::operator+ ( const C &  lhs, const Term< C > &  rhs  )

inline

Performs an addition involving a polynomial using operator+=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs + rhs

Definition at line 510 of file MultivariatePolynomial_operators.h.

operator+() [5/34]

template<typename C , EnableIf< carl::is_number_type< C >> = dummy>

auto carl::operator+ ( const C &  lhs, Variable  rhs  )

inline

Performs an addition involving a polynomial using operator+=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs + rhs

Definition at line 518 of file MultivariatePolynomial_operators.h.

operator+() [6/34]

template<typename P >

FactorizedPolynomial<P> carl::operator+	(	const FactorizedPolynomial< P > &	_lhs,
		const FactorizedPolynomial< P > &	_rhs
	)

Performs an addition involving a polynomial.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs + _rhs

operator+() [7/34]

template<typename P >

FactorizedPolynomial<P> carl::operator+	(	const FactorizedPolynomial< P > &	_lhs,
		const typename FactorizedPolynomial< P >::CoeffType &	_rhs
	)

Performs an addition involving a polynomial.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs + _rhs

operator+() [8/34]

template<typename Number >

Interval<Number> carl::operator+ ( const Interval< Number > &  lhs, const Interval< Number > &  rhs  )

inline

Operator for the addition of two intervals.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

Resulting interval.

Definition at line 261 of file operators.h.

Here is the call graph for this function:

operator+() [9/34]

template<typename Number >

Interval<Number> carl::operator+ ( const Interval< Number > &  lhs, const Number &  rhs  )

inline

Operator for the addition of an interval and a number.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

Resulting interval.

Definition at line 272 of file operators.h.

Here is the call graph for this function:

operator+() [10/34]

template<typename C , EnableIf< carl::is_number_type< C >> = dummy>

auto carl::operator+ ( const Monomial::Arg &  lhs, const C &  rhs  )

inline

Performs an addition involving a polynomial using operator+=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs + rhs

Definition at line 490 of file MultivariatePolynomial_operators.h.

operator+() [11/34]

template<typename C , typename O , typename P >

auto carl::operator+ ( const Monomial::Arg &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Performs an addition involving a polynomial using operator+=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs + rhs

Definition at line 482 of file MultivariatePolynomial_operators.h.

operator+() [12/34]

template<typename C >

auto carl::operator+ ( const Monomial::Arg &  lhs, const Term< C > &  rhs  )

inline

Performs an addition involving a polynomial using operator+=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs + rhs

Definition at line 486 of file MultivariatePolynomial_operators.h.

operator+() [13/34]

template<typename C , typename O , typename P >

auto carl::operator+ ( const MultivariatePolynomial< C, O, P > &  lhs, const C &  rhs  )

inline

Performs an addition involving a polynomial using operator+=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs + rhs

Definition at line 458 of file MultivariatePolynomial_operators.h.

operator+() [14/34]

template<typename C , typename O , typename P >

auto carl::operator+ ( const MultivariatePolynomial< C, O, P > &  lhs, const Monomial::Arg &  rhs  )

inline

Performs an addition involving a polynomial using operator+=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs + rhs

Definition at line 450 of file MultivariatePolynomial_operators.h.

operator+() [15/34]

template<typename C , typename O , typename P >

auto carl::operator+ ( const MultivariatePolynomial< C, O, P > &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Performs an addition involving a polynomial using operator+=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs + rhs

Definition at line 442 of file MultivariatePolynomial_operators.h.

operator+() [16/34]

template<typename C , typename O , typename P >

auto carl::operator+ ( const MultivariatePolynomial< C, O, P > &  lhs, const Term< C > &  rhs  )

inline

Performs an addition involving a polynomial using operator+=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs + rhs

Definition at line 446 of file MultivariatePolynomial_operators.h.

operator+() [17/34]

template<typename C , typename O , typename P >

auto carl::operator+ ( const MultivariatePolynomial< C, O, P > &  lhs, Variable  rhs  )

inline

Performs an addition involving a polynomial using operator+=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs + rhs

Definition at line 454 of file MultivariatePolynomial_operators.h.

operator+() [18/34]

template<typename N >

ThomEncoding<N> carl::operator+	(	const N &	lhs,
		const ThomEncoding< N > &	rhs
	)

Definition at line 599 of file ThomEncoding.h.

operator+() [19/34]

template<typename Number >

Interval<Number> carl::operator+ ( const Number &  lhs, const Interval< Number > &  rhs  )

inline

Operator for the addition of an interval and a number.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

Resulting interval.

Definition at line 283 of file operators.h.

operator+() [20/34]

template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>

RationalFunction<Pol, AS> carl::operator+	(	const RationalFunction< Pol, AS > &	lhs,
		const Monomial::Arg &	rhs
	)

Definition at line 424 of file RationalFunction.h.

operator+() [21/34]

template<typename Pol , bool AS>

RationalFunction<Pol, AS> carl::operator+	(	const RationalFunction< Pol, AS > &	lhs,
		const Pol &	rhs
	)

Definition at line 414 of file RationalFunction.h.

operator+() [22/34]

template<typename Pol , bool AS>

RationalFunction<Pol, AS> carl::operator+	(	const RationalFunction< Pol, AS > &	lhs,
		const RationalFunction< Pol, AS > &	rhs
	)

Definition at line 409 of file RationalFunction.h.

operator+() [23/34]

template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>

RationalFunction<Pol, AS> carl::operator+	(	const RationalFunction< Pol, AS > &	lhs,
		const Term< typename Pol::CoeffType > &	rhs
	)

Definition at line 419 of file RationalFunction.h.

operator+() [24/34]

template<typename Pol , bool AS>

RationalFunction<Pol, AS> carl::operator+	(	const RationalFunction< Pol, AS > &	lhs,
		const typename Pol::CoeffType &	rhs
	)

Definition at line 434 of file RationalFunction.h.

operator+() [25/34]

template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>

RationalFunction<Pol, AS> carl::operator+	(	const RationalFunction< Pol, AS > &	lhs,
		Variable	rhs
	)

Definition at line 429 of file RationalFunction.h.

operator+() [26/34]

template<typename C >

auto carl::operator+ ( const Term< C > &  lhs, const C &  rhs  )

inline

Performs an addition involving a polynomial using operator+=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs + rhs

Definition at line 478 of file MultivariatePolynomial_operators.h.

operator+() [27/34]

template<typename C >

auto carl::operator+ ( const Term< C > &  lhs, const Monomial::Arg &  rhs  )

inline

Performs an addition involving a polynomial using operator+=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs + rhs

Definition at line 470 of file MultivariatePolynomial_operators.h.

operator+() [28/34]

template<typename C , typename O , typename P >

auto carl::operator+ ( const Term< C > &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Performs an addition involving a polynomial using operator+=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs + rhs

Definition at line 462 of file MultivariatePolynomial_operators.h.

operator+() [29/34]

template<typename C >

auto carl::operator+ ( const Term< C > &  lhs, const Term< C > &  rhs  )

inline

Performs an addition involving a polynomial using operator+=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs + rhs

Definition at line 466 of file MultivariatePolynomial_operators.h.

operator+() [30/34]

template<typename C >

auto carl::operator+ ( const Term< C > &  lhs, Variable  rhs  )

inline

Performs an addition involving a polynomial using operator+=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs + rhs

Definition at line 474 of file MultivariatePolynomial_operators.h.

operator+() [31/34]

template<typename P >

FactorizedPolynomial<P> carl::operator+ ( const typename FactorizedPolynomial< P >::CoeffType &  _lhs, const FactorizedPolynomial< P > &  _rhs  )

inline

Performs an addition involving a polynomial.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs + _rhs

Definition at line 956 of file FactorizedPolynomial.h.

operator+() [32/34]

template<typename C , EnableIf< carl::is_number_type< C >> = dummy>

auto carl::operator+ ( Variable  lhs, const C &  rhs  )

inline

Performs an addition involving a polynomial using operator+=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs + rhs

Definition at line 502 of file MultivariatePolynomial_operators.h.

operator+() [33/34]

template<typename C , typename O , typename P >

auto carl::operator+ ( Variable  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Performs an addition involving a polynomial using operator+=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs + rhs

Definition at line 494 of file MultivariatePolynomial_operators.h.

operator+() [34/34]

template<typename C >

auto carl::operator+ ( Variable  lhs, const Term< C > &  rhs  )

inline

Performs an addition involving a polynomial using operator+=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs + rhs

Definition at line 498 of file MultivariatePolynomial_operators.h.

operator+=() [1/2]

template<typename Number >

Interval<Number>& carl::operator+= ( Interval< Number > &  lhs, const Interval< Number > &  rhs  )

inline

Operator for the addition of an interval and a number with assignment.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

Resulting interval.

Definition at line 295 of file operators.h.

Here is the call graph for this function:

operator+=() [2/2]

template<typename Number >

Interval<Number>& carl::operator+= ( Interval< Number > &  lhs, const Number &  rhs  )

inline

Operator for the addition of an interval and a number with assignment.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

Resulting interval.

Definition at line 307 of file operators.h.

Here is the call graph for this function:

operator-() [1/37]

BVValue carl::operator- ( const BVValue &  lhs, const BVValue &  rhs  )

inline

Definition at line 166 of file BVValue.h.

Here is the call graph for this function:

operator-() [2/37]

BVValue carl::operator- ( const BVValue &  val )

inline

Definition at line 162 of file BVValue.h.

Here is the call graph for this function:

operator-() [3/37]

template<typename C , EnableIf< carl::is_number_type< C >> = dummy>

auto carl::operator- ( const C &  lhs, const Monomial::Arg &  rhs  )

inline

Performs a subtraction involving a polynomial using operator-=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs - rhs

Definition at line 604 of file MultivariatePolynomial_operators.h.

operator-() [4/37]

template<typename C , typename O , typename P >

auto carl::operator- ( const C &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Performs a subtraction involving a polynomial using operator-=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs - rhs

Definition at line 596 of file MultivariatePolynomial_operators.h.

operator-() [5/37]

template<typename C >

auto carl::operator- ( const C &  lhs, const Term< C > &  rhs  )

inline

Performs a subtraction involving a polynomial using operator-=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs - rhs

Definition at line 600 of file MultivariatePolynomial_operators.h.

operator-() [6/37]

template<typename C , EnableIf< carl::is_number_type< C >> = dummy>

auto carl::operator- ( const C &  lhs, Variable  rhs  )

inline

Performs a subtraction involving a polynomial using operator-=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs - rhs

Definition at line 608 of file MultivariatePolynomial_operators.h.

operator-() [7/37]

template<typename P >

FactorizedPolynomial<P> carl::operator-	(	const FactorizedPolynomial< P > &	_lhs,
		const FactorizedPolynomial< P > &	_rhs
	)

Performs an subtraction involving a polynomial.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs - _rhs

operator-() [8/37]

template<typename P >

FactorizedPolynomial<P> carl::operator-	(	const FactorizedPolynomial< P > &	_lhs,
		const typename FactorizedPolynomial< P >::CoeffType &	_rhs
	)

Performs an subtraction involving a polynomial.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs - _rhs

operator-() [9/37]

template<typename Number >

Interval<Number> carl::operator- ( const Interval< Number > &  lhs, const Interval< Number > &  rhs  )

inline

Operator for the subtraction of two intervals.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

Resulting interval.

Definition at line 329 of file operators.h.

Here is the call graph for this function:

operator-() [10/37]

template<typename Number >

Interval<Number> carl::operator- ( const Interval< Number > &  lhs, const Number &  rhs  )

inline

Operator for the subtraction of an interval and a number.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

Resulting interval.

Definition at line 340 of file operators.h.

Here is the call graph for this function:

operator-() [11/37]

template<typename Number >

Interval<Number> carl::operator- ( const Interval< Number > &  rhs )

inline

Unary minus.

Parameters

rhs	The operand.

Returns

Resulting interval.

Definition at line 318 of file operators.h.

Here is the call graph for this function:

operator-() [12/37]

template<typename C , EnableIf< carl::is_number_type< C >> = dummy>

auto carl::operator- ( const Monomial::Arg &  lhs, const C &  rhs  )

inline

Performs a subtraction involving a polynomial using operator-=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs - rhs

Definition at line 580 of file MultivariatePolynomial_operators.h.

operator-() [13/37]

template<typename C , typename O , typename P >

auto carl::operator- ( const Monomial::Arg &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Performs a subtraction involving a polynomial using operator-=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs - rhs

Definition at line 572 of file MultivariatePolynomial_operators.h.

operator-() [14/37]

template<typename C >

auto carl::operator- ( const Monomial::Arg &  lhs, const Term< C > &  rhs  )

inline

Performs a subtraction involving a polynomial using operator-=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs - rhs

Definition at line 576 of file MultivariatePolynomial_operators.h.

operator-() [15/37]

template<typename C , typename O , typename P >

auto carl::operator- ( const MultivariatePolynomial< C, O, P > &  lhs, const C &  rhs  )

inline

Performs a subtraction involving a polynomial using operator-=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs - rhs

Definition at line 548 of file MultivariatePolynomial_operators.h.

operator-() [16/37]

template<typename C , typename O , typename P >

auto carl::operator- ( const MultivariatePolynomial< C, O, P > &  lhs, const Monomial::Arg &  rhs  )

inline

Performs a subtraction involving a polynomial using operator-=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs - rhs

Definition at line 540 of file MultivariatePolynomial_operators.h.

operator-() [17/37]

template<typename C , typename O , typename P >

auto carl::operator- ( const MultivariatePolynomial< C, O, P > &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Performs a subtraction involving a polynomial using operator-=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs - rhs

Definition at line 532 of file MultivariatePolynomial_operators.h.

operator-() [18/37]

template<typename C , typename O , typename P >

auto carl::operator- ( const MultivariatePolynomial< C, O, P > &  lhs, const Term< C > &  rhs  )

inline

Performs a subtraction involving a polynomial using operator-=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs - rhs

Definition at line 536 of file MultivariatePolynomial_operators.h.

operator-() [19/37]

template<typename C , typename O , typename P >

auto carl::operator- ( const MultivariatePolynomial< C, O, P > &  lhs, Variable  rhs  )

inline

Performs a subtraction involving a polynomial using operator-=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs - rhs

Definition at line 544 of file MultivariatePolynomial_operators.h.

operator-() [20/37]

template<typename Number >

Interval<Number> carl::operator- ( const Number &  lhs, const Interval< Number > &  rhs  )

inline

Operator for the subtraction of an interval and a number.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

Resulting interval.

Definition at line 351 of file operators.h.

operator-() [21/37]

template<typename Pol , bool AS>

RationalFunction<Pol, AS> carl::operator-

(

const RationalFunction< Pol, AS > &

lhs

)

Definition at line 439 of file RationalFunction.h.

operator-() [22/37]

template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>

RationalFunction<Pol, AS> carl::operator-	(	const RationalFunction< Pol, AS > &	lhs,
		const Monomial::Arg &	rhs
	)

Definition at line 459 of file RationalFunction.h.

operator-() [23/37]

template<typename Pol , bool AS>

RationalFunction<Pol, AS> carl::operator-	(	const RationalFunction< Pol, AS > &	lhs,
		const Pol &	rhs
	)

Definition at line 449 of file RationalFunction.h.

operator-() [24/37]

template<typename Pol , bool AS>

RationalFunction<Pol, AS> carl::operator-	(	const RationalFunction< Pol, AS > &	lhs,
		const RationalFunction< Pol, AS > &	rhs
	)

Definition at line 444 of file RationalFunction.h.

operator-() [25/37]

template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>

RationalFunction<Pol, AS> carl::operator-	(	const RationalFunction< Pol, AS > &	lhs,
		const Term< typename Pol::CoeffType > &	rhs
	)

Definition at line 454 of file RationalFunction.h.

operator-() [26/37]

template<typename Pol , bool AS>

RationalFunction<Pol, AS> carl::operator-	(	const RationalFunction< Pol, AS > &	lhs,
		const typename Pol::CoeffType &	rhs
	)

Definition at line 469 of file RationalFunction.h.

operator-() [27/37]

template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>

RationalFunction<Pol, AS> carl::operator-	(	const RationalFunction< Pol, AS > &	lhs,
		Variable	rhs
	)

Definition at line 464 of file RationalFunction.h.

operator-() [28/37]

template<typename C >

auto carl::operator- ( const Term< C > &  lhs, const C &  rhs  )

inline

Performs a subtraction involving a polynomial using operator-=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs - rhs

Definition at line 568 of file MultivariatePolynomial_operators.h.

operator-() [29/37]

template<typename C >

auto carl::operator- ( const Term< C > &  lhs, const Monomial::Arg &  rhs  )

inline

Performs a subtraction involving a polynomial using operator-=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs - rhs

Definition at line 560 of file MultivariatePolynomial_operators.h.

operator-() [30/37]

template<typename C , typename O , typename P >

auto carl::operator- ( const Term< C > &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Performs a subtraction involving a polynomial using operator-=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs - rhs

Definition at line 552 of file MultivariatePolynomial_operators.h.

operator-() [31/37]

template<typename C >

auto carl::operator- ( const Term< C > &  lhs, const Term< C > &  rhs  )

inline

Performs a subtraction involving a polynomial using operator-=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs - rhs

Definition at line 556 of file MultivariatePolynomial_operators.h.

operator-() [32/37]

template<typename C >

auto carl::operator- ( const Term< C > &  lhs, Variable  rhs  )

inline

Performs a subtraction involving a polynomial using operator-=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs - rhs

Definition at line 564 of file MultivariatePolynomial_operators.h.

operator-() [33/37]

template<typename Coeff >

Term<Coeff> carl::operator-

(

const Term< Coeff > &

rhs

)

Definition at line 320 of file Term.h.

Here is the call graph for this function:

operator-() [34/37]

template<typename P >

FactorizedPolynomial<P> carl::operator- ( const typename FactorizedPolynomial< P >::CoeffType &  _lhs, const FactorizedPolynomial< P > &  _rhs  )

inline

Performs an subtraction involving a polynomial.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs - _rhs

Definition at line 977 of file FactorizedPolynomial.h.

operator-() [35/37]

template<typename C , EnableIf< carl::is_number_type< C >> = dummy>

auto carl::operator- ( Variable  lhs, const C &  rhs  )

inline

Performs a subtraction involving a polynomial using operator-=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs - rhs

Definition at line 592 of file MultivariatePolynomial_operators.h.

operator-() [36/37]

template<typename C , typename O , typename P >

auto carl::operator- ( Variable  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Performs a subtraction involving a polynomial using operator-=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs - rhs

Definition at line 584 of file MultivariatePolynomial_operators.h.

operator-() [37/37]

template<typename C >

auto carl::operator- ( Variable  lhs, const Term< C > &  rhs  )

inline

Performs a subtraction involving a polynomial using operator-=().

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs - rhs

Definition at line 588 of file MultivariatePolynomial_operators.h.

operator-=() [1/2]

template<typename Number >

Interval<Number>& carl::operator-= ( Interval< Number > &  lhs, const Interval< Number > &  rhs  )

inline

Operator for the subtraction of two intervals with assignment.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

Resulting interval.

Definition at line 362 of file operators.h.

Here is the call graph for this function:

operator-=() [2/2]

template<typename Number >

Interval<Number>& carl::operator-= ( Interval< Number > &  lhs, const Number &  rhs  )

inline

Operator for the subtraction of an interval and a number with assignment.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

Resulting interval.

Definition at line 374 of file operators.h.

Here is the call graph for this function:

operator/() [1/19]

BVValue carl::operator/ ( const BVValue &  lhs, const BVValue &  rhs  )

inline

Definition at line 175 of file BVValue.h.

Here is the call graph for this function:

operator/() [2/19]

cln::cl_I carl::operator/ ( const cln::cl_I &  a, const cln::cl_I &  b  )

inline

Divide two integers.

Discards the remainder of the division.

Parameters

a	First argument.
b	Second argument.

Returns

.

Definition at line 538 of file operations.h.

Here is the call graph for this function:

operator/() [3/19]

cln::cl_I carl::operator/ ( const cln::cl_I &  lhs, const int &  rhs  )

inline

Definition at line 542 of file operations.h.

operator/() [4/19]

template<typename P >

FactorizedPolynomial<P> carl::operator/ ( const FactorizedPolynomial< P > &  _lhs, const typename FactorizedPolynomial< P >::CoeffType &  _rhs  )

inline

Perform a multiplication involving a polynomial.

Parameters

_lhs	Left hand side.
_rhs	Right hand side.

Returns

_lhs * _rhs

Definition at line 1004 of file FactorizedPolynomial.h.

operator/() [5/19]

template<typename Number >

Interval<Number> carl::operator/ ( const Interval< Number > &  lhs, const Number &  rhs  )

inline

Operator for the division of an interval and a number.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

Resulting interval.

Definition at line 453 of file operators.h.

Here is the call graph for this function:

operator/() [6/19]

template<typename Coeff , EnableIf< carl::is_subset_of_rationals_type< Coeff >> = dummy>

Term<Coeff> carl::operator/ ( const Monomial::Arg &  lhs, const Coeff &  rhs  )

inline

Perform a multiplication involving a term.

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 598 of file Term.h.

Here is the call graph for this function:

operator/() [7/19]

mpq_class carl::operator/ ( const mpq_class &  n, const mpq_class &  d  )

inline

Definition at line 464 of file operations.h.

Here is the call graph for this function:

operator/() [8/19]

mpz_class carl::operator/ ( const mpz_class &  n, const mpz_class &  d  )

inline

Definition at line 452 of file operations.h.

Here is the call graph for this function:

operator/() [9/19]

template<typename C , typename O , typename P , EnableIf< carl::is_number_type< C >> = dummy>

MultivariatePolynomial<C,O,P> carl::operator/ ( const MultivariatePolynomial< C, O, P > &  lhs, const C &  rhs  )

inline

Perform a division involving a polynomial.

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs / rhs

Definition at line 612 of file MultivariatePolynomial.h.

operator/() [10/19]

template<typename C , typename O , typename P >

MultivariatePolynomial<C,O,P> carl::operator/	(	const MultivariatePolynomial< C, O, P > &	lhs,
		const MultivariatePolynomial< C, O, P > &	rhs
	)

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs / rhs

Definition at line 242 of file Division.h.

operator/() [11/19]

template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>

RationalFunction<Pol, AS> carl::operator/	(	const RationalFunction< Pol, AS > &	lhs,
		const Monomial::Arg &	rhs
	)

Definition at line 534 of file RationalFunction.h.

operator/() [12/19]

template<typename Pol , bool AS>

RationalFunction<Pol, AS> carl::operator/	(	const RationalFunction< Pol, AS > &	lhs,
		const Pol &	rhs
	)

Definition at line 524 of file RationalFunction.h.

operator/() [13/19]

template<typename Pol , bool AS>

RationalFunction<Pol, AS> carl::operator/	(	const RationalFunction< Pol, AS > &	lhs,
		const RationalFunction< Pol, AS > &	rhs
	)

Definition at line 519 of file RationalFunction.h.

operator/() [14/19]

template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>

RationalFunction<Pol, AS> carl::operator/	(	const RationalFunction< Pol, AS > &	lhs,
		const Term< typename Pol::CoeffType > &	rhs
	)

Definition at line 529 of file RationalFunction.h.

operator/() [15/19]

template<typename Pol , bool AS>

RationalFunction<Pol, AS> carl::operator/	(	const RationalFunction< Pol, AS > &	lhs,
		const typename Pol::CoeffType &	rhs
	)

Definition at line 544 of file RationalFunction.h.

operator/() [16/19]

template<typename Pol , bool AS>

RationalFunction<Pol, AS> carl::operator/	(	const RationalFunction< Pol, AS > &	lhs,
		unsigned long	rhs
	)

Definition at line 549 of file RationalFunction.h.

operator/() [17/19]

template<typename Pol , bool AS, DisableIf< needs_cache_type< Pol >> = dummy>

RationalFunction<Pol, AS> carl::operator/	(	const RationalFunction< Pol, AS > &	lhs,
		Variable	rhs
	)

Definition at line 539 of file RationalFunction.h.

operator/() [18/19]

template<typename Coeff , EnableIf< carl::is_subset_of_rationals_type< Coeff >> = dummy>

Term<Coeff> carl::operator/ ( const Term< Coeff > &  lhs, const Coeff &  rhs  )

inline

Perform a multiplication involving a term.

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 594 of file Term.h.

Here is the call graph for this function:

operator/() [19/19]

template<typename Coeff , EnableIf< carl::is_subset_of_rationals_type< Coeff >> = dummy>

Term<Coeff> carl::operator/ ( Variable &  lhs, const Coeff &  rhs  )

inline

Perform a multiplication involving a term.

Parameters

lhs	Left hand side.
rhs	Right hand side.

Returns

lhs * rhs

Definition at line 602 of file Term.h.

Here is the call graph for this function:

operator/=()

template<typename Number >

Interval<Number>& carl::operator/= ( Interval< Number > &  lhs, const Number &  rhs  )

inline

Operator for the division of an interval and a number with assignment.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

Resulting interval.

Definition at line 469 of file operators.h.

operator<() [1/62]

template<typename P >

bool carl::operator<	(	const BasicConstraint< P > &	lhs,
		const BasicConstraint< P > &	rhs
	)

Definition at line 117 of file BasicConstraint.h.

Here is the call graph for this function:

operator<() [2/62]

bool carl::operator<	(	const BVConstraint &	lhs,
		const BVConstraint &	rhs
	)

Definition at line 25 of file BVConstraint.cpp.

Here is the call graph for this function:

operator<() [3/62]

bool carl::operator<	(	const BVTerm &	lhs,
		const BVTerm &	rhs
	)

Definition at line 133 of file BVTerm.cpp.

operator<() [4/62]

bool carl::operator< ( const BVTermContent &  lhs, const BVTermContent &  rhs  )

inline

Definition at line 213 of file BVTermContent.h.

Here is the call graph for this function:

operator<() [5/62]

bool carl::operator< ( const BVValue &  lhs, const BVValue &  rhs  )

inline

Definition at line 151 of file BVValue.h.

Here is the call graph for this function:

operator<() [6/62]

bool carl::operator< ( const BVVariable &  lhs, const BVVariable &  rhs  )

inline

Definition at line 79 of file BVVariable.h.

Here is the call graph for this function:

operator<() [7/62]

bool carl::operator< ( const BVVariable &  lhs, const Variable &  rhs  )

inline

Definition at line 82 of file BVVariable.h.

Here is the call graph for this function:

operator<() [8/62]

template<typename C , typename O , typename P >

bool carl::operator< ( const C &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first arguments is less than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs < rhs

Definition at line 237 of file MultivariatePolynomial_operators.h.

Here is the call graph for this function:

operator<() [9/62]

template<typename Coeff >

bool carl::operator<	(	const Coeff &	lhs,
		const Term< Coeff > &	rhs
	)

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

operator<() [10/62]

template<typename P >

bool carl::operator<	(	const Constraint< P > &	lhs,
		const Constraint< P > &	rhs
	)

Definition at line 298 of file Constraint.h.

operator<() [11/62]

template<typename Coeff , typename Ordering , typename Policies >

bool carl::operator<	(	const ContextPolynomial< Coeff, Ordering, Policies > &	lhs,
		const ContextPolynomial< Coeff, Ordering, Policies > &	rhs
	)

Definition at line 140 of file ContextPolynomial.h.

Here is the call graph for this function:

operator<() [12/62]

template<typename P >

bool carl::operator<	(	const FactorizedPolynomial< P > &	_lhs,
		const FactorizedPolynomial< P > &	_rhs
	)

Checks if the first arguments is less than the second.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs < _rhs

operator<() [13/62]

template<typename P >

bool carl::operator<	(	const FactorizedPolynomial< P > &	_lhs,
		const typename FactorizedPolynomial< P >::CoeffType &	_rhs
	)

Checks if the first arguments is less than the second.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs < _rhs

operator<() [14/62]

template<typename Number >

bool carl::operator< ( const Interval< Number > &  lhs, const Interval< Number > &  rhs  )

inline

Operator for the comparison of two intervals.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

True if the lefthand side is smaller than the righthand side.

Definition at line 138 of file operators.h.

Here is the call graph for this function:

operator<() [15/62]

template<typename Number >

bool carl::operator< ( const Interval< Number > &  lhs, const Number &  rhs  )

inline

Definition at line 153 of file operators.h.

Here is the call graph for this function:

operator<() [16/62]

template<typename Number >

bool carl::operator< ( const LowerBound< Number > &  lhs, const LowerBound< Number > &  rhs  )

inline

Operators for LowerBound and UpperBound.

Definition at line 11 of file operators.h.

operator<() [17/62]

template<typename Rational , typename Poly >

bool carl::operator<	(	const ModelValue< Rational, Poly > &	lhs,
		const ModelValue< Rational, Poly > &	rhs
	)

Definition at line 300 of file ModelValue.h.

operator<() [18/62]

bool carl::operator< ( const ModelVariable &  lhs, const ModelVariable &  rhs  )

inline

Return true if lhs is smaller than rhs.

Definition at line 112 of file ModelVariable.h.

operator<() [19/62]

bool carl::operator< ( const Monomial::Arg &  lhs, const Monomial::Arg &  rhs  )

inline

Compares two arguments where one is a Monomial and the other is either a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 534 of file Monomial.h.

Here is the call graph for this function:

operator<() [20/62]

template<typename C , typename O , typename P >

bool carl::operator< ( const Monomial::Arg &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first arguments is less than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs < rhs

Definition at line 223 of file MultivariatePolynomial_operators.h.

Here is the call graph for this function:

operator<() [21/62]

template<typename Coeff >

bool carl::operator<	(	const Monomial::Arg &	lhs,
		const Term< Coeff > &	rhs
	)

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

operator<() [22/62]

bool carl::operator< ( const Monomial::Arg &  lhs, Variable  rhs  )

inline

Compares two arguments where one is a Monomial and the other is either a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 549 of file Monomial.h.

operator<() [23/62]

template<typename C , typename O , typename P >

bool carl::operator< ( const MultivariatePolynomial< C, O, P > &  lhs, const C &  rhs  )

inline

Checks if the first arguments is less than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs < rhs

Definition at line 211 of file MultivariatePolynomial_operators.h.

Here is the call graph for this function:

operator<() [24/62]

template<typename C , typename O , typename P >

bool carl::operator< ( const MultivariatePolynomial< C, O, P > &  lhs, const Monomial::Arg &  rhs  )

inline

Checks if the first arguments is less than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs < rhs

Definition at line 201 of file MultivariatePolynomial_operators.h.

Here is the call graph for this function:

operator<() [25/62]

template<typename C , typename O , typename P >

bool carl::operator< ( const MultivariatePolynomial< C, O, P > &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first arguments is less than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs < rhs

Definition at line 175 of file MultivariatePolynomial_operators.h.

Here is the call graph for this function:

operator<() [26/62]

template<typename C , typename O , typename P >

bool carl::operator< ( const MultivariatePolynomial< C, O, P > &  lhs, const Term< C > &  rhs  )

inline

Checks if the first arguments is less than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs < rhs

Definition at line 196 of file MultivariatePolynomial_operators.h.

Here is the call graph for this function:

operator<() [27/62]

template<typename C , typename O , typename P >

bool carl::operator< ( const MultivariatePolynomial< C, O, P > &  lhs, Variable  rhs  )

inline

Checks if the first arguments is less than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs < rhs

Definition at line 206 of file MultivariatePolynomial_operators.h.

Here is the call graph for this function:

operator<() [28/62]

template<typename Poly >

bool carl::operator< ( const MultivariateRoot< Poly > &  lhs, const MultivariateRoot< Poly > &  rhs  )

inline

Definition at line 99 of file MultivariateRoot.h.

Here is the call graph for this function:

operator<() [29/62]

template<typename N >

bool carl::operator<	(	const N &	lhs,
		const ThomEncoding< N > &	rhs
	)

Definition at line 586 of file ThomEncoding.h.

operator<() [30/62]

template<typename Number >

bool carl::operator< ( const Number &  lhs, const Interval< Number > &  rhs  )

inline

Definition at line 167 of file operators.h.

Here is the call graph for this function:

operator<() [31/62]

template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>

bool carl::operator<	(	const Number &	lhs,
		const RAN &	rhs
	)

Definition at line 67 of file Operations.h.

operator<() [32/62]

template<typename Number >

bool carl::operator<	(	const Number &	lhs,
		const RealAlgebraicNumberThom< Number > &	rhs
	)

Definition at line 206 of file ran_thom.h.

operator<() [33/62]

template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>

bool carl::operator<	(	const RAN &	lhs,
		const Number &	rhs
	)

Definition at line 42 of file Operations.h.

Here is the call graph for this function:

operator<() [34/62]

template<typename RAN , EnableIf< is_ran_type< RAN >> = dummy>

bool carl::operator<	(	const RAN &	lhs,
		const RAN &	rhs
	)

Definition at line 92 of file Operations.h.

Here is the call graph for this function:

operator<() [35/62]

template<typename Number >

bool carl::operator<	(	const RealAlgebraicNumberThom< Number > &	lhs,
		const Number &	rhs
	)

Definition at line 201 of file ran_thom.h.

operator<() [36/62]

template<typename Number >

bool carl::operator<	(	const RealAlgebraicNumberThom< Number > &	lhs,
		const RealAlgebraicNumberThom< Number > &	rhs
	)

Definition at line 195 of file ran_thom.h.

operator<() [37/62]

bool carl::operator< ( const SortContent &  lhs, const SortContent &  rhs  )

inline

Parameters

lhs	Left SortContent
rhs	Right SortContent

Returns

lhs < rhs

Definition at line 86 of file SortManager.h.

operator<() [38/62]

bool carl::operator< ( const SortValue &  lhs, const SortValue &  rhs  )

inline

Orders two sort values.

Definition at line 82 of file SortValue.h.

Here is the call graph for this function:

operator<() [39/62]

template<typename C , typename O , typename P >

bool carl::operator< ( const Term< C > &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first arguments is less than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs < rhs

Definition at line 216 of file MultivariatePolynomial_operators.h.

Here is the call graph for this function:

operator<() [40/62]

template<typename Coeff >

bool carl::operator<	(	const Term< Coeff > &	lhs,
		const Coeff &	rhs
	)

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

operator<() [41/62]

template<typename Coeff >

bool carl::operator<	(	const Term< Coeff > &	lhs,
		const Monomial::Arg &	rhs
	)

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

operator<() [42/62]

template<typename Coeff >

bool carl::operator<	(	const Term< Coeff > &	lhs,
		const Term< Coeff > &	rhs
	)

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

operator<() [43/62]

template<typename Coeff >

bool carl::operator<	(	const Term< Coeff > &	lhs,
		Variable	rhs
	)

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

operator<() [44/62]

template<typename N >

bool carl::operator<	(	const ThomEncoding< N > &	lhs,
		const N &	rhs
	)

Definition at line 573 of file ThomEncoding.h.

operator<() [45/62]

template<typename N >

bool carl::operator<	(	const ThomEncoding< N > &	lhs,
		const ThomEncoding< N > &	rhs
	)

Definition at line 559 of file ThomEncoding.h.

operator<() [46/62]

template<typename P >

bool carl::operator< ( const typename FactorizedPolynomial< P >::CoeffType &  _lhs, const FactorizedPolynomial< P > &  _rhs  )

inline

Checks if the first arguments is less than the second.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs < _rhs

Definition at line 854 of file FactorizedPolynomial.h.

operator<() [47/62]

bool carl::operator< ( const UEquality &  lhs, const UEquality &  rhs  )

inline

Parameters

lhs	The left hand side.
rhs	The right hand side.

Returns

true, if the left equality is less than the right one.

Definition at line 132 of file UEquality.h.

Here is the call graph for this function:

operator<() [48/62]

bool carl::operator< ( const UFContent &  lhs, const UFContent &  rhs  )

inline

Parameters

lhs	Left UFContent.
rhs	Right UFContent.

Returns

true, if lhs is smaller than rhs.

Definition at line 90 of file UFManager.h.

Here is the call graph for this function:

operator<() [49/62]

bool carl::operator< ( const UFInstance &  lhs, const UFInstance &  rhs  )

inline

Parameters

lhs	The left function instance.
rhs	The right function instance.

Returns

true, if lhs < rhs.

Definition at line 81 of file UFInstance.h.

Here is the call graph for this function:

operator<() [50/62]

bool carl::operator< ( const UFModel &  lhs, const UFModel &  rhs  )

inline

Checks whether one UFModel is smaller than another.

Returns

true, if one uninterpreted function model is less than the other.

Definition at line 58 of file UFModel.h.

Here is the call graph for this function:

operator<() [51/62]

bool carl::operator< ( const UninterpretedFunction &  lhs, const UninterpretedFunction &  rhs  )

inline

Check whether one uninterpreted function is smaller than another.

Returns

true, if one uninterpreted function is less than the other one.

Definition at line 81 of file UninterpretedFunction.h.

Here is the call graph for this function:

operator<() [52/62]

template<typename Number >

bool carl::operator< ( const UpperBound< Number > &  lhs, const LowerBound< Number > &  rhs  )

inline

Definition at line 33 of file operators.h.

operator<() [53/62]

template<typename Number >

bool carl::operator< ( const UpperBound< Number > &  lhs, const UpperBound< Number > &  rhs  )

inline

Definition at line 48 of file operators.h.

operator<() [54/62]

bool carl::operator<	(	const UTerm &	lhs,
		const UTerm &	rhs
	)

Parameters

lhs	The uninterpreted term to the left.
rhs	The uninterpreted term to the right.

Returns

true, if lhs is smaller than rhs.

Definition at line 56 of file UTerm.cpp.

Here is the call graph for this function:

operator<() [55/62]

bool carl::operator< ( const Variable &  lhs, const BVVariable &  rhs  )

inline

Definition at line 85 of file BVVariable.h.

Here is the call graph for this function:

operator<() [56/62]

template<typename Poly >

bool carl::operator<	(	const VariableAssignment< Poly > &	lhs,
		const VariableAssignment< Poly > &	rhs
	)

Definition at line 56 of file VariableAssignment.h.

operator<() [57/62]

template<typename Poly >

bool carl::operator<	(	const VariableComparison< Poly > &	lhs,
		const VariableComparison< Poly > &	rhs
	)

Definition at line 198 of file VariableComparison.h.

Here is the call graph for this function:

operator<() [58/62]

bool carl::operator< ( Sort  lhs, Sort  rhs  )

inline

Checks whether one sort is smaller than another.

Returns

true, if lhs is less than rhs.

Definition at line 86 of file Sort.h.

Here is the call graph for this function:

operator<() [59/62]

bool carl::operator< ( UVariable  lhs, UVariable  rhs  )

inline

Parameters

lhs	The left variable.
rhs	The right variable.

Returns

true, if the left variable is smaller.

Definition at line 92 of file UVariable.h.

Here is the call graph for this function:

operator<() [60/62]

bool carl::operator< ( Variable  lhs, const Monomial::Arg &  rhs  )

inline

Compares two arguments where one is a Monomial and the other is either a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 555 of file Monomial.h.

operator<() [61/62]

template<typename C , typename O , typename P >

bool carl::operator< ( Variable  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first arguments is less than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs < rhs

Definition at line 230 of file MultivariatePolynomial_operators.h.

Here is the call graph for this function:

operator<() [62/62]

template<typename Coeff >

bool carl::operator<	(	Variable	lhs,
		const Term< Coeff > &	rhs
	)

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

operator<<() [1/77]

BVValue carl::operator<< ( const BVValue &  lhs, const BVValue &  rhs  )

inline

Definition at line 194 of file BVValue.h.

Here is the call graph for this function:

operator<<() [2/77]

std::ostream& carl::operator<< ( std::ostream &  _os, const BVCompareRelation &  _r  )

inline

Definition at line 47 of file BVCompareRelation.h.

Here is the call graph for this function:

operator<<() [3/77]

std::ostream& carl::operator<<	(	std::ostream &	_os,
		const Sort &	_sort
	)

Parameters

_os	The output stream to print on.
_sort	The sort to print.

Returns

The output stream after printing the given sort on it.

Definition at line 18 of file Sort.cpp.

operator<<() [4/77]

template<typename P >

std::ostream& carl::operator<<	(	std::ostream &	_out,
		const Factorization< P > &	_factorization
	)

operator<<() [5/77]

template<typename P >

std::ostream& carl::operator<<	(	std::ostream &	_out,
		const FactorizedPolynomial< P > &	_fpoly
	)

Prints the factorization representation of the given factorized polynomial on the given output stream.

Parameters

_out	The stream to print on.
_fpoly	The factorized polynomial to print.

Returns

The output stream after inserting the output.

operator<<() [6/77]

template<typename C >

std::ostream& carl::operator<<	(	std::ostream &	o,
		const MultiplicationTable< C > &	table
	)

Definition at line 299 of file MultiplicationTable.h.

operator<<() [7/77]

std::ostream& carl::operator<< ( std::ostream &  os, BoundType  b  )

inline

Definition at line 22 of file BoundType.h.

operator<<() [8/77]

std::ostream& carl::operator<< ( std::ostream &  os, BVTermType  type  )

inline

Definition at line 29 of file BVTermType.h.

Here is the call graph for this function:

operator<<() [9/77]

std::ostream & carl::operator<<	(	std::ostream &	os,
		CMakeOptionPrinter	cmop
	)

Definition at line 12 of file CompileInfo.cpp.

Here is the call graph for this function:

operator<<() [10/77]

std::ostream& carl::operator<< ( std::ostream &  os, CompareResult  cr  )

inline

Definition at line 14 of file CompareResult.h.

operator<<() [11/77]

template<typename Poly >

std::ostream& carl::operator<<	(	std::ostream &	os,
		const BasicConstraint< Poly > &	c
	)

Prints the given constraint on the given stream.

Parameters

os	The stream to print the given constraint on.
c	The formula to print.

Returns

The stream after printing the given constraint on it.

Definition at line 150 of file BasicConstraint.h.

Here is the call graph for this function:

Here is the caller graph for this function:

operator<<() [12/77]

std::ostream& carl::operator<< ( std::ostream &  os, const BitVector &  bv  )

inline

Definition at line 194 of file BitVector.h.

Here is the call graph for this function:

operator<<() [13/77]

template<class Key , class T , class Compare , class AllocatorOrContainer >

std::ostream& carl::operator<< ( std::ostream &  os, const boost::container::flat_map< Key, T, Compare, AllocatorOrContainer > &  m  )

inline

Output a boost::container::flat_map with arbitrary content.

The format is {<key>:<value>, <key>:<value>, ...}

Parameters

os	Output stream.
m	map to be printed.

Returns

Output stream.

Definition at line 237 of file streamingOperators.h.

Here is the call graph for this function:

operator<<() [14/77]

template<typename T , typename C >

std::ostream& carl::operator<< ( std::ostream &  os, const boost::container::flat_set< T, C > &  s  )

inline

Output a boost::container::flat_set with arbitrary content.

The format is {<length>: <item>, <item>, ...}

Parameters

os	Output stream.
s	set to be printed.

Returns

Output stream.

Definition at line 186 of file streamingOperators.h.

Here is the call graph for this function:

operator<<() [15/77]

std::ostream & carl::operator<<	(	std::ostream &	os,
		const BVConstraint &	c
	)

Definition at line 32 of file BVConstraint.cpp.

Here is the call graph for this function:

operator<<() [16/77]

std::ostream & carl::operator<<	(	std::ostream &	os,
		const BVTerm &	term
	)

Definition at line 137 of file BVTerm.cpp.

operator<<() [17/77]

std::ostream& carl::operator<< ( std::ostream &  os, const BVTermContent &  term  )

inline

The output operator of a term.

Parameters

os	Output stream.
term	Content of a bitvector term.

Definition at line 223 of file BVTermContent.h.

Here is the call graph for this function:

operator<<() [18/77]

std::ostream& carl::operator<< ( std::ostream &  os, const BVValue &  val  )

inline

Definition at line 202 of file BVValue.h.

operator<<() [19/77]

std::ostream& carl::operator<< ( std::ostream &  os, const carlVariables &  vars  )

inline

Definition at line 213 of file Variables.h.

operator<<() [20/77]

template<typename Poly >

std::ostream& carl::operator<<	(	std::ostream &	os,
		const Constraint< Poly > &	c
	)

Prints the given constraint on the given stream.

Parameters

os	The stream to print the given constraint on.
c	The formula to print.

Returns

The stream after printing the given constraint on it.

Definition at line 324 of file Constraint.h.

operator<<() [21/77]

std::ostream& carl::operator<< ( std::ostream &  os, const Context &  ctx  )

inline

Definition at line 39 of file Context.h.

Here is the call graph for this function:

operator<<() [22/77]

template<typename Coeff , typename Ordering , typename Policies >

std::ostream& carl::operator<<	(	std::ostream &	os,
		const ContextPolynomial< Coeff, Ordering, Policies > &	rhs
	)

Definition at line 150 of file ContextPolynomial.h.

Here is the call graph for this function:

operator<<() [23/77]

template<typename P >

std::ostream& carl::operator<< ( std::ostream &  os, const Formula< P > &  f  )

inline

The output operator of a formula.

Parameters

os	The stream to print on.
f	The formula to print.

Definition at line 776 of file Formula.h.

operator<<() [24/77]

template<typename Pol >

std::ostream& carl::operator<<	(	std::ostream &	os,
		const FormulaContent< Pol > &	f
	)

The output operator of a formula.

Parameters

os	The stream to print on.
f

Definition at line 273 of file FormulaContent.h.

Here is the call graph for this function:

operator<<() [25/77]

template<typename Pol >

std::ostream& carl::operator<<	(	std::ostream &	os,
		const FormulaContent< Pol > *	fc
	)

Definition at line 308 of file FormulaContent.h.

operator<<() [26/77]

std::ostream& carl::operator<< ( std::ostream &  os, const InfinityValue &  iv  )

inline

Definition at line 44 of file ModelValue.h.

operator<<() [27/77]

template<typename Num >

std::ostream& carl::operator<<	(	std::ostream &	os,
		const IntRepRealAlgebraicNumber< Num > &	ran
	)

Definition at line 475 of file Ran.h.

Here is the call graph for this function:

operator<<() [28/77]

std::ostream& carl::operator<< ( std::ostream &  os, const Logic &  l  )

inline

Definition at line 11 of file Logic.h.

operator<<() [29/77]

template<typename Number >

std::ostream& carl::operator<<	(	std::ostream &	os,
		const LowerBound< Number > &	lb
	)

Definition at line 101 of file Interval.h.

operator<<() [30/77]

template<typename Rational , typename Poly >

std::ostream& carl::operator<<	(	std::ostream &	os,
		const Model< Rational, Poly > &	model
	)

Definition at line 202 of file Model.h.

Here is the call graph for this function:

operator<<() [31/77]

template<typename Rational , typename Poly >

std::ostream& carl::operator<< ( std::ostream &  os, const ModelSubstitution< Rational, Poly > &  ms  )

inline

Definition at line 77 of file ModelSubstitution.h.

Here is the call graph for this function:

operator<<() [32/77]

template<typename Rational , typename Poly >

std::ostream& carl::operator<< ( std::ostream &  os, const ModelSubstitutionPtr< Rational, Poly > &  ms  )

inline

Definition at line 82 of file ModelSubstitution.h.

operator<<() [33/77]

template<typename R , typename P >

std::ostream& carl::operator<< ( std::ostream &  os, const ModelValue< R, P > &  mv  )

inline

Definition at line 305 of file ModelValue.h.

operator<<() [34/77]

std::ostream& carl::operator<< ( std::ostream &  os, const ModelVariable &  mv  )

inline

Definition at line 116 of file ModelVariable.h.

operator<<() [35/77]

std::ostream& carl::operator<< ( std::ostream &  os, const Monomial &  rhs  )

inline

Streaming operator for Monomial.

Parameters

os	Output stream.
rhs	Monomial.

Returns

os

Definition at line 623 of file Monomial.h.

Here is the call graph for this function:

operator<<() [36/77]

std::ostream& carl::operator<< ( std::ostream &  os, const Monomial::Arg &  rhs  )

inline

Streaming operator for std::shared_ptr<Monomial>.

Parameters

os	Output stream.
rhs	Monomial.

Returns

os

Definition at line 640 of file Monomial.h.

operator<<() [37/77]

std::ostream& carl::operator<< ( std::ostream &  os, const MonomialPool &  mp  )

inline

Definition at line 159 of file MonomialPool.h.

operator<<() [38/77]

template<typename C , typename O , typename P >

std::ostream& carl::operator<< ( std::ostream &  os, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Streaming operator for multivariate polynomials.

Parameters

os	Output stream.
rhs	Polynomial.

Returns

os.

Definition at line 630 of file MultivariatePolynomial.h.

Here is the call graph for this function:

operator<<() [39/77]

template<typename P >

std::ostream& carl::operator<<	(	std::ostream &	os,
		const MultivariateRoot< P > &	mr
	)

Definition at line 104 of file MultivariateRoot.h.

Here is the call graph for this function:

operator<<() [40/77]

std::ostream& carl::operator<< ( std::ostream &  os, const Quantifier &  type  )

inline

Definition at line 14 of file PNF.h.

operator<<() [41/77]

template<typename Num >

std::ostream& carl::operator<<	(	std::ostream &	os,
		const RealAlgebraicNumberThom< Num > &	rhs
	)

Definition at line 211 of file ran_thom.h.

operator<<() [42/77]

template<class C >

std::ostream& carl::operator<<	(	std::ostream &	os,
		const ReductorEntry< C >	rhs
	)

Definition at line 150 of file ReductorEntry.h.

operator<<() [43/77]

std::ostream& carl::operator<< ( std::ostream &  os, const Relation &  r  )

inline

Definition at line 22 of file Relation.h.

operator<<() [44/77]

std::ostream& carl::operator<< ( std::ostream &  os, const Sign &  sign  )

inline

Definition at line 29 of file Sign.h.

operator<<() [45/77]

template<typename N >

std::ostream& carl::operator<<	(	std::ostream &	os,
		const SignDetermination< N > &	rhs
	)

Definition at line 412 of file SignDetermination.h.

Here is the call graph for this function:

operator<<() [46/77]

std::ostream& carl::operator<< ( std::ostream &  os, const SortValue &  sv  )

inline

Prints the given sort value on the given output stream.

Parameters

os	The output stream to print on.
sv	The sort value to print.

Returns

The output stream after printing the given sort value on it.

Definition at line 67 of file SortValue.h.

Here is the call graph for this function:

operator<<() [47/77]

template<typename T >

std::ostream & carl::operator<< ( std::ostream &  os, const std::deque< T > &  v  )

inline

Output a std::deque with arbitrary content.

The format is [<length>: <item>, <item>, ...]

Parameters

os	Output stream.
v	vector to be printed.

Returns

Output stream.

Definition at line 285 of file streamingOperators.h.

Here is the call graph for this function:

operator<<() [48/77]

template<typename T >

std::ostream & carl::operator<< ( std::ostream &  os, const std::forward_list< T > &  l  )

inline

Output a std::forward_list with arbitrary content.

The format is [<item>, <item>, ...]

Parameters

os	Output stream.
l	list to be printed.

Returns

Output stream.

Definition at line 89 of file streamingOperators.h.

Here is the call graph for this function:

operator<<() [49/77]

template<typename T >

std::ostream & carl::operator<< ( std::ostream &  os, const std::initializer_list< T > &  l  )

inline

Output a std::initializer_list with arbitrary content.

The format is [<item>, <item>, ...]

Parameters

os	Output stream.
l	list to be printed.

Returns

Output stream.

Definition at line 101 of file streamingOperators.h.

Here is the call graph for this function:

operator<<() [50/77]

template<typename T >

std::ostream & carl::operator<< ( std::ostream &  os, const std::list< T > &  l  )

inline

Output a std::list with arbitrary content.

The format is [<length>: <item>, <item>, ...]

Parameters

os	Output stream.
l	list to be printed.

Returns

Output stream.

Definition at line 113 of file streamingOperators.h.

Here is the call graph for this function:

operator<<() [51/77]

template<typename Key , typename Value , typename Comparator >

std::ostream & carl::operator<< ( std::ostream &  os, const std::map< Key, Value, Comparator > &  m  )

inline

Output a std::map with arbitrary content.

The format is {<key>:<value>, <key>:<value>, ...}

Parameters

os	Output stream.
m	map to be printed.

Returns

Output stream.

Definition at line 125 of file streamingOperators.h.

Here is the call graph for this function:

operator<<() [52/77]

template<typename Key , typename Value , typename Comparator >

std::ostream & carl::operator<< ( std::ostream &  os, const std::multimap< Key, Value, Comparator > &  m  )

inline

Output a std::multimap with arbitrary content.

The format is {<key>:<value>, <key>:<value>, ...}

Parameters

os	Output stream.
m	multimap to be printed.

Returns

Output stream.

Definition at line 137 of file streamingOperators.h.

Here is the call graph for this function:

operator<<() [53/77]

template<typename T >

std::ostream & carl::operator<< ( std::ostream &  os, const std::optional< T > &  o  )

inline

Output a std::optional with arbitrary content.

Prints empty if the optional holds no value and forwards the call to the content otherwise.

Parameters

os	Output stream.
o	optional to be printed.

Returns

Output stream.

Definition at line 149 of file streamingOperators.h.

operator<<() [54/77]

template<typename U , typename V >

std::ostream & carl::operator<< ( std::ostream &  os, const std::pair< U, V > &  p  )

inline

Output a std::pair with arbitrary content.

The format is (<first>, <second>)

Parameters

os	Output stream.
p	pair to be printed.

Returns

Output stream.

Definition at line 162 of file streamingOperators.h.

operator<<() [55/77]

template<typename T , typename C >

std::ostream & carl::operator<< ( std::ostream &  os, const std::set< T, C > &  s  )

inline

Output a std::set with arbitrary content.

The format is {<length>: <item>, <item>, ...}

Parameters

os	Output stream.
s	set to be printed.

Returns

Output stream.

Definition at line 174 of file streamingOperators.h.

Here is the call graph for this function:

operator<<() [56/77]

template<typename... T>

std::ostream & carl::operator<<	(	std::ostream &	os,
		const std::tuple< T... > &	t
	)

Output a std::tuple with arbitrary content.

The format is (<item>, <item>, ...)

Parameters

os	Output stream.
t	tuple to be printed.

Returns

Output stream.

Definition at line 213 of file streamingOperators.h.

Here is the call graph for this function:

operator<<() [57/77]

template<typename Key , typename Value , typename H , typename E , typename A >

std::ostream & carl::operator<< ( std::ostream &  os, const std::unordered_map< Key, Value, H, E, A > &  m  )

inline

Output a std::unordered_map with arbitrary content.

The format is {<key>:<value>, <key>:<value>, ...}

Parameters

os	Output stream.
m	map to be printed.

Returns

Output stream.

Definition at line 225 of file streamingOperators.h.

Here is the call graph for this function:

operator<<() [58/77]

template<typename T , typename H , typename K , typename A >

std::ostream & carl::operator<< ( std::ostream &  os, const std::unordered_set< T, H, K, A > &  s  )

inline

Output a std::unordered_set with arbitrary content.

The format is {<length>: <item>, <item>, ...}

Parameters

os	Output stream.
s	unordered_set to be printed.

Returns

Output stream.

Definition at line 249 of file streamingOperators.h.

Here is the call graph for this function:

operator<<() [59/77]

template<typename T , typename... Tail>

std::ostream & carl::operator<< ( std::ostream &  os, const std::variant< T, Tail... > &  v  )

inline

Output a std::variant with arbitrary content.

The call is simply forwarded to whatever content is currently stored in the variant.

Parameters

os	Output stream.
v	variant to be printed.

Returns

Output stream.

Definition at line 261 of file streamingOperators.h.

Here is the call graph for this function:

operator<<() [60/77]

template<typename T >

std::ostream & carl::operator<< ( std::ostream &  os, const std::vector< T > &  v  )

inline

Output a std::vector with arbitrary content.

The format is [<length>: <item>, <item>, ...]

Parameters

os	Output stream.
v	vector to be printed.

Returns

Output stream.

Definition at line 273 of file streamingOperators.h.

Here is the call graph for this function:

operator<<() [61/77]

template<typename N >

std::ostream& carl::operator<<	(	std::ostream &	os,
		const ThomEncoding< N > &	rhs
	)

Definition at line 602 of file ThomEncoding.h.

operator<<() [62/77]

std::ostream& carl::operator<< ( std::ostream &  os, const Timer &  t  )

inline

Streaming operator for a Timer.

Prints the result of t.passed().

Parameters

os	Output stream.
t	Timer.

Returns

os.

Definition at line 51 of file Timer.h.

Here is the call graph for this function:

operator<<() [63/77]

template<typename TT >

std::ostream& carl::operator<<	(	std::ostream &	os,
		const tree< TT > &	tree
	)

Definition at line 986 of file carlTree.h.

Here is the call graph for this function:

operator<<() [64/77]

std::ostream& carl::operator<< ( std::ostream &  os, const UEquality &  ueq  )

inline

Prints the given uninterpreted equality on the given output stream.

Parameters

os	The output stream to print on.
ueq	The uninterpreted equality to print.

Returns

The output stream after printing the given uninterpreted equality on it.

Definition at line 142 of file UEquality.h.

Here is the call graph for this function:

operator<<() [65/77]

std::ostream & carl::operator<<	(	std::ostream &	os,
		const UFInstance &	ufun
	)

Prints the given uninterpreted function instance on the given output stream.

Parameters

os	The output stream to print on.
ufun	The uninterpreted function instance to print.

Returns

The output stream after printing the given uninterpreted function instance on it.

Definition at line 51 of file UFInstance.cpp.

Here is the call graph for this function:

operator<<() [66/77]

std::ostream & carl::operator<<	(	std::ostream &	os,
		const UFModel &	ufm
	)

Prints the given uninterpreted function model on the given output stream.

Parameters

os	The output stream to print on.
ufm	The uninterpreted function model to print.

Returns

The output stream after printing the given uninterpreted function model on it.

Definition at line 29 of file UFModel.cpp.

Here is the call graph for this function:

operator<<() [67/77]

std::ostream& carl::operator<< ( std::ostream &  os, const UninterpretedFunction &  ufun  )

inline

Prints the given uninterpreted function on the given output stream.

Parameters

os	The output stream to print on.
ufun	The uninterpreted function to print.

Returns

The output stream after printing the given uninterpreted function on it.

Definition at line 91 of file UninterpretedFunction.h.

Here is the call graph for this function:

operator<<() [68/77]

template<typename Number >

std::ostream& carl::operator<<	(	std::ostream &	os,
		const UpperBound< Number > &	lb
	)

Definition at line 111 of file Interval.h.

operator<<() [69/77]

std::ostream & carl::operator<<	(	std::ostream &	os,
		const UTerm &	ut
	)

Prints the given uninterpreted term on the given output stream.

Parameters

os	The output stream to print on.
ut	The uninterpreted term to print.

Returns

The output stream after printing the given uninterpreted term on it.

Definition at line 65 of file UTerm.cpp.

Here is the call graph for this function:

operator<<() [70/77]

template<typename Poly >

std::ostream& carl::operator<<	(	std::ostream &	os,
		const VariableAssignment< Poly > &	va
	)

Definition at line 60 of file VariableAssignment.h.

Here is the call graph for this function:

operator<<() [71/77]

template<typename Poly >

std::ostream& carl::operator<<	(	std::ostream &	os,
		const VariableComparison< Poly > &	vc
	)

Definition at line 205 of file VariableComparison.h.

Here is the call graph for this function:

operator<<() [72/77]

std::ostream& carl::operator<< ( std::ostream &  os, const VariableType &  t  )

inline

Streaming operator for VariableType.

Parameters

os	Output Stream.
t	VariableType.

Returns

os.

Definition at line 43 of file Variable.h.

Here is the call graph for this function:

operator<<() [73/77]

std::ostream& carl::operator<< ( std::ostream &  os, Definiteness  d  )

inline

Definition at line 29 of file Definiteness.h.

operator<<() [74/77]

std::ostream& carl::operator<< ( std::ostream &  os, FormulaType  t  )

inline

Definition at line 87 of file FormulaContent.h.

Here is the call graph for this function:

operator<<() [75/77]

std::ostream& carl::operator<< ( std::ostream &  os, UVariable  uvar  )

inline

Prints the given uninterpreted variable on the given output stream.

Parameters

os	The output stream to print on.
uvar	The uninterpreted variable to print.

Returns

The output stream after printing the given uninterpreted variable on it.

Definition at line 74 of file UVariable.h.

Here is the call graph for this function:

operator<<() [76/77]

std::ostream& carl::operator<< ( std::ostream &  os, Variable  rhs  )

inline

Streaming operator for Variable.

Parameters

os	Output stream.
rhs	Variable.

Returns

os

Definition at line 213 of file Variable.h.

Here is the call graph for this function:

operator<<() [77/77]

template<class E , bool FI>

std::ostream& carl::operator<<	(	std::ostream &	out,
		const CompactTree< E, FI > &	tree
	)

Definition at line 206 of file CompactTree.h.

operator<=() [1/41]

template<typename P >

bool carl::operator<=	(	const BasicConstraint< P > &	lhs,
		const BasicConstraint< P > &	rhs
	)

Definition at line 123 of file BasicConstraint.h.

operator<=() [2/41]

template<typename C , typename O , typename P >

bool carl::operator<= ( const C &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first argument is less or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs <= rhs

Definition at line 347 of file MultivariatePolynomial_operators.h.

operator<=() [3/41]

template<typename Coeff >

bool carl::operator<= ( const Coeff &  lhs, const Term< Coeff > &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 478 of file Term.h.

operator<=() [4/41]

bool carl::operator<= ( const Condition &  lhs, const Condition &  rhs  )

inline

Check whether the bits of one condition are always set if the corresponding bit of another condition is set.

Essentially checks for an implication.

Parameters

lhs	The first condition.
rhs	The second condition.

Returns

true, if all bits of lhs are set if the corresponding bit of rhs are set; false, otherwise.

Definition at line 45 of file Condition.h.

operator<=() [5/41]

template<typename P >

bool carl::operator<=	(	const Constraint< P > &	lhs,
		const Constraint< P > &	rhs
	)

Definition at line 303 of file Constraint.h.

operator<=() [6/41]

template<typename P >

bool carl::operator<= ( const FactorizedPolynomial< P > &  _lhs, const FactorizedPolynomial< P > &  _rhs  )

inline

Checks if the first arguments is less or equal than the second.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs <= _rhs

Definition at line 869 of file FactorizedPolynomial.h.

operator<=() [7/41]

template<typename P >

bool carl::operator<= ( const FactorizedPolynomial< P > &  _lhs, const typename FactorizedPolynomial< P >::CoeffType &  _rhs  )

inline

Checks if the first arguments is less or equal than the second.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs <= _rhs

Definition at line 875 of file FactorizedPolynomial.h.

operator<=() [8/41]

template<typename Number >

bool carl::operator<= ( const Interval< Number > &  lhs, const Interval< Number > &  rhs  )

inline

Operator for the comparison of two intervals.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

True if the righthand side has maximal one intersection with the lefthand side at the upper bound of lhs.

Definition at line 209 of file operators.h.

Here is the call graph for this function:

operator<=() [9/41]

template<typename Number >

bool carl::operator<= ( const Interval< Number > &  lhs, const Number &  rhs  )

inline

Definition at line 223 of file operators.h.

Here is the call graph for this function:

operator<=() [10/41]

template<typename Number >

bool carl::operator<= ( const LowerBound< Number > &  lhs, const LowerBound< Number > &  rhs  )

inline

Definition at line 28 of file operators.h.

operator<=() [11/41]

template<typename Number >

bool carl::operator<= ( const LowerBound< Number > &  lhs, const UpperBound< Number > &  rhs  )

inline

Definition at line 43 of file operators.h.

operator<=() [12/41]

bool carl::operator<= ( const Monomial::Arg &  lhs, const Monomial::Arg &  rhs  )

inline

Compares two arguments where one is a Monomial and the other is either a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 561 of file Monomial.h.

operator<=() [13/41]

template<typename C , typename O , typename P >

bool carl::operator<= ( const Monomial::Arg &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first argument is less or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs <= rhs

Definition at line 339 of file MultivariatePolynomial_operators.h.

operator<=() [14/41]

template<typename Coeff >

bool carl::operator<= ( const Monomial::Arg &  lhs, const Term< Coeff > &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 470 of file Term.h.

operator<=() [15/41]

bool carl::operator<= ( const Monomial::Arg &  lhs, Variable  rhs  )

inline

Compares two arguments where one is a Monomial and the other is either a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 565 of file Monomial.h.

operator<=() [16/41]

template<typename C , typename O , typename P >

bool carl::operator<= ( const MultivariatePolynomial< C, O, P > &  lhs, const C &  rhs  )

inline

Checks if the first argument is less or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs <= rhs

Definition at line 331 of file MultivariatePolynomial_operators.h.

operator<=() [17/41]

template<typename C , typename O , typename P >

bool carl::operator<= ( const MultivariatePolynomial< C, O, P > &  lhs, const Monomial::Arg &  rhs  )

inline

Checks if the first argument is less or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs <= rhs

Definition at line 323 of file MultivariatePolynomial_operators.h.

operator<=() [18/41]

template<typename C , typename O , typename P >

bool carl::operator<= ( const MultivariatePolynomial< C, O, P > &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first argument is less or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs <= rhs

Definition at line 315 of file MultivariatePolynomial_operators.h.

operator<=() [19/41]

template<typename C , typename O , typename P >

bool carl::operator<= ( const MultivariatePolynomial< C, O, P > &  lhs, const Term< C > &  rhs  )

inline

Checks if the first argument is less or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs <= rhs

Definition at line 319 of file MultivariatePolynomial_operators.h.

operator<=() [20/41]

template<typename C , typename O , typename P >

bool carl::operator<= ( const MultivariatePolynomial< C, O, P > &  lhs, const UnivariatePolynomial< C > &  rhs  )

inline

Checks if the first argument is less or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs <= rhs

Definition at line 356 of file MultivariatePolynomial_operators.h.

operator<=() [21/41]

template<typename C , typename O , typename P >

bool carl::operator<= ( const MultivariatePolynomial< C, O, P > &  lhs, const UnivariatePolynomial< MultivariatePolynomial< C >> &  rhs  )

inline

Checks if the first argument is less or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs <= rhs

Definition at line 364 of file MultivariatePolynomial_operators.h.

operator<=() [22/41]

template<typename C , typename O , typename P >

bool carl::operator<= ( const MultivariatePolynomial< C, O, P > &  lhs, Variable  rhs  )

inline

Checks if the first argument is less or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs <= rhs

Definition at line 327 of file MultivariatePolynomial_operators.h.

operator<=() [23/41]

template<typename N >

bool carl::operator<=	(	const N &	lhs,
		const ThomEncoding< N > &	rhs
	)

Definition at line 588 of file ThomEncoding.h.

operator<=() [24/41]

template<typename Number >

bool carl::operator<= ( const Number &  lhs, const Interval< Number > &  rhs  )

inline

Definition at line 228 of file operators.h.

Here is the call graph for this function:

operator<=() [25/41]

template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>

bool carl::operator<=	(	const Number &	lhs,
		const RAN &	rhs
	)

Definition at line 59 of file Operations.h.

operator<=() [26/41]

template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>

bool carl::operator<=	(	const RAN &	lhs,
		const Number &	rhs
	)

Definition at line 34 of file Operations.h.

Here is the call graph for this function:

operator<=() [27/41]

template<typename RAN , EnableIf< is_ran_type< RAN >> = dummy>

bool carl::operator<=	(	const RAN &	lhs,
		const RAN &	rhs
	)

Definition at line 84 of file Operations.h.

Here is the call graph for this function:

operator<=() [28/41]

template<typename C , typename O , typename P >

bool carl::operator<= ( const Term< C > &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first argument is less or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs <= rhs

Definition at line 335 of file MultivariatePolynomial_operators.h.

operator<=() [29/41]

template<typename Coeff >

bool carl::operator<= ( const Term< Coeff > &  lhs, const Coeff &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 466 of file Term.h.

operator<=() [30/41]

template<typename Coeff >

bool carl::operator<= ( const Term< Coeff > &  lhs, const Monomial::Arg &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 458 of file Term.h.

operator<=() [31/41]

template<typename Coeff >

bool carl::operator<= ( const Term< Coeff > &  lhs, const Term< Coeff > &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 454 of file Term.h.

operator<=() [32/41]

template<typename Coeff >

bool carl::operator<= ( const Term< Coeff > &  lhs, Variable  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 462 of file Term.h.

operator<=() [33/41]

template<typename N >

bool carl::operator<=	(	const ThomEncoding< N > &	lhs,
		const N &	rhs
	)

Definition at line 575 of file ThomEncoding.h.

operator<=() [34/41]

template<typename N >

bool carl::operator<=	(	const ThomEncoding< N > &	lhs,
		const ThomEncoding< N > &	rhs
	)

Definition at line 561 of file ThomEncoding.h.

operator<=() [35/41]

template<typename P >

bool carl::operator<= ( const typename FactorizedPolynomial< P >::CoeffType &  _lhs, const FactorizedPolynomial< P > &  _rhs  )

inline

Checks if the first arguments is less or equal than the second.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs <= _rhs

Definition at line 881 of file FactorizedPolynomial.h.

operator<=() [36/41]

template<typename C , typename O , typename P >

bool carl::operator<= ( const UnivariatePolynomial< C > &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first argument is less or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs <= rhs

Definition at line 352 of file MultivariatePolynomial_operators.h.

operator<=() [37/41]

template<typename C , typename O , typename P >

bool carl::operator<= ( const UnivariatePolynomial< MultivariatePolynomial< C >> &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first argument is less or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs <= rhs

Definition at line 360 of file MultivariatePolynomial_operators.h.

operator<=() [38/41]

template<typename Number >

bool carl::operator<= ( const UpperBound< Number > &  lhs, const UpperBound< Number > &  rhs  )

inline

Definition at line 66 of file operators.h.

operator<=() [39/41]

bool carl::operator<= ( Variable  lhs, const Monomial::Arg &  rhs  )

inline

Compares two arguments where one is a Monomial and the other is either a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 569 of file Monomial.h.

operator<=() [40/41]

template<typename C , typename O , typename P >

bool carl::operator<= ( Variable  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first argument is less or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs <= rhs

Definition at line 343 of file MultivariatePolynomial_operators.h.

operator<=() [41/41]

template<typename Coeff >

bool carl::operator<= ( Variable  lhs, const Term< Coeff > &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 474 of file Term.h.

operator==() [1/71]

template<typename P >

bool carl::operator==	(	const BasicConstraint< P > &	lhs,
		const BasicConstraint< P > &	rhs
	)

Definition at line 107 of file BasicConstraint.h.

Here is the call graph for this function:

operator==() [2/71]

bool carl::operator==	(	const BitVector &	lhs,
		const BitVector &	rhs
	)

Definition at line 37 of file BitVector.cpp.

operator==() [3/71]

bool carl::operator==	(	const BitVector::forward_iterator &	fi1,
		const BitVector::forward_iterator &	fi2
	)

Definition at line 42 of file BitVector.cpp.

operator==() [4/71]

bool carl::operator==	(	const BVConstraint &	lhs,
		const BVConstraint &	rhs
	)

Definition at line 19 of file BVConstraint.cpp.

Here is the call graph for this function:

operator==() [5/71]

bool carl::operator==	(	const BVTerm &	lhs,
		const BVTerm &	rhs
	)

Definition at line 130 of file BVTerm.cpp.

operator==() [6/71]

bool carl::operator== ( const BVTermContent &  lhs, const BVTermContent &  rhs  )

inline

Definition at line 209 of file BVTermContent.h.

Here is the call graph for this function:

operator==() [7/71]

bool carl::operator== ( const BVValue &  lhs, const BVValue &  rhs  )

inline

Definition at line 147 of file BVValue.h.

Here is the call graph for this function:

operator==() [8/71]

bool carl::operator== ( const BVVariable &  lhs, const BVVariable &  rhs  )

inline

Definition at line 70 of file BVVariable.h.

Here is the call graph for this function:

operator==() [9/71]

bool carl::operator== ( const BVVariable &  lhs, const Variable &  rhs  )

inline

Definition at line 73 of file BVVariable.h.

Here is the call graph for this function:

operator==() [10/71]

template<typename C , typename O , typename P >

bool carl::operator== ( const C &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the two arguments are equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs == rhs

Definition at line 79 of file MultivariatePolynomial_operators.h.

operator==() [11/71]

bool carl::operator== ( const carlVariables &  lhs, const carlVariables &  rhs  )

inline

Definition at line 208 of file Variables.h.

operator==() [12/71]

template<typename Coeff >

bool carl::operator== ( const Coeff &  lhs, const Term< Coeff > &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 405 of file Term.h.

operator==() [13/71]

template<typename P >

bool carl::operator==	(	const Constraint< P > &	lhs,
		const Constraint< P > &	rhs
	)

Definition at line 288 of file Constraint.h.

operator==() [14/71]

template<typename Coeff , typename Ordering , typename Policies >

bool carl::operator==	(	const ContextPolynomial< Coeff, Ordering, Policies > &	lhs,
		const ContextPolynomial< Coeff, Ordering, Policies > &	rhs
	)

Definition at line 145 of file ContextPolynomial.h.

Here is the call graph for this function:

operator==() [15/71]

template<typename P >

bool carl::operator==	(	const FactorizedPolynomial< P > &	_lhs,
		const FactorizedPolynomial< P > &	_rhs
	)

Checks if the two arguments are equal.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs == _rhs

operator==() [16/71]

template<typename P >

bool carl::operator==	(	const FactorizedPolynomial< P > &	_lhs,
		const typename FactorizedPolynomial< P >::CoeffType &	_rhs
	)

Checks if the two arguments are equal.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs == _rhs

operator==() [17/71]

template<>

bool carl::operator== ( const Interval< double > &  lhs, const Interval< double > &  rhs  )

inline

Definition at line 94 of file operators.h.

Here is the call graph for this function:

operator==() [18/71]

template<typename Number >

bool carl::operator== ( const Interval< Number > &  lhs, const Interval< Number > &  rhs  )

inline

Operator for the comparison of two intervals.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

True if both intervals are equal.

Definition at line 88 of file operators.h.

Here is the call graph for this function:

operator==() [19/71]

template<typename Number >

bool carl::operator== ( const Interval< Number > &  lhs, const Number &  rhs  )

inline

Definition at line 104 of file operators.h.

Here is the call graph for this function:

operator==() [20/71]

template<typename Rational , typename Poly >

bool carl::operator==	(	const ModelValue< Rational, Poly > &	lhs,
		const ModelValue< Rational, Poly > &	rhs
	)

Check if two Assignments are equal.

Two Assignments are considered equal, if both are either bool or not bool and their value is the same.

If both Assignments are not bools, the check may return false although they represent the same value. If both are numbers in different representations, this comparison is only done as a "best effort".

Parameters

lhs	First Assignment.
rhs	Second Assignment.

Returns

lhs == rhs.

Definition at line 295 of file ModelValue.h.

operator==() [21/71]

bool carl::operator== ( const ModelVariable &  lhs, const ModelVariable &  rhs  )

inline

Return true if lhs is equal to rhs.

Definition at line 105 of file ModelVariable.h.

operator==() [22/71]

bool carl::operator== ( const Monomial &  lhs, const Monomial &  rhs  )

inline

Compares two arguments where one is a Monomial and the other is either a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 489 of file Monomial.h.

Here is the call graph for this function:

operator==() [23/71]

bool carl::operator== ( const Monomial::Arg &  lhs, const Monomial::Arg &  rhs  )

inline

Compares two arguments where one is a Monomial and the other is either a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 503 of file Monomial.h.

operator==() [24/71]

template<typename C , typename O , typename P >

bool carl::operator== ( const Monomial::Arg &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the two arguments are equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs == rhs

Definition at line 71 of file MultivariatePolynomial_operators.h.

operator==() [25/71]

template<typename Coeff >

bool carl::operator== ( const Monomial::Arg &  lhs, const Term< Coeff > &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 397 of file Term.h.

operator==() [26/71]

bool carl::operator== ( const Monomial::Arg &  lhs, Variable  rhs  )

inline

Compares two arguments where one is a Monomial and the other is either a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 512 of file Monomial.h.

operator==() [27/71]

template<typename C , typename O , typename P >

bool carl::operator== ( const MultivariatePolynomial< C, O, P > &  lhs, const C &  rhs  )

inline

Checks if the two arguments are equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs == rhs

Definition at line 59 of file MultivariatePolynomial_operators.h.

Here is the call graph for this function:

operator==() [28/71]

template<typename C , typename O , typename P >

bool carl::operator== ( const MultivariatePolynomial< C, O, P > &  lhs, const Monomial::Arg &  rhs  )

inline

Checks if the two arguments are equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs == rhs

Definition at line 47 of file MultivariatePolynomial_operators.h.

Here is the call graph for this function:

operator==() [29/71]

template<typename C , typename O , typename P >

bool carl::operator== ( const MultivariatePolynomial< C, O, P > &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the two arguments are equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs == rhs

Definition at line 16 of file MultivariatePolynomial_operators.h.

Here is the call graph for this function:

operator==() [30/71]

template<typename C , typename O , typename P >

bool carl::operator== ( const MultivariatePolynomial< C, O, P > &  lhs, const Term< C > &  rhs  )

inline

Checks if the two arguments are equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs == rhs

Definition at line 41 of file MultivariatePolynomial_operators.h.

Here is the call graph for this function:

operator==() [31/71]

template<typename C , typename O , typename P >

bool carl::operator== ( const MultivariatePolynomial< C, O, P > &  lhs, const UnivariatePolynomial< C > &  rhs  )

inline

Checks if the two arguments are equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs == rhs

Definition at line 89 of file MultivariatePolynomial_operators.h.

operator==() [32/71]

template<typename C , typename O , typename P >

bool carl::operator== ( const MultivariatePolynomial< C, O, P > &  lhs, const UnivariatePolynomial< MultivariatePolynomial< C >> &  rhs  )

inline

Checks if the two arguments are equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs == rhs

Definition at line 98 of file MultivariatePolynomial_operators.h.

operator==() [33/71]

template<typename C , typename O , typename P , DisableIf< std::is_integral< C >> = dummy>

bool carl::operator== ( const MultivariatePolynomial< C, O, P > &  lhs, int  rhs  )

inline

Checks if the two arguments are equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs == rhs

Definition at line 63 of file MultivariatePolynomial_operators.h.

Here is the call graph for this function:

operator==() [34/71]

template<typename C , typename O , typename P >

bool carl::operator== ( const MultivariatePolynomial< C, O, P > &  lhs, Variable  rhs  )

inline

Checks if the two arguments are equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs == rhs

Definition at line 53 of file MultivariatePolynomial_operators.h.

Here is the call graph for this function:

operator==() [35/71]

template<typename Poly >

bool carl::operator== ( const MultivariateRoot< Poly > &  lhs, const MultivariateRoot< Poly > &  rhs  )

inline

Definition at line 95 of file MultivariateRoot.h.

Here is the call graph for this function:

operator==() [36/71]

template<typename N >

bool carl::operator==	(	const N &	lhs,
		const ThomEncoding< N > &	rhs
	)

Definition at line 594 of file ThomEncoding.h.

operator==() [37/71]

template<typename Number >

bool carl::operator== ( const Number &  lhs, const Interval< Number > &  rhs  )

inline

Definition at line 108 of file operators.h.

operator==() [38/71]

template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>

bool carl::operator==	(	const Number &	lhs,
		const RAN &	rhs
	)

Definition at line 51 of file Operations.h.

operator==() [39/71]

template<typename Number >

bool carl::operator==	(	const Number &	lhs,
		const RealAlgebraicNumberThom< Number > &	rhs
	)

Definition at line 190 of file ran_thom.h.

operator==() [40/71]

template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>

bool carl::operator==	(	const RAN &	lhs,
		const Number &	rhs
	)

Definition at line 26 of file Operations.h.

Here is the call graph for this function:

operator==() [41/71]

template<typename RAN , EnableIf< is_ran_type< RAN >> = dummy>

bool carl::operator==	(	const RAN &	lhs,
		const RAN &	rhs
	)

Definition at line 76 of file Operations.h.

Here is the call graph for this function:

operator==() [42/71]

template<typename Number >

bool carl::operator==	(	const RealAlgebraicNumberThom< Number > &	lhs,
		const Number &	rhs
	)

Definition at line 185 of file ran_thom.h.

operator==() [43/71]

template<typename Number >

bool carl::operator==	(	const RealAlgebraicNumberThom< Number > &	lhs,
		const RealAlgebraicNumberThom< Number > &	rhs
	)

Definition at line 179 of file ran_thom.h.

operator==() [44/71]

bool carl::operator== ( const SortValue &  lhs, const SortValue &  rhs  )

inline

Compares two sort values for equality.

Definition at line 74 of file SortValue.h.

Here is the call graph for this function:

operator==() [45/71]

bool carl::operator== ( const std::pair< Variable, std::size_t > &  p, Variable  v  )

inline

Compare a pair of variable and exponent with a variable.

Returns true, if both variables are the same.

Parameters

p	Pair of variable and exponent.
v	Variable.

Returns

p.first == v

Definition at line 38 of file Monomial.h.

operator==() [46/71]

template<typename C , typename O , typename P >

bool carl::operator== ( const Term< C > &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the two arguments are equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs == rhs

Definition at line 67 of file MultivariatePolynomial_operators.h.

operator==() [47/71]

template<typename Coeff >

bool carl::operator== ( const Term< Coeff > &  lhs, const Coeff &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

operator==() [48/71]

template<typename Coeff >

bool carl::operator== ( const Term< Coeff > &  lhs, const Monomial &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

operator==() [49/71]

template<typename Coeff >

bool carl::operator== ( const Term< Coeff > &  lhs, const Term< Coeff > &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

operator==() [50/71]

template<typename Coeff >

bool carl::operator== ( const Term< Coeff > &  lhs, Variable  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

operator==() [51/71]

template<typename N >

bool carl::operator==	(	const ThomEncoding< N > &	lhs,
		const N &	rhs
	)

Definition at line 581 of file ThomEncoding.h.

operator==() [52/71]

template<typename N >

bool carl::operator==	(	const ThomEncoding< N > &	lhs,
		const ThomEncoding< N > &	rhs
	)

Definition at line 567 of file ThomEncoding.h.

operator==() [53/71]

template<typename T , class I >

bool carl::operator==	(	const TypeInfoPair< T, I > &	_tipA,
		const TypeInfoPair< T, I > &	_tipB
	)

Definition at line 24 of file Cache.h.

operator==() [54/71]

template<typename P >

bool carl::operator== ( const typename FactorizedPolynomial< P >::CoeffType &  _lhs, const FactorizedPolynomial< P > &  _rhs  )

inline

Checks if the two arguments are equal.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs == _rhs

Definition at line 809 of file FactorizedPolynomial.h.

operator==() [55/71]

bool carl::operator== ( const UEquality &  lhs, const UEquality &  rhs  )

inline

Parameters

lhs	The left hand side.
rhs	The right hand side.

Returns

true, if lhs and rhs are equal.

Definition at line 114 of file UEquality.h.

Here is the call graph for this function:

operator==() [56/71]

bool carl::operator== ( const UFContent &  lhs, const UFContent &  rhs  )

inline

Parameters

lhs	Left UFContent.
rhs	Right UFContent.

Returns

true, if lhs and rhs are the same.

Definition at line 82 of file UFManager.h.

Here is the call graph for this function:

operator==() [57/71]

bool carl::operator== ( const UFInstance &  lhs, const UFInstance &  rhs  )

inline

Parameters

lhs	The left function instance.
rhs	The right function instance.

Returns

true, if lhs == rhs.

Definition at line 72 of file UFInstance.h.

Here is the call graph for this function:

operator==() [58/71]

bool carl::operator== ( const UFModel &  lhs, const UFModel &  rhs  )

inline

Compares two UFModel objects for equality.

Returns

true, if the two uninterpreted function models are equal.

Definition at line 50 of file UFModel.h.

Here is the call graph for this function:

operator==() [59/71]

bool carl::operator== ( const UninterpretedFunction &  lhs, const UninterpretedFunction &  rhs  )

inline

Check whether two uninterpreted functions are equal.

Returns

true, if the two given uninterpreted functions are equal.

Definition at line 73 of file UninterpretedFunction.h.

Here is the call graph for this function:

operator==() [60/71]

template<typename C , typename O , typename P >

bool carl::operator== ( const UnivariatePolynomial< C > &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the two arguments are equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs == rhs

Definition at line 84 of file MultivariatePolynomial_operators.h.

operator==() [61/71]

template<typename C , typename O , typename P >

bool carl::operator== ( const UnivariatePolynomial< MultivariatePolynomial< C >> &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the two arguments are equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs == rhs

Definition at line 93 of file MultivariatePolynomial_operators.h.

operator==() [62/71]

bool carl::operator==	(	const UTerm &	lhs,
		const UTerm &	rhs
	)

Parameters

lhs	The uninterpreted term to the left.
rhs	The uninterpreted term to the right.

Returns

true, if the given uninterpreted terms are equal.

Definition at line 44 of file UTerm.cpp.

Here is the call graph for this function:

operator==() [63/71]

bool carl::operator== ( const Variable &  lhs, const BVVariable &  rhs  )

inline

Definition at line 76 of file BVVariable.h.

Here is the call graph for this function:

operator==() [64/71]

template<typename Poly >

bool carl::operator==	(	const VariableAssignment< Poly > &	lhs,
		const VariableAssignment< Poly > &	rhs
	)

Definition at line 52 of file VariableAssignment.h.

operator==() [65/71]

template<typename Poly >

bool carl::operator==	(	const VariableComparison< Poly > &	lhs,
		const VariableComparison< Poly > &	rhs
	)

Definition at line 194 of file VariableComparison.h.

Here is the call graph for this function:

operator==() [66/71]

bool carl::operator== ( InfinityValue  lhs, InfinityValue  rhs  )

inline

Definition at line 40 of file ModelValue.h.

operator==() [67/71]

bool carl::operator== ( Sort  lhs, Sort  rhs  )

inline

Parameters

lhs	The left sort.
rhs	The right sort.

Returns

true, if the sorts are the same.

Definition at line 70 of file Sort.h.

Here is the call graph for this function:

operator==() [68/71]

bool carl::operator== ( UVariable  lhs, UVariable  rhs  )

inline

Parameters

lhs	The left variable.
rhs	The right variable.

Returns

true, if the variable are equal.

Definition at line 83 of file UVariable.h.

Here is the call graph for this function:

operator==() [69/71]

bool carl::operator== ( Variable  lhs, const Monomial::Arg &  rhs  )

inline

Compares two arguments where one is a Monomial and the other is either a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 518 of file Monomial.h.

operator==() [70/71]

template<typename C , typename O , typename P >

bool carl::operator== ( Variable  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the two arguments are equal.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs == rhs

Definition at line 75 of file MultivariatePolynomial_operators.h.

operator==() [71/71]

template<typename Coeff >

bool carl::operator== ( Variable  lhs, const Term< Coeff > &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 401 of file Term.h.

operator>() [1/37]

template<typename P >

bool carl::operator>	(	const BasicConstraint< P > &	lhs,
		const BasicConstraint< P > &	rhs
	)

Definition at line 128 of file BasicConstraint.h.

operator>() [2/37]

template<typename C , typename O , typename P >

bool carl::operator> ( const C &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first argument is greater than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs > rhs

Definition at line 284 of file MultivariatePolynomial_operators.h.

operator>() [3/37]

template<typename Coeff >

bool carl::operator> ( const Coeff &  lhs, const Term< Coeff > &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 507 of file Term.h.

operator>() [4/37]

template<typename P >

bool carl::operator>	(	const Constraint< P > &	lhs,
		const Constraint< P > &	rhs
	)

Definition at line 308 of file Constraint.h.

operator>() [5/37]

template<typename P >

bool carl::operator> ( const FactorizedPolynomial< P > &  _lhs, const FactorizedPolynomial< P > &  _rhs  )

inline

Checks if the first arguments is greater than the second.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs > _rhs

Definition at line 896 of file FactorizedPolynomial.h.

operator>() [6/37]

template<typename P >

bool carl::operator> ( const FactorizedPolynomial< P > &  _lhs, const typename FactorizedPolynomial< P >::CoeffType &  _rhs  )

inline

Checks if the first arguments is greater than the second.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs > _rhs

Definition at line 902 of file FactorizedPolynomial.h.

operator>() [7/37]

template<typename Number >

bool carl::operator> ( const Interval< Number > &  lhs, const Interval< Number > &  rhs  )

inline

Operator for the comparison of two intervals.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

True if the lefthand side is larger than the righthand side.

Definition at line 188 of file operators.h.

operator>() [8/37]

template<typename Number >

bool carl::operator> ( const Interval< Number > &  lhs, const Number &  rhs  )

inline

Definition at line 192 of file operators.h.

operator>() [9/37]

bool carl::operator> ( const Monomial::Arg &  lhs, const Monomial::Arg &  rhs  )

inline

Compares two arguments where one is a Monomial and the other is either a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 573 of file Monomial.h.

operator>() [10/37]

template<typename C , typename O , typename P >

bool carl::operator> ( const Monomial::Arg &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first argument is greater than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs > rhs

Definition at line 276 of file MultivariatePolynomial_operators.h.

operator>() [11/37]

template<typename Coeff >

bool carl::operator> ( const Monomial::Arg &  lhs, const Term< Coeff > &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 499 of file Term.h.

operator>() [12/37]

bool carl::operator> ( const Monomial::Arg &  lhs, Variable  rhs  )

inline

Compares two arguments where one is a Monomial and the other is either a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 577 of file Monomial.h.

operator>() [13/37]

template<typename C , typename O , typename P >

bool carl::operator> ( const MultivariatePolynomial< C, O, P > &  lhs, const C &  rhs  )

inline

Checks if the first argument is greater than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs > rhs

Definition at line 268 of file MultivariatePolynomial_operators.h.

operator>() [14/37]

template<typename C , typename O , typename P >

bool carl::operator> ( const MultivariatePolynomial< C, O, P > &  lhs, const Monomial::Arg &  rhs  )

inline

Checks if the first argument is greater than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs > rhs

Definition at line 260 of file MultivariatePolynomial_operators.h.

operator>() [15/37]

template<typename C , typename O , typename P >

bool carl::operator> ( const MultivariatePolynomial< C, O, P > &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first argument is greater than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs > rhs

Definition at line 252 of file MultivariatePolynomial_operators.h.

operator>() [16/37]

template<typename C , typename O , typename P >

bool carl::operator> ( const MultivariatePolynomial< C, O, P > &  lhs, const Term< C > &  rhs  )

inline

Checks if the first argument is greater than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs > rhs

Definition at line 256 of file MultivariatePolynomial_operators.h.

operator>() [17/37]

template<typename C , typename O , typename P >

bool carl::operator> ( const MultivariatePolynomial< C, O, P > &  lhs, const UnivariatePolynomial< C > &  rhs  )

inline

Checks if the first argument is greater than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs > rhs

Definition at line 293 of file MultivariatePolynomial_operators.h.

operator>() [18/37]

template<typename C , typename O , typename P >

bool carl::operator> ( const MultivariatePolynomial< C, O, P > &  lhs, const UnivariatePolynomial< MultivariatePolynomial< C >> &  rhs  )

inline

Checks if the first argument is greater than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs > rhs

Definition at line 301 of file MultivariatePolynomial_operators.h.

operator>() [19/37]

template<typename C , typename O , typename P >

bool carl::operator> ( const MultivariatePolynomial< C, O, P > &  lhs, Variable  rhs  )

inline

Checks if the first argument is greater than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs > rhs

Definition at line 264 of file MultivariatePolynomial_operators.h.

operator>() [20/37]

template<typename N >

bool carl::operator>	(	const N &	lhs,
		const ThomEncoding< N > &	rhs
	)

Definition at line 590 of file ThomEncoding.h.

operator>() [21/37]

template<typename Number >

bool carl::operator> ( const Number &  lhs, const Interval< Number > &  rhs  )

inline

Definition at line 196 of file operators.h.

operator>() [22/37]

template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>

bool carl::operator>	(	const Number &	lhs,
		const RAN &	rhs
	)

Definition at line 71 of file Operations.h.

operator>() [23/37]

template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>

bool carl::operator>	(	const RAN &	lhs,
		const Number &	rhs
	)

Definition at line 46 of file Operations.h.

Here is the call graph for this function:

operator>() [24/37]

template<typename RAN , EnableIf< is_ran_type< RAN >> = dummy>

bool carl::operator>	(	const RAN &	lhs,
		const RAN &	rhs
	)

Definition at line 96 of file Operations.h.

Here is the call graph for this function:

operator>() [25/37]

template<typename C , typename O , typename P >

bool carl::operator> ( const Term< C > &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first argument is greater than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs > rhs

Definition at line 272 of file MultivariatePolynomial_operators.h.

operator>() [26/37]

template<typename Coeff >

bool carl::operator> ( const Term< Coeff > &  lhs, const Coeff &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 495 of file Term.h.

operator>() [27/37]

template<typename Coeff >

bool carl::operator> ( const Term< Coeff > &  lhs, const Monomial::Arg &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 487 of file Term.h.

operator>() [28/37]

template<typename Coeff >

bool carl::operator> ( const Term< Coeff > &  lhs, const Term< Coeff > &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 483 of file Term.h.

operator>() [29/37]

template<typename Coeff >

bool carl::operator> ( const Term< Coeff > &  lhs, Variable  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 491 of file Term.h.

operator>() [30/37]

template<typename N >

bool carl::operator>	(	const ThomEncoding< N > &	lhs,
		const N &	rhs
	)

Definition at line 577 of file ThomEncoding.h.

operator>() [31/37]

template<typename N >

bool carl::operator>	(	const ThomEncoding< N > &	lhs,
		const ThomEncoding< N > &	rhs
	)

Definition at line 563 of file ThomEncoding.h.

operator>() [32/37]

template<typename P >

bool carl::operator> ( const typename FactorizedPolynomial< P >::CoeffType &  _lhs, const FactorizedPolynomial< P > &  _rhs  )

inline

Checks if the first arguments is greater than the second.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs > _rhs

Definition at line 908 of file FactorizedPolynomial.h.

operator>() [33/37]

template<typename C , typename O , typename P >

bool carl::operator> ( const UnivariatePolynomial< C > &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first argument is greater than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs > rhs

Definition at line 289 of file MultivariatePolynomial_operators.h.

operator>() [34/37]

template<typename C , typename O , typename P >

bool carl::operator> ( const UnivariatePolynomial< MultivariatePolynomial< C >> &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first argument is greater than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs > rhs

Definition at line 297 of file MultivariatePolynomial_operators.h.

operator>() [35/37]

bool carl::operator> ( Variable  lhs, const Monomial::Arg &  rhs  )

inline

Compares two arguments where one is a Monomial and the other is either a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 581 of file Monomial.h.

operator>() [36/37]

template<typename C , typename O , typename P >

bool carl::operator> ( Variable  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first argument is greater than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs > rhs

Definition at line 280 of file MultivariatePolynomial_operators.h.

operator>() [37/37]

template<typename Coeff >

bool carl::operator> ( Variable  lhs, const Term< Coeff > &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 503 of file Term.h.

operator>=() [1/37]

template<typename P >

bool carl::operator>=	(	const BasicConstraint< P > &	lhs,
		const BasicConstraint< P > &	rhs
	)

Definition at line 133 of file BasicConstraint.h.

operator>=() [2/37]

template<typename C , typename O , typename P >

bool carl::operator>= ( const C &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first argument is greater or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs >= rhs

Definition at line 410 of file MultivariatePolynomial_operators.h.

operator>=() [3/37]

template<typename Coeff >

bool carl::operator>= ( const Coeff &  lhs, const Term< Coeff > &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 536 of file Term.h.

operator>=() [4/37]

template<typename P >

bool carl::operator>=	(	const Constraint< P > &	lhs,
		const Constraint< P > &	rhs
	)

Definition at line 313 of file Constraint.h.

operator>=() [5/37]

template<typename P >

bool carl::operator>= ( const FactorizedPolynomial< P > &  _lhs, const FactorizedPolynomial< P > &  _rhs  )

inline

Checks if the first arguments is greater or equal than the second.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs >= _rhs

Definition at line 923 of file FactorizedPolynomial.h.

operator>=() [6/37]

template<typename P >

bool carl::operator>= ( const FactorizedPolynomial< P > &  _lhs, const typename FactorizedPolynomial< P >::CoeffType &  _rhs  )

inline

Checks if the first arguments is greater or equal than the second.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs >= _rhs

Definition at line 929 of file FactorizedPolynomial.h.

operator>=() [7/37]

template<typename Number >

bool carl::operator>= ( const Interval< Number > &  lhs, const Interval< Number > &  rhs  )

inline

Operator for the comparison of two intervals.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

True if the lefthand side has maximal one intersection with the righthand side at the lower bound of lhs.

Definition at line 241 of file operators.h.

operator>=() [8/37]

template<typename Number >

bool carl::operator>= ( const Interval< Number > &  lhs, const Number &  rhs  )

inline

Definition at line 245 of file operators.h.

operator>=() [9/37]

bool carl::operator>= ( const Monomial::Arg &  lhs, const Monomial::Arg &  rhs  )

inline

Compares two arguments where one is a Monomial and the other is either a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 585 of file Monomial.h.

operator>=() [10/37]

template<typename C , typename O , typename P >

bool carl::operator>= ( const Monomial::Arg &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first argument is greater or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs >= rhs

Definition at line 402 of file MultivariatePolynomial_operators.h.

operator>=() [11/37]

template<typename Coeff >

bool carl::operator>= ( const Monomial::Arg &  lhs, const Term< Coeff > &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 528 of file Term.h.

operator>=() [12/37]

bool carl::operator>= ( const Monomial::Arg &  lhs, Variable  rhs  )

inline

Compares two arguments where one is a Monomial and the other is either a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 589 of file Monomial.h.

operator>=() [13/37]

template<typename C , typename O , typename P >

bool carl::operator>= ( const MultivariatePolynomial< C, O, P > &  lhs, const C &  rhs  )

inline

Checks if the first argument is greater or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs >= rhs

Definition at line 394 of file MultivariatePolynomial_operators.h.

operator>=() [14/37]

template<typename C , typename O , typename P >

bool carl::operator>= ( const MultivariatePolynomial< C, O, P > &  lhs, const Monomial::Arg &  rhs  )

inline

Checks if the first argument is greater or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs >= rhs

Definition at line 386 of file MultivariatePolynomial_operators.h.

operator>=() [15/37]

template<typename C , typename O , typename P >

bool carl::operator>= ( const MultivariatePolynomial< C, O, P > &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first argument is greater or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs >= rhs

Definition at line 378 of file MultivariatePolynomial_operators.h.

operator>=() [16/37]

template<typename C , typename O , typename P >

bool carl::operator>= ( const MultivariatePolynomial< C, O, P > &  lhs, const Term< C > &  rhs  )

inline

Checks if the first argument is greater or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs >= rhs

Definition at line 382 of file MultivariatePolynomial_operators.h.

operator>=() [17/37]

template<typename C , typename O , typename P >

bool carl::operator>= ( const MultivariatePolynomial< C, O, P > &  lhs, const UnivariatePolynomial< C > &  rhs  )

inline

Checks if the first argument is greater or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs >= rhs

Definition at line 419 of file MultivariatePolynomial_operators.h.

operator>=() [18/37]

template<typename C , typename O , typename P >

bool carl::operator>= ( const MultivariatePolynomial< C, O, P > &  lhs, const UnivariatePolynomial< MultivariatePolynomial< C >> &  rhs  )

inline

Checks if the first argument is greater or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs >= rhs

Definition at line 427 of file MultivariatePolynomial_operators.h.

operator>=() [19/37]

template<typename C , typename O , typename P >

bool carl::operator>= ( const MultivariatePolynomial< C, O, P > &  lhs, Variable  rhs  )

inline

Checks if the first argument is greater or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs >= rhs

Definition at line 390 of file MultivariatePolynomial_operators.h.

operator>=() [20/37]

template<typename N >

bool carl::operator>=	(	const N &	lhs,
		const ThomEncoding< N > &	rhs
	)

Definition at line 592 of file ThomEncoding.h.

operator>=() [21/37]

template<typename Number >

bool carl::operator>= ( const Number &  lhs, const Interval< Number > &  rhs  )

inline

Definition at line 249 of file operators.h.

operator>=() [22/37]

template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>

bool carl::operator>=	(	const Number &	lhs,
		const RAN &	rhs
	)

Definition at line 63 of file Operations.h.

operator>=() [23/37]

template<typename Number , typename RAN , typename = std::enable_if_t<is_ran_type<RAN>::value>>

bool carl::operator>=	(	const RAN &	lhs,
		const Number &	rhs
	)

Definition at line 38 of file Operations.h.

Here is the call graph for this function:

operator>=() [24/37]

template<typename RAN , EnableIf< is_ran_type< RAN >> = dummy>

bool carl::operator>=	(	const RAN &	lhs,
		const RAN &	rhs
	)

Definition at line 88 of file Operations.h.

Here is the call graph for this function:

operator>=() [25/37]

template<typename C , typename O , typename P >

bool carl::operator>= ( const Term< C > &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first argument is greater or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs >= rhs

Definition at line 398 of file MultivariatePolynomial_operators.h.

operator>=() [26/37]

template<typename Coeff >

bool carl::operator>= ( const Term< Coeff > &  lhs, const Coeff &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 524 of file Term.h.

operator>=() [27/37]

template<typename Coeff >

bool carl::operator>= ( const Term< Coeff > &  lhs, const Monomial::Arg &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 516 of file Term.h.

operator>=() [28/37]

template<typename Coeff >

bool carl::operator>= ( const Term< Coeff > &  lhs, const Term< Coeff > &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 512 of file Term.h.

operator>=() [29/37]

template<typename Coeff >

bool carl::operator>= ( const Term< Coeff > &  lhs, Variable  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 520 of file Term.h.

operator>=() [30/37]

template<typename N >

bool carl::operator>=	(	const ThomEncoding< N > &	lhs,
		const N &	rhs
	)

Definition at line 579 of file ThomEncoding.h.

operator>=() [31/37]

template<typename N >

bool carl::operator>=	(	const ThomEncoding< N > &	lhs,
		const ThomEncoding< N > &	rhs
	)

Definition at line 565 of file ThomEncoding.h.

operator>=() [32/37]

template<typename P >

bool carl::operator>= ( const typename FactorizedPolynomial< P >::CoeffType &  _lhs, const FactorizedPolynomial< P > &  _rhs  )

inline

Checks if the first arguments is greater or equal than the second.

Parameters

_lhs	First argument.
_rhs	Second argument.

Returns

_lhs >= _rhs

Definition at line 935 of file FactorizedPolynomial.h.

operator>=() [33/37]

template<typename C , typename O , typename P >

bool carl::operator>= ( const UnivariatePolynomial< C > &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first argument is greater or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs >= rhs

Definition at line 415 of file MultivariatePolynomial_operators.h.

operator>=() [34/37]

template<typename C , typename O , typename P >

bool carl::operator>= ( const UnivariatePolynomial< MultivariatePolynomial< C >> &  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first argument is greater or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs >= rhs

Definition at line 423 of file MultivariatePolynomial_operators.h.

operator>=() [35/37]

bool carl::operator>= ( Variable  lhs, const Monomial::Arg &  rhs  )

inline

Compares two arguments where one is a Monomial and the other is either a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 593 of file Monomial.h.

operator>=() [36/37]

template<typename C , typename O , typename P >

bool carl::operator>= ( Variable  lhs, const MultivariatePolynomial< C, O, P > &  rhs  )

inline

Checks if the first argument is greater or equal than the second.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs >= rhs

Definition at line 406 of file MultivariatePolynomial_operators.h.

operator>=() [37/37]

template<typename Coeff >

bool carl::operator>= ( Variable  lhs, const Term< Coeff > &  rhs  )

inline

Compares two arguments where one is a term and the other is either a term, a monomial or a variable.

Parameters

lhs	First argument.
rhs	Second argument.

Returns

lhs ~ rhs, ~ being the relation that is checked.

Definition at line 532 of file Term.h.

operator>>()

BVValue carl::operator>> ( const BVValue &  lhs, const BVValue &  rhs  )

inline

Definition at line 198 of file BVValue.h.

Here is the call graph for this function:

operator^()

BVValue carl::operator^ ( const BVValue &  lhs, const BVValue &  rhs  )

inline

Definition at line 189 of file BVValue.h.

Here is the call graph for this function:

operator|() [1/2]

BitVector carl::operator|	(	const BitVector &	lhs,
		const BitVector &	rhs
	)

Definition at line 6 of file BitVector.cpp.

operator|() [2/2]

BVValue carl::operator| ( const BVValue &  lhs, const BVValue &  rhs  )

inline

Definition at line 184 of file BVValue.h.

Here is the call graph for this function:

operator~()

BVValue carl::operator~ ( const BVValue &  val )

inline

Definition at line 155 of file BVValue.h.

Here is the call graph for this function:

overloaded()

template<class... Ts>

carl::overloaded

(

Ts...

)

-> overloaded< Ts... >

parse()

template<typename T >

T carl::parse ( const std::string &  n )

inline

Here is the caller graph for this function:

parse< cln::cl_I >()

template<>

cln::cl_I carl::parse< cln::cl_I >

(

const std::string &

n

)

parse< cln::cl_RA >()

template<>

cln::cl_RA carl::parse< cln::cl_RA >

(

const std::string &

n

)

parse< mpq_class >()

template<>

mpq_class carl::parse< mpq_class >

(

const std::string &

n

)

Definition at line 163 of file operations.cpp.

Here is the call graph for this function:

parse< mpz_class >()

template<>

mpz_class carl::parse< mpz_class >

(

const std::string &

n

)

Definition at line 150 of file operations.cpp.

Here is the call graph for this function:

pow() [1/14]

template<>

cln::cl_RA carl::pow ( const cln::cl_RA &  basis, std::size_t  exp  )

inline

Calculate the power of some fraction to some positive integer.

Parameters

basis	Basis.
exp	Exponent.

Returns

Definition at line 386 of file operations.h.

Here is the call graph for this function:

pow() [2/14]

template<typename FloatType >

FLOAT_T<FloatType> carl::pow ( const FLOAT_T< FloatType > &  _in, size_t  _exp  )

inline

Definition at line 1452 of file FLOAT_T.h.

Here is the call graph for this function:

Here is the caller graph for this function:

pow() [3/14]

template<typename Number , typename Integer >

Interval<Number> carl::pow	(	const Interval< Number > &	i,
		Integer	exp
	)

Definition at line 11 of file Power.h.

Here is the call graph for this function:

Here is the caller graph for this function:

pow() [4/14]

Monomial::Arg carl::pow ( const Monomial &  m, uint  exp  )

inline

Calculates the given power of a monomial m.

Parameters

m	The monomial.
exp	Exponent.

Returns

m to the power of exp.

Definition at line 14 of file Power.h.

Here is the call graph for this function:

pow() [5/14]

Monomial::Arg carl::pow ( const Monomial::Arg &  m, uint  exp  )

inline

Definition at line 26 of file Power.h.

Here is the call graph for this function:

pow() [6/14]

template<>

mpq_class carl::pow ( const mpq_class &  basis, std::size_t  exp  )

inline

Definition at line 386 of file operations.h.

Here is the call graph for this function:

pow() [7/14]

template<>

mpz_class carl::pow ( const mpz_class &  basis, std::size_t  exp  )

inline

Definition at line 379 of file operations.h.

Here is the call graph for this function:

pow() [8/14]

template<typename C , typename O , typename P >

MultivariatePolynomial<C,O,P> carl::pow	(	const MultivariatePolynomial< C, O, P > &	p,
		std::size_t	exp
	)

Definition at line 41 of file Power.h.

Here is the call graph for this function:

pow() [9/14]

template<typename T , DisableIf< is_interval_type< T >> = dummy>

T carl::pow	(	const T &	basis,
		std::size_t	exp
	)

Implements a fast exponentiation on an arbitrary type T.

To use carl::pow() on a type T, the following must be defined:

• carl::constant_one<T>,
• T::operator=(const T&) and
• operator*(const T&, const T&). Alternatively, carl::pow() can be specialized for T explicitly.

  Parameters

  basis	A number.
  exp	The exponent.

  Returns

  basis to the power of exp.

Definition at line 61 of file operations_generic.h.

Here is the call graph for this function:

pow() [10/14]

template<typename Coeff >

Term<Coeff> carl::pow	(	const Term< Coeff > &	t,
		uint	exp
	)

Definition at line 32 of file Power.h.

Here is the call graph for this function:

pow() [11/14]

template<typename Coeff >

UnivariatePolynomial<Coeff> carl::pow	(	const UnivariatePolynomial< Coeff > &	p,
		std::size_t	exp
	)

Returns a polynomial to the given power.

Parameters

p	The polynomial.
exp	Exponent.

Returns

The polynomial to the power of exp.

Definition at line 77 of file Power.h.

Here is the call graph for this function:

Here is the caller graph for this function:

pow() [12/14]

double carl::pow ( double  in, uint  exp  )

inline

Definition at line 173 of file operations.h.

Here is the call graph for this function:

pow() [13/14]

template<typename Pol , bool AS>

RationalFunction<Pol, AS> carl::pow	(	unsigned	exp,
		const RationalFunction< Pol, AS > &	rf
	)

Definition at line 555 of file RationalFunction.h.

Here is the call graph for this function:

pow() [14/14]

Monomial::Arg carl::pow	(	Variable	v,
		std::size_t	exp
	)

Definition at line 353 of file Monomial.cpp.

Here is the call graph for this function:

pow_assign() [1/2]

template<typename Number , typename Integer >

void carl::pow_assign	(	Interval< Number > &	i,
		Integer	exp
	)

Definition at line 46 of file Power.h.

Here is the call graph for this function:

pow_assign() [2/2]

template<typename T >

void carl::pow_assign	(	T &	t,
		std::size_t	exp
	)

Implements a fast exponentiation on an arbitrary type T.

The result is stored in the given number. To use carl::pow_assign() on a type T, the following must be defined:

• carl::constant_one<T>,
• T::operator=(const T&) and
• operator*(const T&, const T&). Alternatively, carl::pow() can be specialized for T explicitly.

  Parameters

  t	A number.
  exp	The exponent.

Definition at line 85 of file operations_generic.h.

Here is the call graph for this function:

pow_naive()

template<typename C , typename O , typename P >

MultivariatePolynomial<C,O,P> carl::pow_naive	(	const MultivariatePolynomial< C, O, P > &	p,
		std::size_t	exp
	)

Definition at line 57 of file Power.h.

Here is the call graph for this function:

primitive_euclidean()

template<typename Coeff >

UnivariatePolynomial<Coeff> carl::primitive_euclidean	(	const UnivariatePolynomial< Coeff > &	a,
		const UnivariatePolynomial< Coeff > &	b
	)

Computes the GCD of two univariate polynomial with coefficients from a unique factorization domain using the primitive euclidean algorithm.

See also

[3], page 57, Algorithm 2.3

Definition at line 16 of file PrimitiveEuclidean.h.

Here is the call graph for this function:

Here is the caller graph for this function:

primitive_part()

template<typename Coeff >

UnivariatePolynomial<Coeff> carl::primitive_part

(

const UnivariatePolynomial< Coeff > &

p

)

The primitive part of p is the normal part of p divided by the content of p.

The primitive part of zero is zero.

See also

[3], page 53, definition 2.18

Returns

The primitive part of the polynomial.

Definition at line 19 of file PrimitivePart.h.

Here is the call graph for this function:

Here is the caller graph for this function:

principalSubresultantsCoefficients()

template<typename Coeff >

std::vector<UnivariatePolynomial<Coeff> > carl::principalSubresultantsCoefficients	(	const UnivariatePolynomial< Coeff > &	p,
		const UnivariatePolynomial< Coeff > &	q,
		SubresultantStrategy	strategy = SubresultantStrategy::Default
	)

Definition at line 273 of file Resultant.h.

Here is the call graph for this function:

printMatrix()

template<typename Coeff >

void carl::printMatrix

(

const CoeffMatrix< Coeff > &

m

)

Definition at line 40 of file CharPol.h.

printStacktrace()

void carl::printStacktrace

(

)

Uses GDB to print a stack trace.

Definition at line 23 of file debug.cpp.

pseudo_primitive_part()

template<typename Coeff >

UnivariatePolynomial<Coeff> carl::pseudo_primitive_part

(

const UnivariatePolynomial< Coeff > &

p

)

Returns this/divisor where divisor is the numeric content of this polynomial.

Returns

Definition at line 36 of file PrimitivePart.h.

Here is the call graph for this function:

pseudo_remainder() [1/2]

template<typename C , typename O , typename P >

MultivariatePolynomial<C,O,P> carl::pseudo_remainder	(	const MultivariatePolynomial< C, O, P > &	dividend,
		const MultivariatePolynomial< C, O, P > &	divisor,
		Variable	var
	)

Definition at line 217 of file Remainder.h.

Here is the call graph for this function:

pseudo_remainder() [2/2]

template<typename Coeff >

UnivariatePolynomial<Coeff> carl::pseudo_remainder	(	const UnivariatePolynomial< Coeff > &	dividend,
		const UnivariatePolynomial< Coeff > &	divisor
	)

Calculates the pseudo-remainder.

See also

[3], page 55, Pseudo-Division Property

Definition at line 105 of file Remainder.h.

Here is the call graph for this function:

Here is the caller graph for this function:

quotient() [1/9]

cln::cl_I carl::quotient ( const cln::cl_I &  a, const cln::cl_I &  b  )

inline

Divide two integers.

Discards the remainder of the division.

Parameters

a	First argument.
b	Second argument.

Returns

.

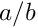Definition at line 514 of file operations.h.

quotient() [2/9]

cln::cl_RA carl::quotient ( const cln::cl_RA &  a, const cln::cl_RA &  b  )

inline

Divide two fractions.

Parameters

a	First argument.
b	Second argument.

Returns

.

Definition at line 503 of file operations.h.

quotient() [3/9]

template<typename FloatType >

FLOAT_T<FloatType> carl::quotient ( const FLOAT_T< FloatType > &  _lhs, const FLOAT_T< FloatType > &  _rhs  )

inline

Implements the division with remainder.

Parameters

_lhs
_rhs

Returns

Number which holds the result.

Definition at line 1380 of file FLOAT_T.h.

quotient() [4/9]

template<typename IntegerT >

GFNumber<IntegerT> carl::quotient	(	const GFNumber< IntegerT > &	lhs,
		const GFNumber< IntegerT > &	rhs
	)

Definition at line 185 of file GFNumber.h.

quotient() [5/9]

template<typename Number >

Interval<Number> carl::quotient ( const Interval< Number > &  _lhs, const Interval< Number > &  _rhs  )

inline

Implements the division with remainder.

Parameters

_lhs
_rhs

Returns

Interval which holds the result.

Definition at line 1488 of file Interval.h.

Here is the call graph for this function:

Here is the caller graph for this function:

quotient() [6/9]

mpq_class carl::quotient ( const mpq_class &  n, const mpq_class &  d  )

inline

Definition at line 457 of file operations.h.

quotient() [7/9]

mpz_class carl::quotient ( const mpz_class &  n, const mpz_class &  d  )

inline

Definition at line 443 of file operations.h.

Here is the call graph for this function:

quotient() [8/9]

template<typename C , typename O , typename P >

MultivariatePolynomial<C,O,P> carl::quotient	(	const MultivariatePolynomial< C, O, P > &	dividend,
		const MultivariatePolynomial< C, O, P > &	divisor
	)

Calculates the quotient of a polynomial division.

Definition at line 14 of file Quotient.h.

Here is the call graph for this function:

quotient() [9/9]

sint carl::quotient ( sint  n, sint  m  )

inline

Definition at line 145 of file operations.h.

rationalize() [1/6]

template<typename T >

T carl::rationalize ( const PreventConversion< mpq_class > &  )

inline

rationalize() [2/6]

template<>

double carl::rationalize ( double  n )

inline

Definition at line 98 of file operations.h.

Here is the caller graph for this function:

rationalize() [3/6]

template<typename T >

T carl::rationalize ( float  n )

inline

rationalize() [4/6]

template<typename T >

T carl::rationalize ( int  n )

inline

rationalize() [5/6]

template<typename T >

T carl::rationalize ( sint  n )

inline

rationalize() [6/6]

template<typename T >

T carl::rationalize ( uint  n )

inline

rationalize< cln::cl_RA >() [1/5]

template<>

cln::cl_RA carl::rationalize< cln::cl_RA >

(

double

n

)

rationalize< cln::cl_RA >() [2/5]

template<>

cln::cl_RA carl::rationalize< cln::cl_RA >

(

float

n

)

rationalize< cln::cl_RA >() [3/5]

template<>

cln::cl_RA carl::rationalize< cln::cl_RA > ( int  n )

inline

Definition at line 206 of file operations.h.

rationalize< cln::cl_RA >() [4/5]

template<>

cln::cl_RA carl::rationalize< cln::cl_RA > ( sint  n )

inline

Definition at line 216 of file operations.h.

rationalize< cln::cl_RA >() [5/5]

template<>

cln::cl_RA carl::rationalize< cln::cl_RA > ( uint  n )

inline

Definition at line 211 of file operations.h.

rationalize< FLOAT_T< double > >()

template<>

FLOAT_T<double> carl::rationalize< FLOAT_T< double > > ( double  n )

inline

Definition at line 1520 of file FLOAT_T.h.

rationalize< FLOAT_T< float > >()

template<>

FLOAT_T<float> carl::rationalize< FLOAT_T< float > > ( float  n )

inline

Definition at line 1520 of file FLOAT_T.h.

rationalize< FLOAT_T< mpq_class > >()

template<>

FLOAT_T<mpq_class> carl::rationalize< FLOAT_T< mpq_class > > ( double  n )

inline

Definition at line 1520 of file FLOAT_T.h.

rationalize< mpq_class >() [1/6]

template<>

mpq_class carl::rationalize< mpq_class > ( const PreventConversion< mpq_class > &  n )

inline

Definition at line 230 of file operations.h.

rationalize< mpq_class >() [2/6]

template<>

mpq_class carl::rationalize< mpq_class > ( double  n )

inline

Definition at line 209 of file operations.h.

rationalize< mpq_class >() [3/6]

template<>

mpq_class carl::rationalize< mpq_class > ( float  n )

inline

Definition at line 203 of file operations.h.

Here is the caller graph for this function:

rationalize< mpq_class >() [4/6]

template<>

mpq_class carl::rationalize< mpq_class > ( int  n )

inline

Definition at line 215 of file operations.h.

rationalize< mpq_class >() [5/6]

template<>

mpq_class carl::rationalize< mpq_class > ( sint  n )

inline

Definition at line 225 of file operations.h.

rationalize< mpq_class >() [6/6]

template<>

mpq_class carl::rationalize< mpq_class > ( uint  n )

inline

Definition at line 220 of file operations.h.

real_roots() [1/3]

template<typename Coeff , typename Ordering , typename Policies >

auto carl::real_roots	(	const ContextPolynomial< Coeff, Ordering, Policies > &	p,
		const Assignment< typename ContextPolynomial< Coeff, Ordering, Policies >::RootType > &	a
	)

Definition at line 151 of file RealRoots.h.

Here is the call graph for this function:

real_roots() [2/3]

template<typename Coeff , typename Number >

RealRootsResult<IntRepRealAlgebraicNumber<Number> > carl::real_roots	(	const UnivariatePolynomial< Coeff > &	poly,
		const Assignment< IntRepRealAlgebraicNumber< Number >> &	varToRANMap,
		const Interval< Number > &	interval = Interval<Number>::unbounded_interval()
	)

Replace all variables except one of the multivariate polynomial 'p' by numbers as given in the mapping 'm', which creates a univariate polynomial, and return all roots of that created polynomial.

Note that 'p' is represented as a univariate polynomial with polynomial coefficients. Its main variable is not replaced and stays the main variable of the created polynomial. However, all variables in the polynomial coefficients are replaced, which is why

• the main variable of 'p' must not be in 'm'
• all variables from the coefficients of 'p' must be in 'm'

The roots are sorted in ascending order. Returns a RealRootsResult indicating whether the roots could be isolated or the polynomial was not univariate or is nullified.

Definition at line 69 of file RealRoots.h.

Here is the call graph for this function:

real_roots() [3/3]

template<typename Coeff , typename Number = typename UnderlyingNumberType<Coeff>::type, EnableIf< std::is_same< Coeff, Number >> = dummy>

RealRootsResult<IntRepRealAlgebraicNumber<Number> > carl::real_roots	(	const UnivariatePolynomial< Coeff > &	polynomial,
		const Interval< Number > &	interval = Interval<Number>::unbounded_interval()
	)

Find all real roots of a univariate 'polynomial' with numeric coefficients within a given 'interval'.

Find all real roots of a univariate 'polynomial' with non-numeric coefficients within a given 'interval'.

The roots are sorted in ascending order.

However, all coefficients must be types that contain numeric numbers that are retrievable by using .constant_part(); The roots are sorted in ascending order.

Definition at line 25 of file RealRoots.h.

Here is the call graph for this function:

Here is the caller graph for this function:

real_variables()

template<typename T >

carlVariables carl::real_variables ( const T &  t )

inline

Definition at line 240 of file Variables.h.

Here is the call graph for this function:

realRootsThom() [1/3]

template<typename Number >

std::list<ThomEncoding<Number> > carl::realRootsThom	(	const MultivariatePolynomial< Number > &	p,
		Variable::Arg	mainVar,
		const std::map< Variable, ThomEncoding< Number >> &	m = {},
		const Interval< Number > &	interval = Interval<Number>::unbounded_interval()
	)

Definition at line 36 of file ThomRootFinder.h.

realRootsThom() [2/3]

template<typename Number >

std::list< ThomEncoding< Number > > carl::realRootsThom	(	const MultivariatePolynomial< Number > &	p,
		Variable::Arg	mainVar,
		std::shared_ptr< ThomEncoding< Number >>	point_ptr,
		const Interval< Number > &	interval = Interval<Number>::unbounded_interval()
	)

Definition at line 117 of file ThomRootFinder.h.

Here is the call graph for this function:

Here is the caller graph for this function:

realRootsThom() [3/3]

template<typename Coeff , typename Number >

std::list<RealAlgebraicNumber<Number> > carl::realRootsThom	(	const UnivariatePolynomial< Coeff > &	p,
		const std::map< Variable, RealAlgebraicNumber< Number >> &	m,
		const Interval< Number > &	interval
	)

Definition at line 269 of file ThomRootFinder.h.

Here is the call graph for this function:

reciprocal() [1/2]

cln::cl_RA carl::reciprocal ( const cln::cl_RA &  a )

inline

Definition at line 546 of file operations.h.

Here is the caller graph for this function:

reciprocal() [2/2]

mpq_class carl::reciprocal ( const mpq_class &  a )

inline

Definition at line 520 of file operations.h.

relationIsSigned()

bool carl::relationIsSigned ( BVCompareRelation  _r )

inline

Definition at line 84 of file BVCompareRelation.h.

relationIsStrict()

bool carl::relationIsStrict ( BVCompareRelation  _r )

inline

Definition at line 75 of file BVCompareRelation.h.

remainder() [1/6]

cln::cl_I carl::remainder ( const cln::cl_I &  a, const cln::cl_I &  b  )

inline

Calculate the remainder of the integer division.

Parameters

a	First argument.
b	Second argument.

Returns

.

Definition at line 526 of file operations.h.

Here is the caller graph for this function:

remainder() [2/6]

mpz_class carl::remainder ( const mpz_class &  n, const mpz_class &  m  )

inline

Definition at line 439 of file operations.h.

Here is the call graph for this function:

remainder() [3/6]

template<typename C , typename O , typename P >

MultivariatePolynomial<C,O,P> carl::remainder	(	const MultivariatePolynomial< C, O, P > &	dividend,
		const MultivariatePolynomial< C, O, P > &	divisor
	)

Definition at line 173 of file Remainder.h.

Here is the call graph for this function:

remainder() [4/6]

template<typename Coeff >

UnivariatePolynomial<Coeff> carl::remainder	(	const UnivariatePolynomial< Coeff > &	dividend,
		const UnivariatePolynomial< Coeff > &	divisor
	)

Definition at line 95 of file Remainder.h.

Here is the call graph for this function:

remainder() [5/6]

template<typename Coeff >

UnivariatePolynomial<Coeff> carl::remainder	(	const UnivariatePolynomial< Coeff > &	dividend,
		const UnivariatePolynomial< Coeff > &	divisor,
		const Coeff &	prefactor
	)

Definition at line 90 of file Remainder.h.

Here is the call graph for this function:

remainder() [6/6]

sint carl::remainder ( sint  n, sint  m  )

inline

Definition at line 138 of file operations.h.

remainder_helper()

template<typename Coeff >

UnivariatePolynomial<Coeff> carl::remainder_helper	(	const UnivariatePolynomial< Coeff > &	dividend,
		const UnivariatePolynomial< Coeff > &	divisor,
		const Coeff *	prefactor = nullptr
	)

Does the heavy lifting for the remainder computation of polynomial division.

Parameters

divisor
prefactor

See also

[3], page 55, Pseudo-Division Property

Returns

Definition at line 20 of file Remainder.h.

Here is the call graph for this function:

Here is the caller graph for this function:

replace_main_variable()

template<typename Coeff >

UnivariatePolynomial<Coeff> carl::replace_main_variable	(	const UnivariatePolynomial< Coeff > &	p,
		Variable	newVar
	)

Replaces the main variable in a polynomial.

Parameters

p	The polynomial.
newVar	New main variable.

Returns

New polynomial.

Definition at line 31 of file Representation.h.

Here is the call graph for this function:

Here is the caller graph for this function:

representingFormula()

template<typename Rational , typename Poly >

Formula<Poly> carl::representingFormula	(	const ModelVariable &	mv,
		const Model< Rational, Poly > &	model
	)

resolve_negation()

template<typename Pol >

Formula<Pol> carl::resolve_negation	(	const Formula< Pol > &	f,
		bool	_keepConstraint = true,
		bool	resolve_varcomp = false
	)

Resolves the outermost negation of this formula.

Parameters

_keepConstraint

A flag indicating whether to change constraints in order to resolve the negation in front of them, or to keep the constraints and leave the negation.

Definition at line 12 of file Negations.h.

Here is the call graph for this function:

Here is the caller graph for this function:

resultant() [1/2]

template<typename Coeff , typename Ordering , typename Policies >

auto carl::resultant ( const ContextPolynomial< Coeff, Ordering, Policies > &  p, const ContextPolynomial< Coeff, Ordering, Policies > &  q  )

inline

Definition at line 22 of file Functions.h.

Here is the call graph for this function:

Here is the caller graph for this function:

resultant() [2/2]

template<typename Coeff >

UnivariatePolynomial<Coeff> carl::resultant	(	const UnivariatePolynomial< Coeff > &	p,
		const UnivariatePolynomial< Coeff > &	q,
		SubresultantStrategy	strategy = SubresultantStrategy::Default
	)

Definition at line 289 of file Resultant.h.

Here is the call graph for this function:

returnFalse()

template<typename T >

bool carl::returnFalse	(	const T &	,
		const T &
	)

Definition at line 41 of file Cache.h.

root_safe() [1/2]

std::pair<cln::cl_RA, cln::cl_RA> carl::root_safe	(	const cln::cl_RA &	a,
		uint	n
	)

Here is the caller graph for this function:

root_safe() [2/2]

std::pair< mpq_class, mpq_class > carl::root_safe	(	const mpq_class &	a,
		uint	n
	)

Calculate the nth root of a fraction.

The precise result is contained in the resulting interval.

Definition at line 72 of file operations.cpp.

round() [1/4]

cln::cl_I carl::round ( const cln::cl_I &  n )

inline

Round an integer to next integer, that is do nothing.

Parameters

n	An integer.

Returns

The next integer.

Definition at line 264 of file operations.h.

round() [2/4]

cln::cl_I carl::round ( const cln::cl_RA &  n )

inline

Round a fraction to next integer.

Parameters

n	A fraction.

Returns

The next integer.

Definition at line 255 of file operations.h.

Here is the caller graph for this function:

round() [3/4]

mpz_class carl::round ( const mpq_class &  n )

inline

Definition at line 264 of file operations.h.

Here is the call graph for this function:

round() [4/4]

mpz_class carl::round ( const mpz_class &  n )

inline

Definition at line 274 of file operations.h.

roundDown()

template<typename Rational >

double carl::roundDown	(	const Rational &	o,
		bool	overapproximate = false
	)

Returns a down-rounded representation of the given numeric.

Parameters

o	Number to round.
overapproximate	Flag if overapproximation shall be guaranteed.

Returns

Double representation of o.

Definition at line 12 of file generic.h.

Here is the call graph for this function:

Here is the caller graph for this function:

roundUp()

template<typename Rational >

double carl::roundUp	(	const Rational &	o,
		bool	overapproximate = false
	)

Returns a up-rounded representation of the given numeric.

Parameters

o
overapproximate

Returns

double representation of o (overapprox) Note, that it can return the double INFINITY.

Definition at line 38 of file generic.h.

Here is the call graph for this function:

Here is the caller graph for this function:

sample()

template<typename Number >

Number carl::sample	(	const Interval< Number > &	i,
		bool	includingBounds = true
	)

Searches for some point in this interval, preferably near the midpoint and with a small representation.

Checks the integers next to the midpoint, uses the midpoint if both are outside.

Returns

Some point within this interval.

Definition at line 30 of file Sampling.h.

Here is the call graph for this function:

Here is the caller graph for this function:

sample_above() [1/3]

template<typename Number >

Number carl::sample_above

(

const IntRepRealAlgebraicNumber< Number > &

n

)

Definition at line 246 of file Ran.h.

Here is the call graph for this function:

sample_above() [2/3]

template<typename Number , typename = std::enable_if_t<is_number_type<Number>::value>>

Number carl::sample_above

(

const Number &

n

)

Definition at line 18 of file NumberOperations.h.

Here is the call graph for this function:

sample_above() [3/3]

template<typename Number >

RealAlgebraicNumberThom<Number> carl::sample_above

(

const RealAlgebraicNumberThom< Number > &

n

)

Definition at line 149 of file ran_thom.h.

sample_below() [1/3]

template<typename Number >

Number carl::sample_below

(

const IntRepRealAlgebraicNumber< Number > &

n

)

Definition at line 250 of file Ran.h.

Here is the call graph for this function:

sample_below() [2/3]

template<typename Number , typename = std::enable_if_t<is_number_type<Number>::value>>

Number carl::sample_below

(

const Number &

n

)

Definition at line 22 of file NumberOperations.h.

Here is the call graph for this function:

sample_below() [3/3]

template<typename Number >

RealAlgebraicNumberThom<Number> carl::sample_below

(

const RealAlgebraicNumberThom< Number > &

n

)

Definition at line 153 of file ran_thom.h.

sample_between() [1/7]

template<typename Number >

Number carl::sample_between	(	const IntRepRealAlgebraicNumber< Number > &	lower,
		const IntRepRealAlgebraicNumber< Number > &	upper
	)

Definition at line 254 of file Ran.h.

Here is the call graph for this function:

sample_between() [2/7]

template<typename Number >

Number carl::sample_between	(	const IntRepRealAlgebraicNumber< Number > &	lower,
		const Number &	upper
	)

Definition at line 267 of file Ran.h.

Here is the call graph for this function:

sample_between() [3/7]

template<typename Number >

Number carl::sample_between	(	const Number &	lower,
		const IntRepRealAlgebraicNumber< Number > &	upper
	)

Definition at line 280 of file Ran.h.

Here is the call graph for this function:

sample_between() [4/7]

template<typename Number , typename = std::enable_if_t<is_number_type<Number>::value>>

Number carl::sample_between	(	const Number &	lower,
		const Number &	upper
	)

Definition at line 26 of file NumberOperations.h.

Here is the call graph for this function:

Here is the caller graph for this function:

sample_between() [5/7]

template<typename Number >

Number carl::sample_between	(	const Number &	lower,
		const RealAlgebraicNumberThom< Number > &	upper
	)

Definition at line 165 of file ran_thom.h.

sample_between() [6/7]

template<typename Number >

Number carl::sample_between	(	const RealAlgebraicNumberThom< Number > &	lower,
		const Number &	upper
	)

Definition at line 161 of file ran_thom.h.

sample_between() [7/7]

template<typename Number >

RealAlgebraicNumberThom<Number> carl::sample_between	(	const RealAlgebraicNumberThom< Number > &	lower,
		const RealAlgebraicNumberThom< Number > &	upper
	)

Definition at line 157 of file ran_thom.h.

sample_infty()

template<typename Number >

Number carl::sample_infty

(

const Interval< Number > &

i

)

Searches for some point in this interval, preferably far aways from zero and with a small representation.

Checks the integer next to the right endpoint if the interval is semi-positive. Checks the integer next to the left endpoint if the interval is semi-negative. Uses zero otherwise.

Returns

Some point within this interval.

Definition at line 129 of file Sampling.h.

Here is the call graph for this function:

sample_left()

template<typename Number >

Number carl::sample_left

(

const Interval< Number > &

i

)

Searches for some point in this interval, preferably near the left endpoint and with a small representation.

Checks the integer next to the left endpoint, uses the midpoint if it is outside.

Returns

Some point within this interval.

Definition at line 83 of file Sampling.h.

Here is the call graph for this function:

Here is the caller graph for this function:

sample_right()

template<typename Number >

Number carl::sample_right

(

const Interval< Number > &

i

)

Searches for some point in this interval, preferably near the right endpoint and with a small representation.

Checks the integer next to the right endpoint, uses the midpoint if it is outside.

Returns

Some point within this interval.

Definition at line 98 of file Sampling.h.

Here is the call graph for this function:

Here is the caller graph for this function:

sample_stern_brocot()

template<typename Number >

Number carl::sample_stern_brocot	(	const Interval< Number > &	i,
		bool	includingBounds = true
	)

Searches for some point in this interval, preferably near the midpoint and with a small representation.

Uses a binary search based on the Stern-Brocot tree starting from the integer below the midpoint.

Returns

Some point within this interval.

Definition at line 49 of file Sampling.h.

Here is the call graph for this function:

sample_zero()

template<typename Number >

Number carl::sample_zero

(

const Interval< Number > &

i

)

Searches for some point in this interval, preferably near zero and with a small representation.

Checks the integer next to the left endpoint if the interval is semi-positive. Checks the integer next to the right endpoint if the interval is semi-negative. Uses zero otherwise.

Returns

Some point within this interval.

Definition at line 115 of file Sampling.h.

Here is the call graph for this function:

satisfied_by() [1/3]

template<typename Pol >

unsigned carl::satisfied_by	(	const BasicConstraint< Pol > &	c,
		const Assignment< typename Pol::NumberType > &	_assignment
	)

Checks whether the given assignment satisfies this constraint.

Parameters

_assignment

The assignment.

Returns

1, if the given assignment satisfies this constraint. 0, if the given assignment contradicts this constraint. 2, otherwise (possibly not defined for all variables in the constraint, even then it could be possible to obtain the first two results.)

Definition at line 24 of file Evaluation.h.

Here is the call graph for this function:

Here is the caller graph for this function:

satisfied_by() [2/3]

template<typename Pol >

auto carl::satisfied_by	(	const Constraint< Pol > &	c,
		const Assignment< typename Pol::NumberType > &	a
	)

Definition at line 344 of file Constraint.h.

Here is the call graph for this function:

satisfied_by() [3/3]

template<typename T , typename Rational , typename Poly >

unsigned carl::satisfied_by	(	const T &	t,
		const Model< Rational, Poly > &	m
	)

Definition at line 58 of file ModelEvaluation.h.

Here is the call graph for this function:

satisfies() [1/2]

template<typename Rational , typename Poly >

unsigned carl::satisfies	(	const Model< Rational, Poly > &	_assignment,
		const Formula< Poly > &	_formula
	)

Parameters

_assignment	The assignment for which to check whether the given formula is satisfied by it.
_formula	The formula to be satisfied.

Returns

0, if this formula is violated by the given assignment; 1, if this formula is satisfied by the given assignment; 2, otherwise.

satisfies() [2/2]

template<typename Rational , typename Poly >

unsigned carl::satisfies	(	const Model< Rational, Poly > &	_model,
		const std::map< Variable, Rational > &	_assignment,
		const std::map< BVVariable, BVTerm > &	bvAssigns,
		const Formula< Poly > &	_formula
	)

Parameters

_model	The assignment for which to check whether the given formula is satisfied by it.
_assignment	The map to store the rational assignments in.
bvAssigns	The map to store the bitvector assignments in.
_formula	The formula to be satisfied.

Returns

0, if this formula is violated by the given assignment; 1, if this formula is satisfied by the given assignment; 2, otherwise.

separable_part()

Monomial::Arg carl::separable_part ( const Monomial &  m )

inline

Calculates the separable part of this monomial.

For a monomial with , this is .

Returns

Separable part.

Definition at line 12 of file SeparablePart.h.

Here is the call graph for this function:

Here is the caller graph for this function:

set_complement()

template<typename Number >

bool carl::set_complement	(	const Interval< Number > &	interval,
		Interval< Number > &	resA,
		Interval< Number > &	resB
	)

Calculates the complement in a set-theoretic manner (can result in two distinct intervals).

Parameters

interval	Interval.
resA	Result a.
resB	Result b.

Returns

True, if the result is twofold.

Definition at line 16 of file SetTheory.h.

Here is the call graph for this function:

set_difference()

template<typename Number >

bool carl::set_difference	(	const Interval< Number > &	lhs,
		const Interval< Number > &	rhs,
		Interval< Number > &	resA,
		Interval< Number > &	resB
	)

Calculates the difference of two intervals in a set-theoretic manner: lhs \ rhs (can result in two distinct intervals).

Parameters

lhs	First interval.
rhs	Second interval.
resA	Result a.
resB	Result b.

Returns

True, if the result is twofold.

Definition at line 52 of file SetTheory.h.

Here is the call graph for this function:

Here is the caller graph for this function:

set_have_intersection()

template<typename Number >

bool carl::set_have_intersection	(	const Interval< Number > &	lhs,
		const Interval< Number > &	rhs
	)

Definition at line 118 of file SetTheory.h.

Here is the call graph for this function:

Here is the caller graph for this function:

set_intersection()

template<typename Number >

Interval<Number> carl::set_intersection	(	const Interval< Number > &	lhs,
		const Interval< Number > &	rhs
	)

Intersects two intervals in a set-theoretic manner.

Parameters

lhs	Lefthand side.
rhs	Righthand side.

Returns

Result.

Definition at line 99 of file SetTheory.h.

Here is the call graph for this function:

Here is the caller graph for this function:

set_is_proper_subset()

template<typename Number >

bool carl::set_is_proper_subset	(	const Interval< Number > &	lhs,
		const Interval< Number > &	rhs
	)

Checks whether lhs is a proper subset of rhs.

Definition at line 128 of file SetTheory.h.

Here is the call graph for this function:

set_is_subset()

template<typename Number >

bool carl::set_is_subset	(	const Interval< Number > &	lhs,
		const Interval< Number > &	rhs
	)

Checks whether lhs is a subset of rhs.

Definition at line 143 of file SetTheory.h.

Here is the call graph for this function:

set_symmetric_difference()

template<typename Number >

bool carl::set_symmetric_difference	(	const Interval< Number > &	lhs,
		const Interval< Number > &	rhs,
		Interval< Number > &	resA,
		Interval< Number > &	resB
	)

Calculates the symmetric difference of two intervals in a set-theoretic manner (can result in two distinct intervals).

Parameters

lhs	First interval.
rhs	Second interval.
resA	Result a.
resB	Result b.

Returns

True, if the result is twofold.

Definition at line 162 of file SetTheory.h.

Here is the call graph for this function:

set_union()

template<typename Number >

bool carl::set_union	(	const Interval< Number > &	lhs,
		const Interval< Number > &	rhs,
		Interval< Number > &	resA,
		Interval< Number > &	resB
	)

Computes the union of two intervals (can result in two distinct intervals).

Parameters

lhs	First interval.
rhs	Second interval.
resA	Result a.
resB	Result b.

Returns

True, if the result is twofold.

Definition at line 187 of file SetTheory.h.

Here is the call graph for this function:

Here is the caller graph for this function:

sgn() [1/3]

template<typename Number >

Sign carl::sgn

(

const IntRepRealAlgebraicNumber< Number > &

n

)

Definition at line 341 of file Ran.h.

Here is the call graph for this function:

sgn() [2/3]

template<typename Number >

Sign carl::sgn	(	const IntRepRealAlgebraicNumber< Number > &	n,
		const UnivariatePolynomial< Number > &	p
	)

Definition at line 353 of file Ran.h.

Here is the call graph for this function:

sgn() [3/3]

template<typename Number >

Sign carl::sgn

(

const Number &

n

)

Obtain the sign of the given number.

This method relies on the comparison operators for the type of the given number.

Parameters

n

Number

Returns

Sign of n

Definition at line 54 of file Sign.h.

Here is the caller graph for this function:

sign_variations() [1/3]

template<typename Coefficient >

uint carl::sign_variations	(	const UnivariatePolynomial< Coefficient > &	polynomial,
		const Interval< Coefficient > &	interval
	)

Counts the sign variations (i.e.

an upper bound for the number of real roots) via Descarte's rule of signs. This is an upper bound for countRealRoots().

Parameters

polynomial	A polynomial.
interval	Count roots within this interval.

Returns

Upper bound for number of real roots within the interval.

Definition at line 72 of file SignVariations.h.

Here is the call graph for this function:

sign_variations() [2/3]

template<typename InputIterator >

std::size_t carl::sign_variations	(	InputIterator	begin,
		InputIterator	end
	)

Counts the number of sign variations in the given object range.

The function accepts an range of Sign objects.

Parameters

begin	Start of object range.
end	End of object range.

Returns

Sign variations of objects.

Definition at line 69 of file Sign.h.

Here is the caller graph for this function:

sign_variations() [3/3]

template<typename InputIterator , typename Function >

std::size_t carl::sign_variations	(	InputIterator	begin,
		InputIterator	end,
		const Function &	f
	)

Counts the number of sign variations in the given object range.

The function accepts an object range and an additional function f. If the objects are not of type Sign, the function f can be used to convert the objects to a Sign on the fly. As for the number of sign variations in the evaluations of polynomials p at a position x, this might look like this: signVariations(p.begin(), p.end(), [&x](const Polynomial& p){ return sgn(p.evaluate(x)); });

Parameters

begin	Start of object range.
end	End of object range.
f	Function object to convert objects to Sign.

Returns

Sign variations of objects.

Definition at line 95 of file Sign.h.

signAtMinusInf()

template<typename Number >

Sign carl::signAtMinusInf

(

const UnivariatePolynomial< Number > &

p

)

Definition at line 16 of file UnivariateTarskiQuery.h.

Here is the call graph for this function:

signAtPlusInf()

template<typename Number >

Sign carl::signAtPlusInf

(

const UnivariatePolynomial< Number > &

p

)

Definition at line 27 of file UnivariateTarskiQuery.h.

Here is the call graph for this function:

signed_pseudo_remainder()

template<typename Coeff >

UnivariatePolynomial<Coeff> carl::signed_pseudo_remainder	(	const UnivariatePolynomial< Coeff > &	dividend,
		const UnivariatePolynomial< Coeff > &	divisor
	)

Compute the signed pseudo-remainder.

Definition at line 159 of file Remainder.h.

Here is the call graph for this function:

sin() [1/5]

cln::cl_RA carl::sin ( const cln::cl_RA &  n )

inline

Definition at line 397 of file operations.h.

Here is the call graph for this function:

sin() [2/5]

template<typename FloatType >

FLOAT_T<FloatType> carl::sin ( const FLOAT_T< FloatType > &  _in )

inline

Definition at line 1460 of file FLOAT_T.h.

Here is the call graph for this function:

sin() [3/5]

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

Interval<Number> carl::sin

(

const Interval< Number > &

i

)

Definition at line 10 of file Trigonometry.h.

Here is the call graph for this function:

Here is the caller graph for this function:

sin() [4/5]

mpq_class carl::sin ( const mpq_class &  n )

inline

Definition at line 370 of file operations.h.

Here is the call graph for this function:

sin() [5/5]

double carl::sin ( double  in )

inline

Definition at line 153 of file operations.h.

Here is the caller graph for this function:

sin_assign()

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

void carl::sin_assign

(

Interval< Number > &

i

)

Definition at line 16 of file Trigonometry.h.

Here is the call graph for this function:

sinh()

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

Interval<Number> carl::sinh

(

const Interval< Number > &

i

)

Definition at line 82 of file Trigonometry.h.

Here is the call graph for this function:

Here is the caller graph for this function:

sinh_assign()

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

void carl::sinh_assign

(

Interval< Number > &

i

)

Definition at line 88 of file Trigonometry.h.

Here is the call graph for this function:

solveDiophantine()

template<typename T >

std::vector<T> carl::solveDiophantine

(

MultivariatePolynomial< T > &

p

)

Diophantine Equations solver.

sos_decomposition()

template<typename C , typename O , typename P >

std::vector<std::pair<C,MultivariatePolynomial<C,O,P> > > carl::sos_decomposition	(	const MultivariatePolynomial< C, O, P > &	p,
		bool	not_trivial = false
	)

Definition at line 12 of file SoSDecomposition.h.

Here is the call graph for this function:

Here is the caller graph for this function:

SPolynomial()

template<typename C , typename O , typename P >

MultivariatePolynomial<C,O,P> carl::SPolynomial	(	const MultivariatePolynomial< C, O, P > &	p,
		const MultivariatePolynomial< C, O, P > &	q
	)

Calculates the S-Polynomial of two polynomials.

Definition at line 11 of file SPolynomial.h.

Here is the call graph for this function:

sqrt() [1/5]

cln::cl_RA carl::sqrt

(

const cln::cl_RA &

a

)

sqrt() [2/5]

template<typename FloatType >

FLOAT_T<FloatType> carl::sqrt ( const FLOAT_T< FloatType > &  _in )

inline

Method which returns the square root of the passed number.

Parameters

_in

Number.

Returns

Number which holds the result.

Definition at line 1438 of file FLOAT_T.h.

Here is the call graph for this function:

Here is the caller graph for this function:

sqrt() [3/5]

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

Interval<Number> carl::sqrt

(

const Interval< Number > &

i

)

Definition at line 51 of file Power.h.

Here is the call graph for this function:

Here is the caller graph for this function:

sqrt() [4/5]

mpq_class carl::sqrt

(

const mpq_class &

a

)

Definition at line 34 of file operations.cpp.

Here is the call graph for this function:

sqrt() [5/5]

double carl::sqrt ( double  in )

inline

Definition at line 165 of file operations.h.

Here is the caller graph for this function:

sqrt_assign()

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

void carl::sqrt_assign

(

Interval< Number > &

i

)

Definition at line 71 of file Power.h.

Here is the call graph for this function:

sqrt_exact() [1/2]

bool carl::sqrt_exact	(	const cln::cl_RA &	a,
		cln::cl_RA &	b
	)

Calculate the square root of a fraction if possible.

Parameters

a	The fraction to calculate the square root for.
b	A reference to the rational, in which the result is stored.

Returns

true, if the number to calculate the square root for is a square; false, otherwise.

Here is the caller graph for this function:

sqrt_exact() [2/2]

bool carl::sqrt_exact	(	const mpq_class &	a,
		mpq_class &	b
	)

Calculate the square root of a fraction if possible.

Parameters

a	The fraction to calculate the square root for.
b	A reference to the rational, in which the result is stored.

Returns

true, if the number to calculate the square root for is a square; false, otherwise.

Definition at line 9 of file operations.cpp.

Here is the call graph for this function:

sqrt_fast() [1/2]

std::pair<cln::cl_RA, cln::cl_RA> carl::sqrt_fast

(

const cln::cl_RA &

a

)

Compute square root in a fast but less precise way.

Use cln::sqrt() to obtain an approximation. If the result is rational, i.e. the result is exact, use this result. Otherwise use the nearest integers as bounds on the square root.

Parameters

a	Some number.

Returns

[x,x] if sqrt(a) = x is rational, otherwise [y,z] for y,z integer and y < sqrt(a) < z.

Here is the caller graph for this function:

sqrt_fast() [2/2]

std::pair< mpq_class, mpq_class > carl::sqrt_fast

(

const mpq_class &

a

)

Compute square root in a fast but less precise way.

Use cln::sqrt() to obtain an approximation. If the result is rational, i.e. the result is exact, use this result. Otherwise use the nearest integers as bounds on the square root.

Parameters

a	Some number.

Returns

[x,x] if sqrt(a) = x is rational, otherwise [y,z] for y,z integer and y < sqrt(a) < z.

Definition at line 101 of file operations.cpp.

Here is the call graph for this function:

sqrt_safe() [1/4]

std::pair<cln::cl_RA, cln::cl_RA> carl::sqrt_safe

(

const cln::cl_RA &

a

)

Calculate the square root of a fraction.

If we are able to find a an such that is the exact root of , is returned. If we can not find such a number (note that such a number might not even exist), is returned with . Note that we try to find bounds that are very close to the actual square root. If a small representation is more important than a small interval, sqrt_fast should be used.

Parameters

a	A fraction.

Returns

Interval containing the square root of a.

Here is the caller graph for this function:

sqrt_safe() [2/4]

template<typename FloatType >

std::pair<FLOAT_T<FloatType>, FLOAT_T<FloatType> > carl::sqrt_safe ( const FLOAT_T< FloatType > &  _in )

inline

Definition at line 1446 of file FLOAT_T.h.

Here is the call graph for this function:

sqrt_safe() [3/4]

std::pair< mpq_class, mpq_class > carl::sqrt_safe

(

const mpq_class &

a

)

Definition at line 39 of file operations.cpp.

sqrt_safe() [4/4]

std::pair<double, double> carl::sqrt_safe ( double  in )

inline

Definition at line 169 of file operations.h.

Here is the call graph for this function:

squareFreeFactorization()

template<typename Coeff >

std::map<uint, UnivariatePolynomial<Coeff> > carl::squareFreeFactorization

(

const UnivariatePolynomial< Coeff > &

p

)

Definition at line 15 of file Factorization_univariate.h.

Here is the call graph for this function:

Here is the caller graph for this function:

squareFreePart() [1/2]

template<typename C , typename O , typename P >

MultivariatePolynomial<C,O,P> carl::squareFreePart

(

const MultivariatePolynomial< C, O, P > &

polynomial

)

Definition at line 16 of file SquareFreePart.h.

Here is the call graph for this function:

Here is the caller graph for this function:

squareFreePart() [2/2]

template<typename Coeff , EnableIf< is_subset_of_rationals_type< Coeff >> = dummy>

UnivariatePolynomial<Coeff> carl::squareFreePart

(

const UnivariatePolynomial< Coeff > &

p

)

Definition at line 38 of file SquareFreePart.h.

Here is the call graph for this function:

str2double()

Str2Double_Error carl::str2double ( double &  d, char const *  s  )

inline

Definition at line 62 of file FLOAT_T.h.

stream_joined() [1/2]

template<typename T >

auto carl::stream_joined ( const std::string &  glue, const T &  v  )

inline

Allows to easily output some container with all elements separated by some string.

Usage: os << stream_joined(" ", container).

Parameters

glue	The intermediate string.
v	The container to be printed.

Returns

A temporary object that implements operator<<().

Definition at line 311 of file streamingOperators.h.

Here is the caller graph for this function:

stream_joined() [2/2]

template<typename T , typename F >

auto carl::stream_joined ( const std::string &  glue, const T &  v, F &&  f  )

inline

Allows to easily output some container with all elements separated by some string.

An additional callable f takes care of writing an individual element to the stream. Usage: os << stream_joined(" ", container).

Parameters

glue	The intermediate string.
v	The container to be printed.
f	A callable taking a stream and an element of v.

Returns

A temporary object that implements operator<<().

Definition at line 317 of file streamingOperators.h.

sturm_sequence() [1/2]

template<typename Coeff >

std::vector<UnivariatePolynomial<Coeff> > carl::sturm_sequence

(

const UnivariatePolynomial< Coeff > &

p

)

Computes the sturm sequence of a polynomial as defined at [3], page 333, example 22.

The sturm sequence of p is defined as:

• p_0 = p
• p_1 = p'
• p_k = -rem(p_{k-2}, p_{k-1})

Definition at line 35 of file SturmSequence.h.

Here is the call graph for this function:

sturm_sequence() [2/2]

template<typename Coeff >

std::vector<UnivariatePolynomial<Coeff> > carl::sturm_sequence	(	const UnivariatePolynomial< Coeff > &	p,
		const UnivariatePolynomial< Coeff > &	q
	)

Computes the sturm sequence of two polynomials.

Compared to the regular sturm sequence, we use the second polynomial as p_1.

Definition at line 16 of file SturmSequence.h.

Here is the call graph for this function:

Here is the caller graph for this function:

subresultants()

template<typename Coeff >

std::list<UnivariatePolynomial<Coeff> > carl::subresultants	(	const UnivariatePolynomial< Coeff > &	pol1,
		const UnivariatePolynomial< Coeff > &	pol2,
		SubresultantStrategy	strategy
	)

Implements a subresultants algorithm with optimizations described in [2] .

Parameters

pol1	First polynomial.
pol2	First polynomial.
strategy	Strategy.

Returns

Subresultants of pol1 and pol2.

Case distinction on delta: either we choose b as next subresultant or we could reduce b (delta > 1) and add the reduced version c as next subresultant. The reduction is done by division, which depends on the internal variable order of GiNaC and might fail although for some order it would succeed. In this case, we just do not reduce b. (A relaxed reduction could also be applied.)

After the if-else block, bDeg is the degree of the front-most element of subresultants, be it c or b.

Definition at line 48 of file Resultant.h.

Here is the call graph for this function:

Here is the caller graph for this function:

substitute() [1/20]

template<typename P >

FactorizedPolynomial<P> carl::substitute	(	const FactorizedPolynomial< P > &	p,
		const std::map< Variable, FactorizedPolynomial< P >> &	substitutions
	)

Replace all variables by a value given in their map.

Returns

A new factorized polynomial without the variables in map.

Definition at line 25 of file substitution.h.

Here is the call graph for this function:

substitute() [2/20]

template<typename P >

FactorizedPolynomial<P> carl::substitute	(	const FactorizedPolynomial< P > &	p,
		const std::map< Variable, FactorizedPolynomial< P >> &	substitutions,
		const std::map< Variable, P > &	substitutionsAsP
	)

Replace all variables by a value given in their map.

Returns

A new factorized polynomial without the variables in map.

Definition at line 38 of file substitution.h.

Here is the call graph for this function:

substitute() [3/20]

template<typename P , typename Subs >

FactorizedPolynomial<P> carl::substitute	(	const FactorizedPolynomial< P > &	p,
		const std::map< Variable, Subs > &	substitutions
	)

Replace all variables by a value given in their map.

Returns

A new factorized polynomial without the variables in map.

Definition at line 84 of file substitution.h.

Here is the call graph for this function:

substitute() [4/20]

template<typename P >

FactorizedPolynomial<P> carl::substitute	(	const FactorizedPolynomial< P > &	p,
		Variable	var,
		const FactorizedPolynomial< P > &	value
	)

Replace the given variable by the given value.

Returns

A new factorized polynomial resulting from this substitution.

Definition at line 12 of file substitution.h.

Here is the call graph for this function:

substitute() [5/20]

template<typename Pol , typename Source , typename Target >

Formula<Pol> carl::substitute	(	const Formula< Pol > &	formula,
		const Source &	source,
		const Target &	target
	)

Definition at line 54 of file Substitution.h.

Here is the call graph for this function:

substitute() [6/20]

template<typename Pol >

Formula<Pol> carl::substitute	(	const Formula< Pol > &	formula,
		const std::map< BVVariable, BVTerm > &	replacements
	)

Definition at line 70 of file Substitution.h.

Here is the call graph for this function:

substitute() [7/20]

template<typename Pol >

Formula<Pol> carl::substitute	(	const Formula< Pol > &	formula,
		const std::map< Formula< Pol >, Formula< Pol >> &	replacements
	)

Definition at line 60 of file Substitution.h.

Here is the call graph for this function:

substitute() [8/20]

template<typename Pol >

Formula<Pol> carl::substitute	(	const Formula< Pol > &	formula,
		const std::map< UVariable, UFInstance > &	replacements
	)

Definition at line 75 of file Substitution.h.

Here is the call graph for this function:

substitute() [9/20]

template<typename Pol >

Formula<Pol> carl::substitute	(	const Formula< Pol > &	formula,
		const std::map< Variable, typename Formula< Pol >::PolynomialType > &	replacements
	)

Definition at line 65 of file Substitution.h.

Here is the call graph for this function:

substitute() [10/20]

template<typename Coeff >

Coeff carl::substitute	(	const Monomial &	m,
		const std::map< Variable, Coeff > &	substitutions
	)

Applies the given substitutions to a monomial.

Every variable may be substituted by some value.

Parameters

m	The monomial.
substitutions	Maps variables to numbers.

Returns

Definition at line 19 of file Substitution.h.

Here is the call graph for this function:

Here is the caller graph for this function:

substitute() [11/20]

template<typename C , typename O , typename P >

MultivariatePolynomial<C,O,P> carl::substitute	(	const MultivariatePolynomial< C, O, P > &	p,
		const std::map< Variable, MultivariatePolynomial< C, O, P >> &	substitutions
	)

Definition at line 228 of file Substitution.h.

Here is the call graph for this function:

substitute() [12/20]

template<typename C , typename O , typename P , typename S >

MultivariatePolynomial<C,O,P> carl::substitute	(	const MultivariatePolynomial< C, O, P > &	p,
		const std::map< Variable, S > &	substitutions
	)

Definition at line 193 of file Substitution.h.

Here is the call graph for this function:

substitute() [13/20]

template<typename C , typename O , typename P >

MultivariatePolynomial<C,O,P> carl::substitute	(	const MultivariatePolynomial< C, O, P > &	p,
		const std::map< Variable, Term< C >> &	substitutions
	)

Definition at line 213 of file Substitution.h.

Here is the call graph for this function:

substitute() [14/20]

template<typename C , typename O , typename P >

MultivariatePolynomial<C,O,P> carl::substitute	(	const MultivariatePolynomial< C, O, P > &	p,
		Variable	var,
		const MultivariatePolynomial< C, O, P > &	value
	)

Definition at line 186 of file Substitution.h.

Here is the call graph for this function:

substitute() [15/20]

template<typename Poly >

SqrtEx<Poly> carl::substitute	(	const Poly &	_substituteIn,
		const carl::Variable	_varToSubstitute,
		const SqrtEx< Poly > &	_substituteBy
	)

Substitutes a variable in an expression by a square root expression, which results in a square root expression.

Parameters

_substituteIn	The polynomial to substitute in.
_varToSubstitute	The variable to substitute.
_substituteBy	The square root expression by which the variable gets substituted.

Returns

The resulting square root expression.

Definition at line 34 of file Substitution.h.

Here is the call graph for this function:

substitute() [16/20]

template<typename Poly >

SqrtEx<Poly> carl::substitute	(	const SqrtEx< Poly > &	sqrt_ex,
		const std::map< Variable, typename SqrtEx< Poly >::Rational > &	eval_map
	)

Definition at line 8 of file Substitution.h.

Here is the call graph for this function:

substitute() [17/20]

template<typename T , typename Rational , typename Poly >

T carl::substitute	(	const T &	t,
		const Model< Rational, Poly > &	m
	)

Substitutes a model into an expression t.

The result is always an expression of the same type. This may not be possible for some expressions, for example for uninterpreted equalities.

Definition at line 36 of file ModelEvaluation.h.

Here is the call graph for this function:

substitute() [18/20]

template<typename Coeff >

Term<Coeff> carl::substitute	(	const Term< Coeff > &	t,
		const std::map< Variable, Coeff > &	substitutions
	)

Definition at line 35 of file Substitution.h.

Here is the call graph for this function:

substitute() [19/20]

template<typename Coeff >

Term<Coeff> carl::substitute	(	const Term< Coeff > &	t,
		const std::map< Variable, Term< Coeff >> &	substitutions
	)

Definition at line 55 of file Substitution.h.

Here is the call graph for this function:

substitute() [20/20]

template<typename Coeff >

UnivariatePolynomial<Coeff> carl::substitute	(	const UnivariatePolynomial< Coeff > &	p,
		Variable	var,
		const Coeff &	value
	)

Definition at line 371 of file Substitution.h.

Here is the call graph for this function:

substitute_inplace() [1/11]

template<typename Rational , typename Poly >

void carl::substitute_inplace	(	BVConstraint &	bvc,
		const Model< Rational, Poly > &	m
	)

Substitutes all variables from a model within a bitvector constraint.

Definition at line 37 of file ModelEvaluation_Bitvector.h.

Here is the call graph for this function:

substitute_inplace() [2/11]

template<typename Rational , typename Poly >

void carl::substitute_inplace	(	BVTerm &	bvt,
		const Model< Rational, Poly > &	m
	)

Substitutes all variables from a model within a bitvector term.

Definition at line 13 of file ModelEvaluation_Bitvector.h.

Here is the call graph for this function:

substitute_inplace() [3/11]

template<typename Rational , typename Poly >

void carl::substitute_inplace	(	Constraint< Poly > &	c,
		const Model< Rational, Poly > &	m
	)

Substitutes all variables from a model within a constraint.

May fail to substitute some variables, for example if the values are RANs or SqrtEx.

Definition at line 16 of file ModelEvaluation_Constraint.h.

Here is the call graph for this function:

substitute_inplace() [4/11]

template<typename Rational , typename Poly >

void carl::substitute_inplace	(	Formula< Poly > &	f,
		const Model< Rational, Poly > &	m
	)

Substitutes all variables from a model within a formula.

May fail to substitute some variables, for example if the values are RANs or SqrtEx.

Definition at line 115 of file ModelEvaluation_Formula.h.

Here is the call graph for this function:

substitute_inplace() [5/11]

template<typename C , typename O , typename P >

void carl::substitute_inplace	(	MultivariatePolynomial< C, O, P > &	p,
		Variable	var,
		const MultivariatePolynomial< C, O, P > &	value
	)

Definition at line 64 of file Substitution.h.

Here is the call graph for this function:

substitute_inplace() [6/11]

template<typename Rational >

void carl::substitute_inplace	(	MultivariatePolynomial< Rational > &	p,
		Variable	var,
		const Rational &	r
	)

Substitutes a variable with a rational within a polynomial.

Definition at line 409 of file Substitution.h.

Here is the call graph for this function:

substitute_inplace() [7/11]

template<typename Poly >

void carl::substitute_inplace	(	MultivariateRoot< Poly > &	mr,
		Variable	var,
		const Poly &	poly
	)

Create a copy of the underlying polynomial with the given variable replaced by the given polynomial.

Definition at line 125 of file MultivariateRoot.h.

Here is the call graph for this function:

Here is the caller graph for this function:

substitute_inplace() [8/11]

template<typename Rational , typename Poly >

void carl::substitute_inplace	(	MultivariateRoot< Poly > &	mvr,
		const Model< Rational, Poly > &	m
	)

Substitutes all variables from a model within a MultivariateRoot.

May fail to substitute some variables, for example if the values are RANs or SqrtEx.

Definition at line 13 of file ModelEvaluation_MVRoot.h.

Here is the call graph for this function:

substitute_inplace() [9/11]

template<typename Rational , typename Poly , typename ModelPoly >

void carl::substitute_inplace	(	Poly &	p,
		const Model< Rational, ModelPoly > &	m
	)

Substitutes all variables from a model within a polynomial.

May fail to substitute some variables, for example if the values are RANs or SqrtEx.

Definition at line 16 of file ModelEvaluation_Polynomial.h.

Here is the call graph for this function:

substitute_inplace() [10/11]

template<typename Coeff >

void carl::substitute_inplace	(	UnivariatePolynomial< Coeff > &	p,
		Variable	var,
		const Coeff &	value
	)

Definition at line 348 of file Substitution.h.

Here is the call graph for this function:

substitute_inplace() [11/11]

template<typename Poly , typename Rational >

void carl::substitute_inplace	(	UnivariatePolynomial< Poly > &	p,
		Variable	var,
		const Rational &	r
	)

Definition at line 413 of file Substitution.h.

Here is the call graph for this function:

swap()

void carl::swap ( Variable &  lhs, Variable &  rhs  )

inline

Definition at line 202 of file Variables.h.

Here is the caller graph for this function:

swapConstraintBounds()

template<typename Pol >

bool carl::swapConstraintBounds	(	ConstraintBounds< Pol > &	_constraintBounds,
		Formulas< Pol > &	_intoFormulas,
		bool	_inConjunction
	)

Stores for every polynomial for which we determined bounds for given constraints a minimal set of constraints representing these bounds into the given set of sub-formulas of a conjunction (_inConjunction == true) or disjunction (_inConjunction == false) to construct.

Parameters

_constraintBounds	An object collecting bounds of polynomials.
_intoAsts	A set of sub-formulas of a conjunction (_inConjunction == true) or disjunction (_inConjunction == false) to construct.
_inConjunction	true, if constraints representing the polynomial's bounds are going to be part of a conjunction. false, if constraints representing the polynomial's bounds are going to be part of a disjunction.

Returns

true, if the yet added bounds imply that the conjunction (_inConjunction == true) or disjunction (_inConjunction == false) to which the bounds are added is invalid resp. valid; false, otherwise.

Definition at line 328 of file ConstraintBounds.h.

Here is the caller graph for this function:

switch_main_variable()

template<typename Coeff >

UnivariatePolynomial<MultivariatePolynomial<typename UnderlyingNumberType<Coeff>::type> > carl::switch_main_variable	(	const UnivariatePolynomial< Coeff > &	p,
		Variable	newVar
	)

Switches the main variable using a purely syntactical restructuring.

The resulting polynomial will be algebraicly identical, but have the given variable as its main variable.

Parameters

p	The polynomial.
newVar	New main variable.

Returns

Restructured polynomial.

Definition at line 18 of file Representation.h.

Here is the call graph for this function:

Here is the caller graph for this function:

switch_variable()

template<typename C , typename O , typename P >

MultivariatePolynomial<C,O,P> carl::switch_variable	(	const MultivariatePolynomial< C, O, P > &	p,
		Variable	old_var,
		Variable	new_var
	)

Definition at line 41 of file Representation.h.

Here is the call graph for this function:

tan()

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

Interval<Number> carl::tan

(

const Interval< Number > &

i

)

Definition at line 34 of file Trigonometry.h.

Here is the call graph for this function:

Here is the caller graph for this function:

tan_assign()

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

void carl::tan_assign

(

Interval< Number > &

i

)

Definition at line 40 of file Trigonometry.h.

Here is the call graph for this function:

tanh()

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

Interval<Number> carl::tanh

(

const Interval< Number > &

i

)

Definition at line 106 of file Trigonometry.h.

Here is the call graph for this function:

Here is the caller graph for this function:

tanh_assign()

template<typename Number , EnableIf< std::is_floating_point< Number >> = dummy>

void carl::tanh_assign

(

Interval< Number > &

i

)

Definition at line 112 of file Trigonometry.h.

Here is the call graph for this function:

to_cnf()

template<typename Poly >

Formula<Poly> carl::to_cnf	(	const Formula< Poly > &	f,
		bool	keep_constraints = true,
		bool	simplify_combinations = false,
		bool	tseitin_equivalence = true
	)

Converts the given formula to CNF.

Parameters

f	Formula to convert.
keep_constraints	Indicates whether to keep constraints or allow to change them in resolve_negation().
simplify_combinations	Indicates whether we attempt to simplify combinations of constraints with ConstraintBounds.
tseitin_equivalence	Indicates whether we use implications or equivalences for tseitin variables.

Returns

The formula in CNF.

Definition at line 167 of file CNF.h.

Here is the call graph for this function:

Here is the caller graph for this function:

to_double() [1/7]

double carl::to_double ( const cln::cl_I &  n )

inline

Converts the given integer to a double.

Parameters

n	An integer.

Returns

Double.

Definition at line 121 of file operations.h.

to_double() [2/7]

double carl::to_double ( const cln::cl_RA &  n )

inline

Converts the given fraction to a double.

Parameters

n	A fraction.

Returns

Double.

Definition at line 113 of file operations.h.

Here is the caller graph for this function:

to_double() [3/7]

template<typename FloatType >

double carl::to_double ( const FLOAT_T< FloatType > &  _float )

inline

Definition at line 1401 of file FLOAT_T.h.

to_double() [4/7]

double carl::to_double ( const mpq_class &  n )

inline

Conversion functions.

The following function convert types to other types.

Definition at line 114 of file operations.h.

to_double() [5/7]

double carl::to_double ( const mpz_class &  n )

inline

Definition at line 117 of file operations.h.

to_double() [6/7]

double carl::to_double ( double  n )

inline

Definition at line 80 of file operations.h.

to_double() [7/7]

double carl::to_double ( sint  n )

inline

Conversion functions.

The following function convert types to other types.

Definition at line 77 of file operations.h.

to_formula()

template<typename Poly >

Formula<Poly> carl::to_formula ( const QuantifierPrefix &  prefix, const Formula< Poly > &  matrix  )

inline

Definition at line 194 of file PNF.h.

to_int() [1/8]

template<typename Integer >

Integer carl::to_int ( const cln::cl_I &  n )

inline

to_int() [2/8]

template<typename Integer >

Integer carl::to_int ( const cln::cl_RA &  n )

inline

to_int() [3/8]

template<typename Integer , typename FloatType >

Integer carl::to_int ( const FLOAT_T< FloatType > &  _float )

inline

Casts the FLOAT_T to an arbitrary integer type which has a constructor for a native int.

Parameters

_float

Returns

Integer type which holds floor(_float).

Definition at line 1395 of file FLOAT_T.h.

Here is the call graph for this function:

to_int() [4/8]

template<typename Integer , typename Number >

Integer carl::to_int ( const Interval< Number > &  _floatInterval )

inline

Casts the Interval to an arbitrary integer type which has a constructor for a native int.

Parameters

_floatInterval

Returns

Integer type which holds floor(_float).

Definition at line 1500 of file Interval.h.

Here is the call graph for this function:

to_int() [5/8]

template<typename Integer >

Integer carl::to_int ( const mpq_class &  n )

inline

to_int() [6/8]

template<typename Integer >

Integer carl::to_int ( const mpz_class &  n )

inline

to_int() [7/8]

template<typename Number >

int carl::to_int ( const Number &  n )

inline

to_int() [8/8]

template<typename Integer >

Integer carl::to_int ( double  n )

inline

to_int< cln::cl_I >()

template<>

cln::cl_I carl::to_int< cln::cl_I > ( const cln::cl_RA &  n )

inline

Convert a fraction to an integer.

This method assert, that the given fraction is an integer, i.e. that the denominator is one.

Parameters

n	A fraction.

Returns

An integer.

Definition at line 174 of file operations.h.

Here is the call graph for this function:

to_int< mpz_class >()

template<>

mpz_class carl::to_int< mpz_class > ( const mpq_class &  n )

inline

Convert a fraction to an integer.

This method assert, that the given fraction is an integer, i.e. that the denominator is one.

Parameters

n	A fraction.

Returns

An integer.

Definition at line 147 of file operations.h.

Here is the call graph for this function:

Here is the caller graph for this function:

to_int< sint >() [1/5]

template<>

sint carl::to_int< sint > ( const cln::cl_I &  n )

inline

Definition at line 131 of file operations.h.

Here is the caller graph for this function:

to_int< sint >() [2/5]

template<>

sint carl::to_int< sint > ( const cln::cl_RA &  n )

inline

Definition at line 179 of file operations.h.

Here is the call graph for this function:

to_int< sint >() [3/5]

template<>

sint carl::to_int< sint > ( const mpq_class &  n )

inline

Convert a fraction to an unsigned.

Parameters

n	A fraction.

Returns

n as unsigned.

Definition at line 191 of file operations.h.

Here is the call graph for this function:

to_int< sint >() [4/5]

template<>

sint carl::to_int< sint > ( const mpz_class &  n )

inline

Definition at line 125 of file operations.h.

to_int< sint >() [5/5]

template<>

sint carl::to_int< sint > ( double  n )

inline

Definition at line 88 of file operations.h.

to_int< uint >() [1/5]

template<>

uint carl::to_int< uint > ( const cln::cl_I &  n )

inline

Definition at line 137 of file operations.h.

Here is the caller graph for this function:

to_int< uint >() [2/5]

template<>

uint carl::to_int< uint > ( const cln::cl_RA &  n )

inline

Definition at line 183 of file operations.h.

Here is the call graph for this function:

to_int< uint >() [3/5]

template<>

uint carl::to_int< uint > ( const mpq_class &  n )

inline

Definition at line 195 of file operations.h.

Here is the call graph for this function:

to_int< uint >() [4/5]

template<>

uint carl::to_int< uint > ( const mpz_class &  n )

inline

Definition at line 131 of file operations.h.

to_int< uint >() [5/5]

template<>

uint carl::to_int< uint > ( double  n )

inline

Definition at line 93 of file operations.h.

to_lf()

cln::cl_LF carl::to_lf ( const cln::cl_RA &  n )

inline

Convert a cln fraction to a cln long float.

Parameters

n	A fraction.

Returns

n as cln::cl_LF.

Definition at line 192 of file operations.h.

to_nnf()

template<typename Poly >

Formula<Poly> carl::to_nnf

(

const Formula< Poly > &

formula

)

Definition at line 9 of file NNF.h.

Here is the call graph for this function:

to_pnf() [1/2]

template<typename Poly >

std::pair<QuantifierPrefix, Formula<Poly> > carl::to_pnf

(

const Formula< Poly > &

f

)

Transforms this formula to its equivalent in prenex normal form.

Parameters

negated

Used for internal recursion.

Returns

A pair of the prefix and the matrix.

Definition at line 186 of file PNF.h.

Here is the call graph for this function:

to_pnf() [2/2]

template<typename Poly >

Formula<Poly> carl::to_pnf	(	const Formula< Poly > &	f,
		QuantifierPrefix &	prefix,
		boost::container::flat_set< Variable > &	used_vars,
		bool	negated = false
	)

Definition at line 31 of file PNF.h.

Here is the call graph for this function:

Here is the caller graph for this function:

to_univariate_polynomial() [1/2]

template<typename C , typename O , typename P >

UnivariatePolynomial<C> carl::to_univariate_polynomial

(

const MultivariatePolynomial< C, O, P > &

p

)

Convert a univariate polynomial that is currently (mis)represented by a 'MultivariatePolynomial' into a more appropiate 'UnivariatePolynomial' representation.

Note that the current polynomial must mention one and only one variable, i.e., be indeed univariate.

Definition at line 17 of file to_univariate_polynomial.h.

Here is the call graph for this function:

Here is the caller graph for this function:

to_univariate_polynomial() [2/2]

template<typename C , typename O , typename P >

UnivariatePolynomial<MultivariatePolynomial<C,O,P> > carl::to_univariate_polynomial	(	const MultivariatePolynomial< C, O, P > &	p,
		Variable	v
	)

Convert a multivariate polynomial that is currently represented by a MultivariatePolynomial into a UnivariatePolynomial representation.

The main variable of the resulting polynomial is given as second argument.

Definition at line 35 of file to_univariate_polynomial.h.

Here is the call graph for this function:

toId()

std::size_t carl::toId ( const BVCompareRelation  _relation )

inline

Definition at line 52 of file BVCompareRelation.h.

toString() [1/8]

std::string carl::toString ( BVCompareRelation  _r )

inline

Definition at line 29 of file BVCompareRelation.h.

toString() [2/8]

std::string carl::toString	(	const cln::cl_I &	_number,
		bool	_infix = true
	)

toString() [3/8]

std::string carl::toString	(	const cln::cl_RA &	_number,
		bool	_infix = true
	)

toString() [4/8]

template<typename IntegerType >

std::string carl::toString	(	const GFNumber< IntegerType > &	_number,
		bool
	)

Creates the string representation to the given galois field number.

Parameters

_number

The galois field number to get its string representation for.

Returns

The string representation to the given galois field number.

Definition at line 210 of file GFNumber.h.

toString() [5/8]

std::string carl::toString	(	const mpq_class &	_number,
		bool	_infix
	)

Definition at line 175 of file operations.cpp.

Here is the call graph for this function:

toString() [6/8]

std::string carl::toString	(	const mpz_class &	_number,
		bool	_infix
	)

Definition at line 192 of file operations.cpp.

Here is the call graph for this function:

toString() [7/8]

template<typename T >

std::enable_if<std::is_arithmetic<typename remove_all<T>::type>::value, std::string>::type carl::toString ( const T &  n, bool    )

inline

Definition at line 103 of file operations.h.

toString() [8/8]

std::string carl::toString ( Relation  r )

inline

Definition at line 73 of file Relation.h.

Here is the caller graph for this function:

total_degree() [1/4]

auto carl::total_degree ( const Monomial &  m )

inline

Gives the total degree, i.e.

the sum of all exponents.

Returns

Total degree.

Definition at line 24 of file Degree.h.

Here is the call graph for this function:

Here is the caller graph for this function:

total_degree() [2/4]

template<typename Coeff , typename Ordering , typename Policies >

std::size_t carl::total_degree

(

const MultivariatePolynomial< Coeff, Ordering, Policies > &

p

)

Calculates the max.

degree over all monomials occurring in the polynomial. As the degree of the zero polynomial is , we assert that this polynomial is not zero. This must be checked by the caller before calling this method.

See also

[3], page 48

Returns

Total degree.

Definition at line 114 of file Degree.h.

Here is the call graph for this function:

total_degree() [3/4]

template<typename Coeff >

std::size_t carl::total_degree

(

const Term< Coeff > &

t

)

Gives the total degree, i.e.

the sum of all exponents.

Returns

Total degree.

Definition at line 57 of file Degree.h.

Here is the call graph for this function:

total_degree() [4/4]

template<typename Coeff >

std::size_t carl::total_degree

(

const UnivariatePolynomial< Coeff > &

p

)

Returns the total degree of the polynomial, that is the maximum degree of any monomial.

As the degree of the zero polynomial is , we assert that this polynomial is not zero. This must be checked by the caller before calling this method.

See also

[3], page 38

Returns

Total degree.

Definition at line 164 of file Degree.h.

Here is the call graph for this function:

try_divide() [1/4]

template<typename Coeff , typename Ordering , typename Policies >

bool carl::try_divide	(	const MultivariatePolynomial< Coeff, Ordering, Policies > &	dividend,
		const MultivariatePolynomial< Coeff, Ordering, Policies > &	divisor,
		MultivariatePolynomial< Coeff, Ordering, Policies > &	quotient
	)

Divides the polynomial by another polynomial.

If the divisor divides this polynomial, quotient contains the result of the division and true is returned. Otherwise, false is returned and the content of quotient remains unchanged. Applies if the coefficients are from a field. Note that the quotient must not be *this.

Parameters

divisor
quotient

Returns

Definition at line 74 of file Division.h.

Here is the call graph for this function:

try_divide() [2/4]

template<typename Coeff >

bool carl::try_divide	(	const Term< Coeff > &	t,
		const Coeff &	c,
		Term< Coeff > &	res
	)

Definition at line 28 of file Division.h.

Here is the call graph for this function:

Here is the caller graph for this function:

try_divide() [3/4]

template<typename Coeff >

bool carl::try_divide	(	const Term< Coeff > &	t,
		Variable	v,
		Term< Coeff > &	res
	)

Definition at line 36 of file Division.h.

Here is the call graph for this function:

try_divide() [4/4]

template<typename Coeff >

bool carl::try_divide	(	const UnivariatePolynomial< Coeff > &	dividend,
		const Coeff &	divisor,
		UnivariatePolynomial< Coeff > &	quotient
	)

Definition at line 144 of file Division.h.

Here is the call graph for this function:

try_parse()

template<typename T >

bool carl::try_parse ( const std::string &  n, T &  res  )

inline

try_parse< cln::cl_I >()

template<>

bool carl::try_parse< cln::cl_I >	(	const std::string &	n,
		cln::cl_I &	res
	)

try_parse< cln::cl_RA >()

template<>

bool carl::try_parse< cln::cl_RA >	(	const std::string &	n,
		cln::cl_RA &	res
	)

try_parse< mpq_class >()

template<>

bool carl::try_parse< mpq_class >	(	const std::string &	n,
		mpq_class &	res
	)

Definition at line 171 of file operations.cpp.

Here is the call graph for this function:

try_parse< mpz_class >()

template<>

bool carl::try_parse< mpz_class >	(	const std::string &	n,
		mpz_class &	res
	)

Definition at line 158 of file operations.cpp.

Here is the call graph for this function:

tuple_accumulate()

template<typename Tuple , typename T , typename F >

T carl::tuple_accumulate	(	Tuple &&	t,
		T &&	init,
		F &&	f
	)

Implements a functional fold (similar to std::accumulate) for std::tuple.

Combines all tuple elements using a combinator function f and an initial value init.

Definition at line 139 of file tuple_util.h.

Here is the call graph for this function:

Here is the caller graph for this function:

tuple_apply()

template<typename F , typename Tuple >

auto carl::tuple_apply	(	F &&	f,
		Tuple &&	t
	)

Invokes a callable object f on a tuple of arguments.

This is basically std::apply (available with C++17).

Definition at line 90 of file tuple_util.h.

Here is the call graph for this function:

tuple_cat()

template<typename Tuple1 , typename Tuple2 >

auto carl::tuple_cat	(	Tuple1 &&	t1,
		Tuple2 &&	t2
	)

Definition at line 23 of file tuple_util.h.

Here is the call graph for this function:

Here is the caller graph for this function:

tuple_foreach()

template<typename F , typename Tuple >

auto carl::tuple_foreach	(	F &&	f,
		Tuple &&	t
	)

Invokes a callable object f on every element of a tuple and returns a tuple containing the results.

This basically corresponds to the functional map(func, list).`

Definition at line 110 of file tuple_util.h.

Here is the call graph for this function:

tuple_tail()

template<typename Tuple >

auto carl::tuple_tail

(

Tuple &&

t

)

Returns a new tuple containing everything but the first element.

Definition at line 46 of file tuple_util.h.

Here is the call graph for this function:

Here is the caller graph for this function:

turn_around()

Relation carl::turn_around ( Relation  r )

inline

Turns around the given relation symbol, in the sense that LESS (LEQ) and GREATER (GEQ) are swapped.

Definition at line 58 of file Relation.h.

Here is the caller graph for this function:

typeId()

auto carl::typeId ( BVTermType  type )

inline

Definition at line 25 of file BVTermType.h.

Here is the caller graph for this function:

typeIsBinary()

bool carl::typeIsBinary ( BVTermType  type )

inline

Definition at line 74 of file BVTermType.h.

Here is the caller graph for this function:

typeIsUnary()

bool carl::typeIsUnary ( BVTermType  type )

inline

Definition at line 66 of file BVTermType.h.

Here is the caller graph for this function:

typeString()

template<typename T >

std::string carl::typeString

(

)

Definition at line 38 of file debug.h.

Here is the call graph for this function:

underlying_enum_value()

template<typename Enum >

constexpr auto carl::underlying_enum_value ( Enum  e )

constexpr

Casts an enum value to a value of the underlying number type.

Definition at line 21 of file enum_util.h.

Here is the caller graph for this function:

uninterpreted_functions()

template<typename Pol >

void carl::uninterpreted_functions	(	const Formula< Pol > &	f,
		std::set< UninterpretedFunction > &	ufs
	)

Definition at line 42 of file Variables.h.

Here is the call graph for this function:

Here is the caller graph for this function:

uninterpreted_variables() [1/2]

template<typename Pol >

void carl::uninterpreted_variables	(	const Formula< Pol > &	f,
		std::set< UVariable > &	uvs
	)

Definition at line 53 of file Variables.h.

Here is the call graph for this function:

uninterpreted_variables() [2/2]

template<typename T >

carlVariables carl::uninterpreted_variables ( const T &  t )

inline

Definition at line 261 of file Variables.h.

Here is the call graph for this function:

Here is the caller graph for this function:

univariateTarskiQuery() [1/2]

template<typename Number >

int carl::univariateTarskiQuery	(	const UnivariatePolynomial< Number > &	p,
		const UnivariatePolynomial< Number > &	q
	)

Definition at line 48 of file UnivariateTarskiQuery.h.

Here is the call graph for this function:

univariateTarskiQuery() [2/2]

template<typename Number >

int carl::univariateTarskiQuery	(	const UnivariatePolynomial< Number > &	p,
		const UnivariatePolynomial< Number > &	q,
		const UnivariatePolynomial< Number > &	der_q
	)

Definition at line 38 of file UnivariateTarskiQuery.h.

Here is the call graph for this function:

Here is the caller graph for this function:

var_info()

template<typename Coeff , typename Ordering , typename Policies >

VarInfo<MultivariatePolynomial<Coeff,Ordering,Policies> > carl::var_info ( const MultivariatePolynomial< Coeff, Ordering, Policies > &  poly, const Variable  var, bool  collect_coeff = false  )

inline

Definition at line 54 of file VarInfo.h.

Here is the call graph for this function:

Here is the caller graph for this function:

variables() [1/13]

template<typename Pol >

void carl::variables	(	const BasicConstraint< Pol > &	c,
		carlVariables &	vars
	)

Definition at line 139 of file BasicConstraint.h.

Here is the call graph for this function:

Here is the caller graph for this function:

variables() [2/13]

template<typename Pol >

void carl::variables	(	const Constraint< Pol > &	c,
		carlVariables &	vars
	)

Definition at line 329 of file Constraint.h.

Here is the call graph for this function:

variables() [3/13]

template<typename Coeff , typename Ordering , typename Policies >

void carl::variables ( const ContextPolynomial< Coeff, Ordering, Policies > &  p, carlVariables &  vars  )

inline

Definition at line 135 of file ContextPolynomial.h.

Here is the call graph for this function:

variables() [4/13]

template<typename Pol >

void carl::variables	(	const Formula< Pol > &	f,
		carlVariables &	vars
	)

Definition at line 9 of file Variables.h.

Here is the call graph for this function:

variables() [5/13]

void carl::variables ( const Monomial &  m, carlVariables &  vars  )

inline

Add the variables of the given monomial to the variables.

Definition at line 648 of file Monomial.h.

Here is the call graph for this function:

variables() [6/13]

template<typename Coeff , typename Ordering , typename Policies >

void carl::variables	(	const MultivariatePolynomial< Coeff, Ordering, Policies > &	p,
		carlVariables &	vars
	)

Add the variables of the given polynomial to the variables.

Definition at line 637 of file MultivariatePolynomial.h.

Here is the call graph for this function:

variables() [7/13]

template<typename Poly >

void carl::variables	(	const MultivariateRoot< Poly > &	mr,
		carlVariables &	vars
	)

Add the variables mentioned in underlying polynomial, excluding the root-variable "_z".

For example, with an underlying poly p(x,y,_z) we return {x,y}.

Definition at line 114 of file MultivariateRoot.h.

Here is the call graph for this function:

variables() [8/13]

template<typename Poly >

void carl::variables	(	const SqrtEx< Poly > &	ex,
		carlVariables &	vars
	)

Definition at line 251 of file SqrtEx.h.

Here is the call graph for this function:

variables() [9/13]

template<typename T >

carlVariables carl::variables ( const T &  t )

inline

Return the variables as collected by the methods above.

Definition at line 219 of file Variables.h.

Here is the call graph for this function:

variables() [10/13]

template<typename Coeff >

void carl::variables	(	const Term< Coeff > &	t,
		carlVariables &	vars
	)

Add the variables of the given term to the variables.

Definition at line 307 of file Term.h.

Here is the call graph for this function:

variables() [11/13]

template<typename Coeff >

void carl::variables	(	const UnivariatePolynomial< Coeff > &	p,
		carlVariables &	vars
	)

Add the variables of the given polynomial to the variables.

Definition at line 823 of file UnivariatePolynomial.h.

Here is the call graph for this function:

variables() [12/13]

template<typename Pol >

void carl::variables ( const VariableAssignment< Pol > &  f, carlVariables &  vars  )

inline

Definition at line 47 of file VariableAssignment.h.

variables() [13/13]

template<typename Pol >

void carl::variables ( const VariableComparison< Pol > &  f, carlVariables &  vars  )

inline

Definition at line 185 of file VariableComparison.h.

Here is the call graph for this function:

variant_extend()

template<typename Target , typename... Args>

Target carl::variant_extend

(

const boost::variant< Args... > &

variant

)

Definition at line 36 of file variant_util.h.

variant_hash()

template<typename... T>

std::size_t carl::variant_hash ( const boost::variant< T... > &  value )

inline

Definition at line 50 of file variant_util.h.

variant_is_type()

template<typename T , typename Variant >

bool carl::variant_is_type ( const Variant &  variant )

noexcept

Checks whether a variant contains a value of a fiven type.

Definition at line 22 of file variant_util.h.

vars_info()

template<typename Coeff , typename Ordering , typename Policies >

VarsInfo<MultivariatePolynomial<Coeff,Ordering,Policies> > carl::vars_info ( const MultivariatePolynomial< Coeff, Ordering, Policies > &  poly, bool  collect_coeff = false  )

inline

Definition at line 63 of file VarInfo.h.

Here is the call graph for this function:

Here is the caller graph for this function:

visit()

template<typename Pol , typename Visitor >

void carl::visit	(	const Formula< Pol > &	formula,
		Visitor	func
	)

Recursively calls func on every subformula.

Parameters

formula	Formula to visit.
func	Function to call.

Definition at line 12 of file Visit.h.

Here is the call graph for this function:

Here is the caller graph for this function:

visit_result()

template<typename Pol , typename Visitor >

Formula<Pol> carl::visit_result	(	const Formula< Pol > &	formula,
		Visitor	func
	)

Recursively calls func on every subformula and return a new formula.

On every call of func, the passed formula is replaced by the result.

Parameters

formula	Formula to visit.
func	Function to call.

Returns

New formula.

Definition at line 49 of file Visit.h.

Here is the call graph for this function:

Here is the caller graph for this function:

Variable Documentation

A_AND_B__IFF_C

const signed carl::A_AND_B__IFF_C = -3

Definition at line 11 of file Comparison.h.

A_IFF_B

const signed carl::A_IFF_B = 2

Definition at line 7 of file Comparison.h.

A_IMPLIES_B

const signed carl::A_IMPLIES_B = 1

Definition at line 8 of file Comparison.h.

A_XOR_B

const signed carl::A_XOR_B = -4

Definition at line 12 of file Comparison.h.

B_IMPLIES_A

const signed carl::B_IMPLIES_A = -1

Definition at line 9 of file Comparison.h.

CONDITION_SIZE

constexpr std::size_t carl::CONDITION_SIZE = 64

staticconstexpr

Definition at line 17 of file Condition.h.

dependent_false_v

template<class >

constexpr bool carl::dependent_false_v = false

inlineconstexpr

Definition at line 111 of file SFINAE.h.

dummy

const dtl::enabled carl::dummy = {}

Definition at line 53 of file SFINAE.h.

initvariable

int carl::initvariable = initialize()

static

Call to initialize.

Definition at line 57 of file initialize.h.

last_assertion_code

int carl::last_assertion_code = 23

Stores an integer representation of the last assertion that was registered via REGISTER_ASSERT.

Definition at line 36 of file debug.cpp.

last_assertion_string

std::string carl::last_assertion_string

Stores a textual representation of the last assertion that was registered via REGISTER_ASSERT.

Definition at line 35 of file debug.cpp.

mMap

std::map<Variable, Interval<double> > carl::mMap = {{ Variable::NO_VARIABLE , Interval<double>(0)}}

static

Definition at line 20 of file MultivariateHorner.h.

NOT__A_AND_B

const signed carl::NOT__A_AND_B = -2

Definition at line 10 of file Comparison.h.

ONE_DIVIDED_BY_10_TO_THE_POWER_OF_23

const cln::cl_RA carl::ONE_DIVIDED_BY_10_TO_THE_POWER_OF_23 = cln::cl_RA(1)/cln::expt(cln::cl_RA(10), 23)

static

Definition at line 196 of file operations.h.

ONE_DIVIDED_BY_10_TO_THE_POWER_OF_52

const cln::cl_RA carl::ONE_DIVIDED_BY_10_TO_THE_POWER_OF_52 = cln::cl_RA(1)/cln::expt(cln::cl_RA(10), 52)

static

Definition at line 197 of file operations.h.

PROP_CONTAINS_BITVECTOR

constexpr Condition carl::PROP_CONTAINS_BITVECTOR = Condition( 26 )

staticconstexpr

Definition at line 75 of file Condition.h.

PROP_CONTAINS_BOOLEAN

constexpr Condition carl::PROP_CONTAINS_BOOLEAN = Condition( 22 )

staticconstexpr

Definition at line 71 of file Condition.h.

PROP_CONTAINS_EQUATION

constexpr Condition carl::PROP_CONTAINS_EQUATION = Condition( 16 )

staticconstexpr

Definition at line 65 of file Condition.h.

PROP_CONTAINS_INEQUALITY

constexpr Condition carl::PROP_CONTAINS_INEQUALITY = Condition( 17 )

staticconstexpr

Definition at line 66 of file Condition.h.

PROP_CONTAINS_INTEGER_VALUED_VARS

constexpr Condition carl::PROP_CONTAINS_INTEGER_VALUED_VARS = Condition( 23 )

staticconstexpr

Definition at line 72 of file Condition.h.

PROP_CONTAINS_LINEAR_POLYNOMIAL

constexpr Condition carl::PROP_CONTAINS_LINEAR_POLYNOMIAL = Condition( 19 )

staticconstexpr

Definition at line 68 of file Condition.h.

PROP_CONTAINS_MULTIVARIATE_POLYNOMIAL

constexpr Condition carl::PROP_CONTAINS_MULTIVARIATE_POLYNOMIAL = Condition( 21 )

staticconstexpr

Definition at line 70 of file Condition.h.

PROP_CONTAINS_NONLINEAR_POLYNOMIAL

constexpr Condition carl::PROP_CONTAINS_NONLINEAR_POLYNOMIAL = Condition( 20 )

staticconstexpr

Definition at line 69 of file Condition.h.

PROP_CONTAINS_PSEUDOBOOLEAN

constexpr Condition carl::PROP_CONTAINS_PSEUDOBOOLEAN = Condition( 27 )

staticconstexpr

Definition at line 76 of file Condition.h.

PROP_CONTAINS_QUANTIFIER_EXISTS

constexpr Condition carl::PROP_CONTAINS_QUANTIFIER_EXISTS = Condition( 32 )

staticconstexpr

Definition at line 81 of file Condition.h.

PROP_CONTAINS_QUANTIFIER_FORALL

constexpr Condition carl::PROP_CONTAINS_QUANTIFIER_FORALL = Condition( 33 )

staticconstexpr

Definition at line 82 of file Condition.h.

PROP_CONTAINS_REAL_VALUED_VARS

constexpr Condition carl::PROP_CONTAINS_REAL_VALUED_VARS = Condition( 24 )

staticconstexpr

Definition at line 73 of file Condition.h.

PROP_CONTAINS_STRICT_INEQUALITY

constexpr Condition carl::PROP_CONTAINS_STRICT_INEQUALITY = Condition( 18 )

staticconstexpr

Definition at line 67 of file Condition.h.

PROP_CONTAINS_UNINTERPRETED_EQUATIONS

constexpr Condition carl::PROP_CONTAINS_UNINTERPRETED_EQUATIONS = Condition( 25 )

staticconstexpr

Definition at line 74 of file Condition.h.

PROP_CONTAINS_WEAK_INEQUALITY

constexpr Condition carl::PROP_CONTAINS_WEAK_INEQUALITY = Condition( 31 )

staticconstexpr

Definition at line 80 of file Condition.h.

PROP_IS_A_CLAUSE

constexpr Condition carl::PROP_IS_A_CLAUSE = Condition( 3 )

staticconstexpr

Definition at line 55 of file Condition.h.

PROP_IS_A_LITERAL

constexpr Condition carl::PROP_IS_A_LITERAL = Condition( 4 )

staticconstexpr

Definition at line 56 of file Condition.h.

PROP_IS_AN_ATOM

constexpr Condition carl::PROP_IS_AN_ATOM = Condition( 5 )

staticconstexpr

Definition at line 57 of file Condition.h.

PROP_IS_IN_CNF

constexpr Condition carl::PROP_IS_IN_CNF = Condition( 1 )

staticconstexpr

Definition at line 53 of file Condition.h.

PROP_IS_IN_NNF

constexpr Condition carl::PROP_IS_IN_NNF = Condition( 0 )

staticconstexpr

Definition at line 52 of file Condition.h.

PROP_IS_IN_PNF

constexpr Condition carl::PROP_IS_IN_PNF = Condition( 7 )

staticconstexpr

Definition at line 59 of file Condition.h.

PROP_IS_LITERAL_CONJUNCTION

constexpr Condition carl::PROP_IS_LITERAL_CONJUNCTION = Condition( 6 )

staticconstexpr

Definition at line 58 of file Condition.h.

PROP_IS_PURE_CONJUNCTION

constexpr Condition carl::PROP_IS_PURE_CONJUNCTION = Condition( 2 )

staticconstexpr

Definition at line 54 of file Condition.h.

PROP_TRUE

constexpr Condition carl::PROP_TRUE = Condition()

staticconstexpr

Definition at line 49 of file Condition.h.

PROP_VARIABLE_DEGREE_GREATER_THAN_FOUR

constexpr Condition carl::PROP_VARIABLE_DEGREE_GREATER_THAN_FOUR = Condition( 30 )

staticconstexpr

Definition at line 79 of file Condition.h.

PROP_VARIABLE_DEGREE_GREATER_THAN_THREE

constexpr Condition carl::PROP_VARIABLE_DEGREE_GREATER_THAN_THREE = Condition( 29 )

staticconstexpr

Definition at line 78 of file Condition.h.

PROP_VARIABLE_DEGREE_GREATER_THAN_TWO

constexpr Condition carl::PROP_VARIABLE_DEGREE_GREATER_THAN_TWO = Condition( 28 )

staticconstexpr

Definition at line 77 of file Condition.h.

signal_installed

bool carl::signal_installed = install_signal_handler()

static

Static variable that ensures that install_signal_handler is called.

Definition at line 66 of file debug.cpp.

sizeOfUnsigned

constexpr unsigned carl::sizeOfUnsigned = sizeof(unsigned)

constexpr

Definition at line 17 of file BitVector.h.

STRONG_CONDITIONS

const Condition carl::STRONG_CONDITIONS

static

Initial value:

= PROP_IS_IN_NNF | PROP_IS_IN_CNF | PROP_IS_PURE_CONJUNCTION |
                                                                  PROP_IS_A_CLAUSE | PROP_IS_A_LITERAL | PROP_IS_AN_ATOM | PROP_IS_LITERAL_CONJUNCTION |
                                                                  PROP_IS_IN_PNF

Definition at line 60 of file Condition.h.

WEAK_CONDITIONS

const Condition carl::WEAK_CONDITIONS

static

Initial value:

= PROP_CONTAINS_EQUATION | PROP_CONTAINS_INEQUALITY | PROP_CONTAINS_STRICT_INEQUALITY
                                             | PROP_CONTAINS_LINEAR_POLYNOMIAL | PROP_CONTAINS_LINEAR_POLYNOMIAL | PROP_CONTAINS_NONLINEAR_POLYNOMIAL
                                             | PROP_CONTAINS_MULTIVARIATE_POLYNOMIAL | PROP_CONTAINS_INEQUALITY | PROP_CONTAINS_BOOLEAN
                                             | PROP_CONTAINS_REAL_VALUED_VARS | PROP_CONTAINS_INTEGER_VALUED_VARS
                                             | PROP_CONTAINS_UNINTERPRETED_EQUATIONS | PROP_CONTAINS_BITVECTOR | PROP_CONTAINS_PSEUDOBOOLEAN
                                             | PROP_VARIABLE_DEGREE_GREATER_THAN_TWO | PROP_VARIABLE_DEGREE_GREATER_THAN_THREE | PROP_VARIABLE_DEGREE_GREATER_THAN_FOUR | PROP_CONTAINS_QUANTIFIER_EXISTS | PROP_CONTAINS_QUANTIFIER_FORALL

Definition at line 85 of file Condition.h.