is_integer_type
All integral types that can (in theory) represent all integers are marked with is_integer_type.
More...
Collaboration diagram for is_integer_type:
Modules | |
| is_subset_of_integers_type | |
All integral types are marked with is_subset_of_integers_type. | |
Data Structures | |
| struct | carl::is_integer_type< cln::cl_I > |
| States that cln::cl_I has the trait is_integer_type . More... | |
| struct | carl::is_integer_type< mpz_class > |
| States that mpz_class has the trait is_integer_type . More... | |
| struct | carl::is_integer_type< T > |
| States if a type is an integer type. More... | |
Detailed Description
All integral types that can (in theory) represent all integers are marked with is_integer_type.
To be an integer type, the type must satisfy the following conditions:
- It represents exactly all integer numbers.
- It defines the basic operators
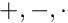 by implementing
by implementing operator+(),operator-()andoperator*()which are closed. - It's operations are associative and commutative. Multiplication and addition are distributive.
- There are identity elements for addition and multiplication.
- For every element of the type, there is an inverse element for addition.
- Additionally, it defines the following operations:
div(): Performs an integer division, asserting that the remainder is zero.quotient(): Calculates the quotient of an integer division.remainder(): Calculates the remainder of an integer division.mod(): Calculated the modulus of an integer.operator/()shall be an alias forquotient().
Data Structure Documentation
◆ carl::is_integer_type< cln::cl_I >
| struct carl::is_integer_type< cln::cl_I > |
States that cln::cl_I has the trait is_integer_type .
<>
Definition at line 20 of file typetraits.h.
Inheritance diagram for carl::is_integer_type< cln::cl_I >:
Collaboration diagram for carl::is_integer_type< cln::cl_I >:
◆ carl::is_integer_type< mpz_class >
| struct carl::is_integer_type< mpz_class > |
States that mpz_class has the trait is_integer_type .
<>
Definition at line 21 of file typetraits.h.
Inheritance diagram for carl::is_integer_type< mpz_class >:
Collaboration diagram for carl::is_integer_type< mpz_class >:
◆ carl::is_integer_type
| struct carl::is_integer_type |
template<typename T>
struct carl::is_integer_type< T >
States if a type is an integer type.
Default is false.
Definition at line 203 of file typetraits.h.
Inheritance diagram for carl::is_integer_type< T >:
Collaboration diagram for carl::is_integer_type< T >: