#include <Ran.h>

Inheritance diagram for carl::IntRepRealAlgebraicNumber< Number >:

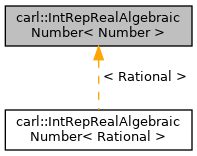
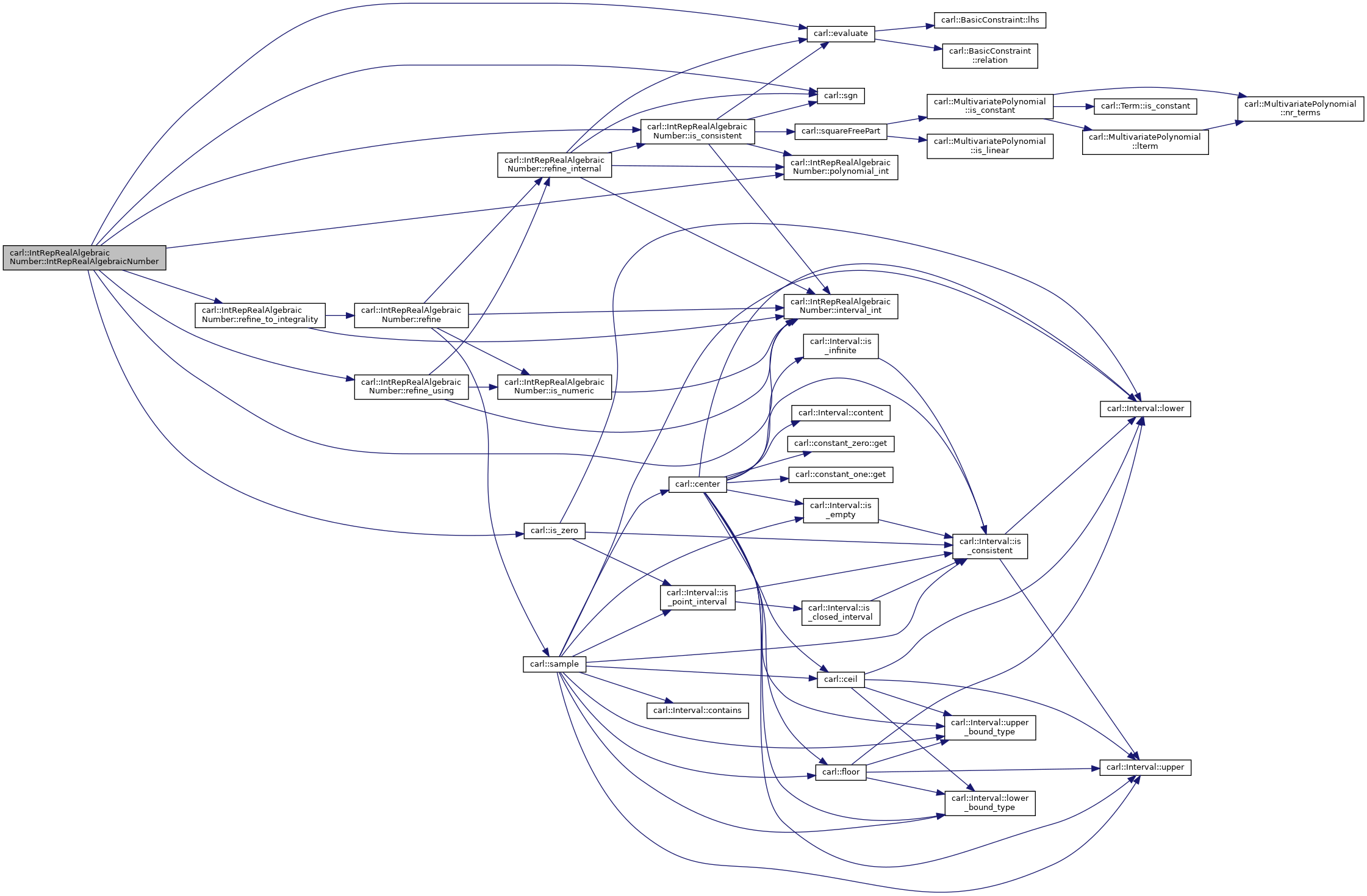
Collaboration diagram for carl::IntRepRealAlgebraicNumber< Number >:

[legend]

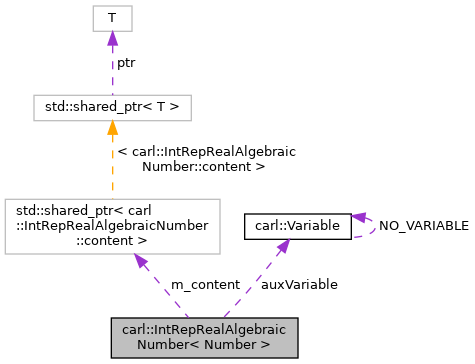
Data Structures
struct	content

Public Member Functions
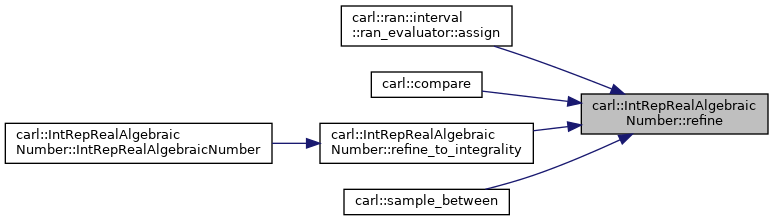
void	refine () const

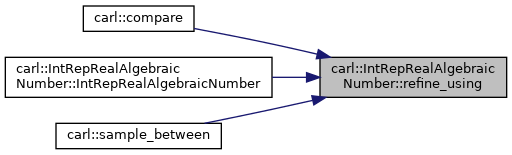
std::optional< Sign >	refine_using (const Number &pivot) const

	IntRepRealAlgebraicNumber ()

	IntRepRealAlgebraicNumber (const Number &n)

	IntRepRealAlgebraicNumber (const UnivariatePolynomial< Number > &p, const Interval< Number > &i)

	IntRepRealAlgebraicNumber (const IntRepRealAlgebraicNumber &ran)=default

	IntRepRealAlgebraicNumber (IntRepRealAlgebraicNumber &&ran)=default

IntRepRealAlgebraicNumber &	operator= (const IntRepRealAlgebraicNumber &n)=default

IntRepRealAlgebraicNumber &	operator= (IntRepRealAlgebraicNumber &&n)=default

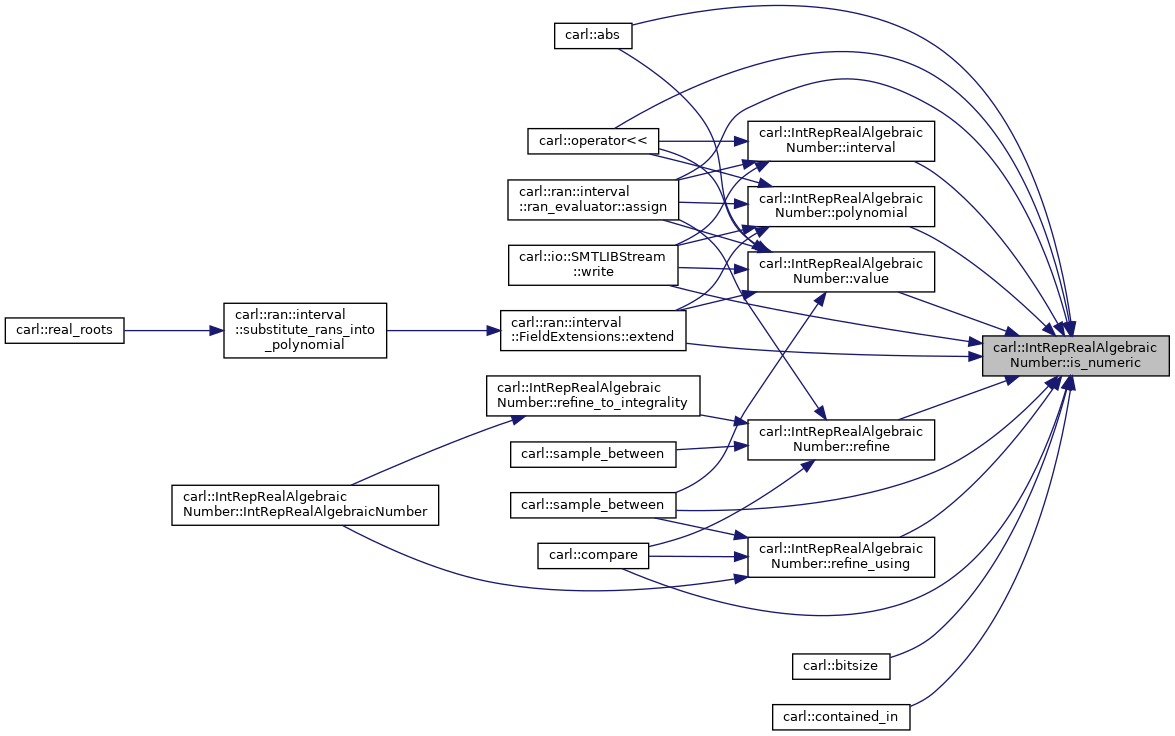
bool	is_numeric () const

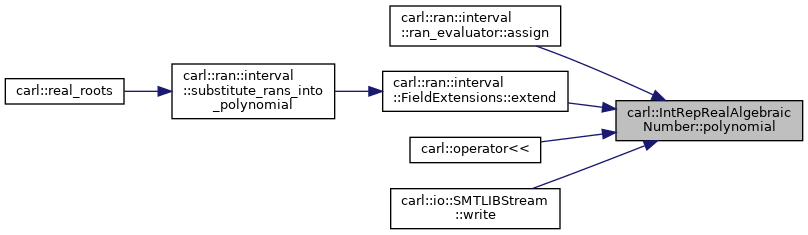
const auto &	polynomial () const

const auto &	interval () const

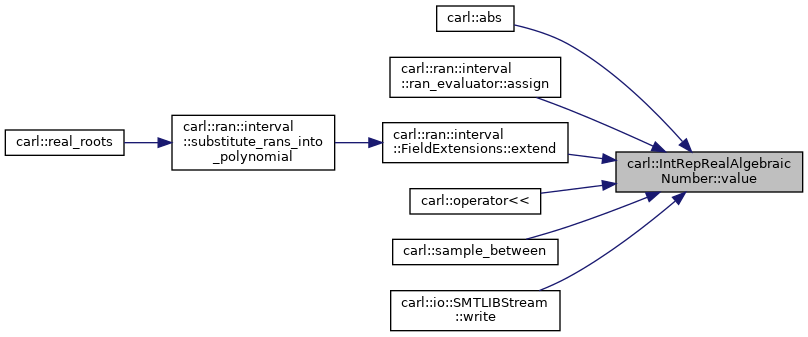
const auto &	value () const

auto &	polynomial_int () const

auto &	interval_int () const

Static Public Member Functions
static IntRepRealAlgebraicNumber< Number >	create_safe (const UnivariatePolynomial< Number > &p, const Interval< Number > &i)

Private Member Functions
bool	is_consistent () const

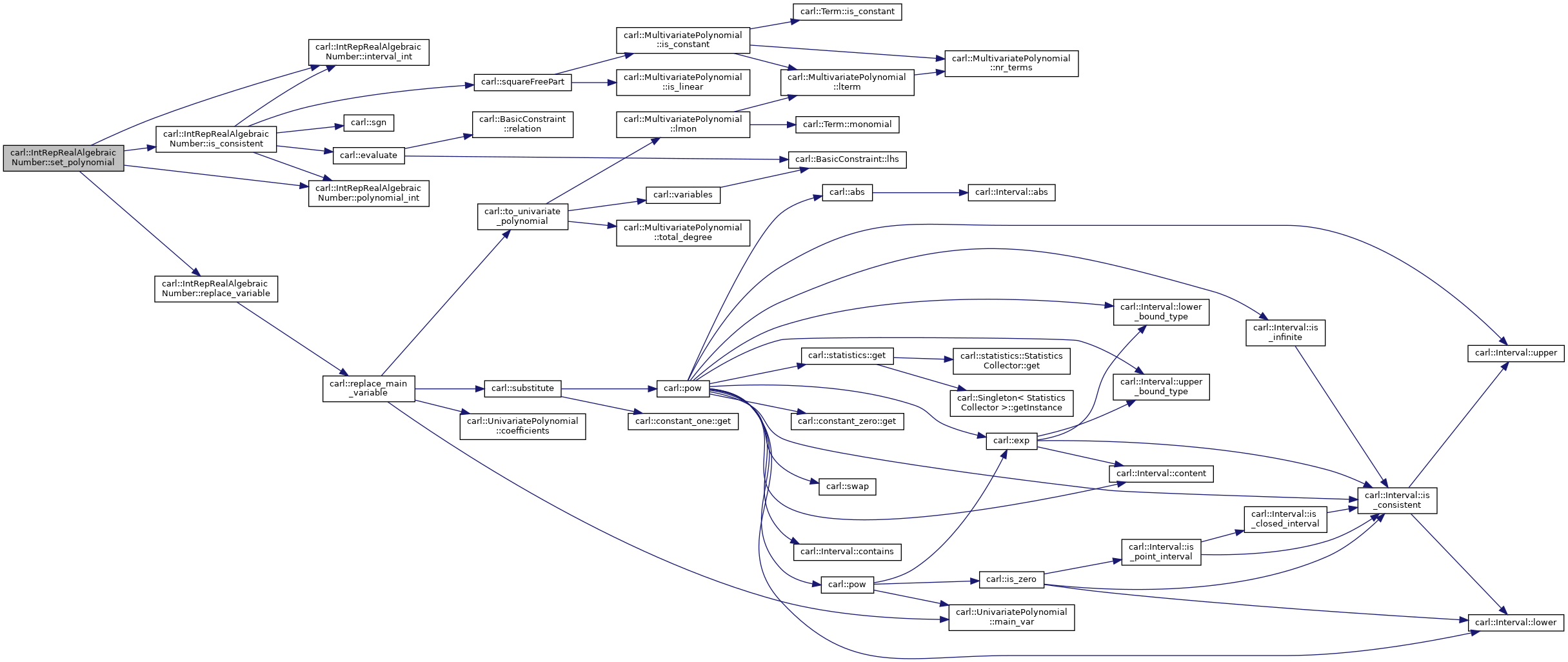
void	set_polynomial (const UnivariatePolynomial< Number > &p, Sign lower_sign) const

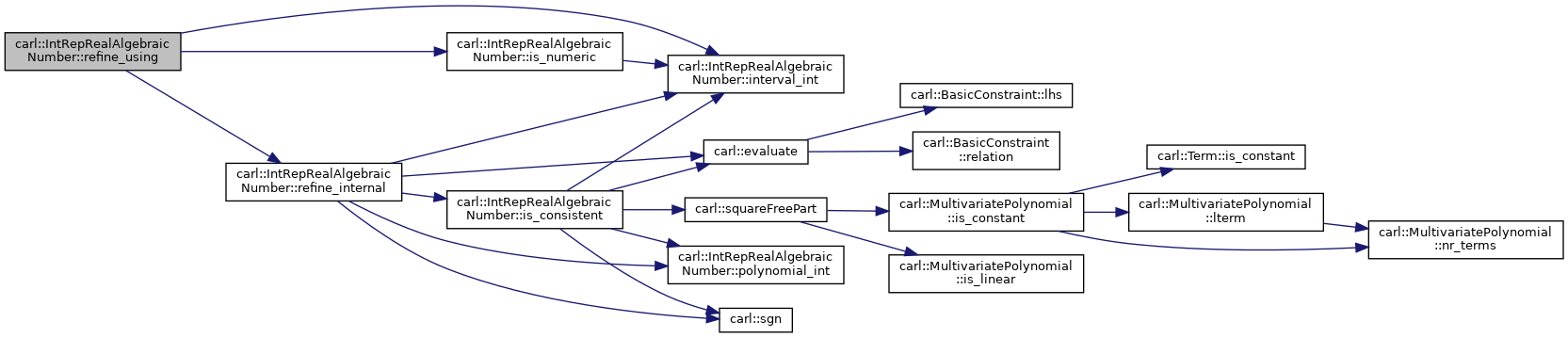
Sign	refine_internal (const Number &pivot) const
	Returns the sign of "interval_int() - pivot": Returns ZERO if pivot is equal to RAN. More...

void	refine_to_integrality () const
	Refines until the number is either numeric or the interval does not contain any integer. More...

Static Private Member Functions
static UnivariatePolynomial< Number >	replace_variable (const UnivariatePolynomial< Number > &p)

Private Attributes
std::shared_ptr< content >	m_content

Static Private Attributes
static const Variable	auxVariable = fresh_real_variable("__r")

Friends
template<typename Num >
bool	compare (const IntRepRealAlgebraicNumber< Num > &, const IntRepRealAlgebraicNumber< Num > &, const Relation)

template<typename Num >
bool	compare (const IntRepRealAlgebraicNumber< Num > &, const Num &, const Relation)

template<typename Num , typename Poly >
boost::tribool	evaluate (const BasicConstraint< Poly > &, const Assignment< IntRepRealAlgebraicNumber< Num >> &, bool, bool)

template<typename Num >
std::optional< IntRepRealAlgebraicNumber< Num > >	evaluate (MultivariatePolynomial< Num >, const Assignment< IntRepRealAlgebraicNumber< Num >> &, bool)

template<typename Num >
Num	branching_point (const IntRepRealAlgebraicNumber< Num > &n)

template<typename Num >
Num	sample_above (const IntRepRealAlgebraicNumber< Num > &n)

template<typename Num >
Num	sample_below (const IntRepRealAlgebraicNumber< Num > &n)

template<typename Num >
Num	sample_between (const IntRepRealAlgebraicNumber< Num > &lower, const IntRepRealAlgebraicNumber< Num > &upper)

template<typename Num >
Num	sample_between (const IntRepRealAlgebraicNumber< Num > &lower, const Num &upper)

template<typename Num >
Num	sample_between (const Num &lower, const IntRepRealAlgebraicNumber< Num > &upper)

template<typename Num >
Num	floor (const IntRepRealAlgebraicNumber< Num > &n)

template<typename Num >
Num	ceil (const IntRepRealAlgebraicNumber< Num > &n)

template<typename Num >
Sign	sgn (const IntRepRealAlgebraicNumber< Num > &n, const UnivariatePolynomial< Num > &p)

Detailed Description

template<typename Number>
class carl::IntRepRealAlgebraicNumber< Number >

Definition at line 25 of file Ran.h.

Constructor & Destructor Documentation

◆ IntRepRealAlgebraicNumber() [1/5]

template<typename Number >

carl::IntRepRealAlgebraicNumber< Number >::IntRepRealAlgebraicNumber ( )

inline

Definition at line 177 of file Ran.h.

◆ IntRepRealAlgebraicNumber() [2/5]

template<typename Number >

carl::IntRepRealAlgebraicNumber< Number >::IntRepRealAlgebraicNumber ( const Number & n )

inline

Definition at line 180 of file Ran.h.

◆ IntRepRealAlgebraicNumber() [3/5]

template<typename Number >

carl::IntRepRealAlgebraicNumber< Number >::IntRepRealAlgebraicNumber	(	const UnivariatePolynomial< Number > &	p,
		const Interval< Number > &	i
	)

inline

Definition at line 183 of file Ran.h.

Here is the call graph for this function:

◆ IntRepRealAlgebraicNumber() [4/5]

template<typename Number >

carl::IntRepRealAlgebraicNumber< Number >::IntRepRealAlgebraicNumber ( const IntRepRealAlgebraicNumber< Number > & ran )

default

◆ IntRepRealAlgebraicNumber() [5/5]

template<typename Number >

carl::IntRepRealAlgebraicNumber< Number >::IntRepRealAlgebraicNumber ( IntRepRealAlgebraicNumber< Number > && ran )

default

Member Function Documentation

◆ create_safe()

template<typename Number >

static IntRepRealAlgebraicNumber<Number> carl::IntRepRealAlgebraicNumber< Number >::create_safe	(	const UnivariatePolynomial< Number > &	p,
		const Interval< Number > &	i
	)

inlinestatic

Definition at line 210 of file Ran.h.

Here is the call graph for this function:

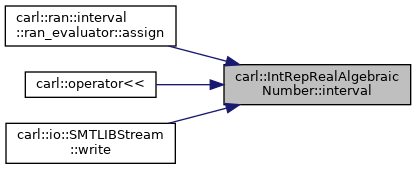
◆ interval()

template<typename Number >

const auto& carl::IntRepRealAlgebraicNumber< Number >::interval ( ) const

inline

Definition at line 222 of file Ran.h.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ interval_int()

template<typename Number >

auto& carl::IntRepRealAlgebraicNumber< Number >::interval_int ( ) const

inline

Definition at line 235 of file Ran.h.

Here is the caller graph for this function:

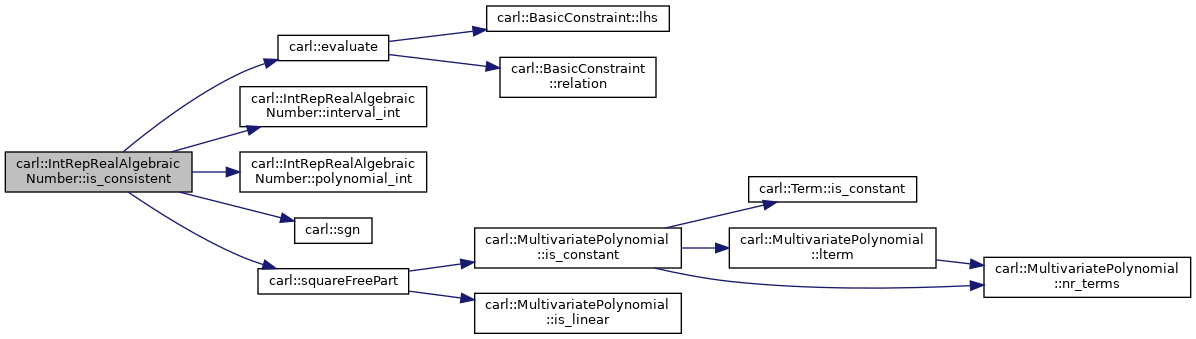
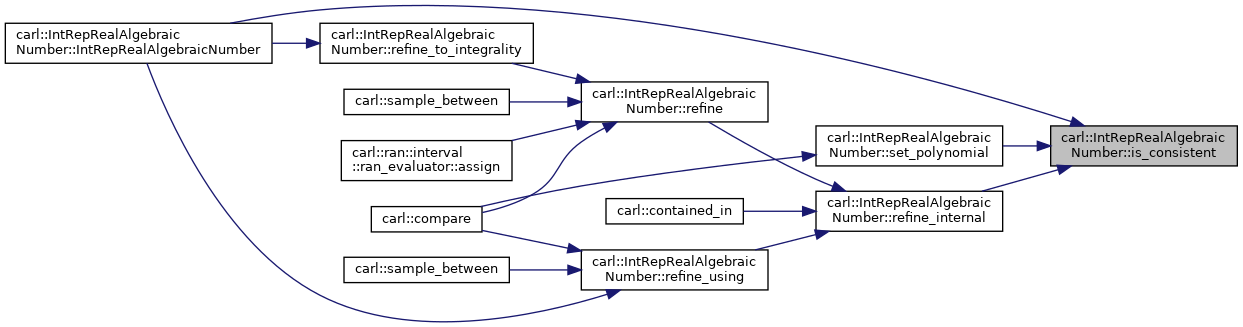
◆ is_consistent()

template<typename Number >

bool carl::IntRepRealAlgebraicNumber< Number >::is_consistent ( ) const

inlineprivate

Definition at line 93 of file Ran.h.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ is_numeric()

template<typename Number >

bool carl::IntRepRealAlgebraicNumber< Number >::is_numeric ( ) const

inline

Definition at line 214 of file Ran.h.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ operator=() [1/2]

template<typename Number >

IntRepRealAlgebraicNumber& carl::IntRepRealAlgebraicNumber< Number >::operator= ( const IntRepRealAlgebraicNumber< Number > & n )

default

◆ operator=() [2/2]

template<typename Number >

IntRepRealAlgebraicNumber& carl::IntRepRealAlgebraicNumber< Number >::operator= ( IntRepRealAlgebraicNumber< Number > && n )

default

◆ polynomial()

template<typename Number >

const auto& carl::IntRepRealAlgebraicNumber< Number >::polynomial ( ) const

inline

Definition at line 218 of file Ran.h.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ polynomial_int()

template<typename Number >

auto& carl::IntRepRealAlgebraicNumber< Number >::polynomial_int ( ) const

inline

Definition at line 232 of file Ran.h.

Here is the caller graph for this function:

◆ refine()

template<typename Number >

void carl::IntRepRealAlgebraicNumber< Number >::refine ( ) const

inline

Definition at line 154 of file Ran.h.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ refine_internal()

template<typename Number >

Sign carl::IntRepRealAlgebraicNumber< Number >::refine_internal ( const Number & pivot ) const

inlineprivate

Returns the sign of "interval_int() - pivot": Returns ZERO if pivot is equal to RAN.

Returns POSITIVE if pivot is less than RAN resp. the new lower bound. Returns NEGATIVE if pivot is greater than RAN resp. the new upper bound.

Definition at line 132 of file Ran.h.

Here is the call graph for this function:

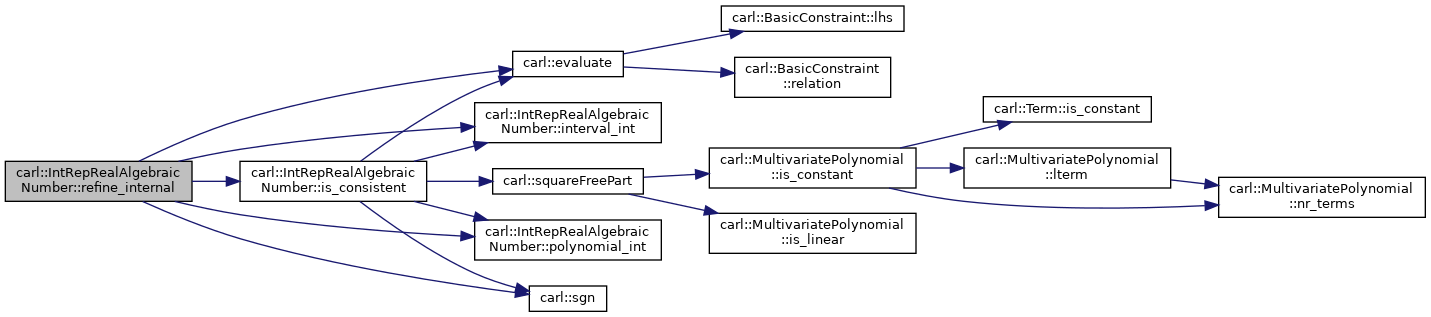
Here is the caller graph for this function:

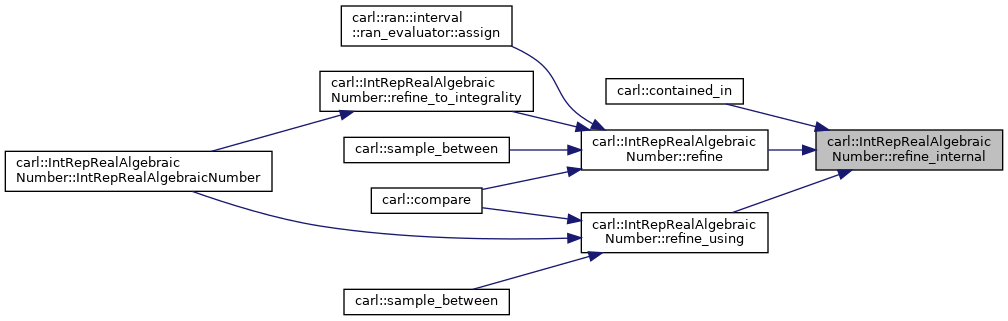
◆ refine_to_integrality()

template<typename Number >

void carl::IntRepRealAlgebraicNumber< Number >::refine_to_integrality ( ) const

inlineprivate

Refines until the number is either numeric or the interval does not contain any integer.

Definition at line 170 of file Ran.h.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ refine_using()

template<typename Number >

std::optional<Sign> carl::IntRepRealAlgebraicNumber< Number >::refine_using ( const Number & pivot ) const

inline

Definition at line 160 of file Ran.h.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ replace_variable()

template<typename Number >

static UnivariatePolynomial<Number> carl::IntRepRealAlgebraicNumber< Number >::replace_variable ( const UnivariatePolynomial< Number > & p )

inlinestaticprivate

Definition at line 89 of file Ran.h.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ set_polynomial()

template<typename Number >

void carl::IntRepRealAlgebraicNumber< Number >::set_polynomial	(	const UnivariatePolynomial< Number > &	p,
		Sign	lower_sign
	)		const

inlineprivate

Definition at line 119 of file Ran.h.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ value()

template<typename Number >

const auto& carl::IntRepRealAlgebraicNumber< Number >::value ( ) const

inline

Definition at line 227 of file Ran.h.

Here is the call graph for this function:

Here is the caller graph for this function:

Friends And Related Function Documentation

◆ branching_point

template<typename Number >

template<typename Num >

Num branching_point ( const IntRepRealAlgebraicNumber< Num > & n )

friend

◆ ceil

template<typename Number >

template<typename Num >

Num ceil ( const IntRepRealAlgebraicNumber< Num > & n )

friend

◆ compare [1/2]

template<typename Number >

template<typename Num >

bool compare	(	const IntRepRealAlgebraicNumber< Num > &	,
		const IntRepRealAlgebraicNumber< Num > &	,
		const	Relation
	)

friend

◆ compare [2/2]

template<typename Number >

template<typename Num >

bool compare	(	const IntRepRealAlgebraicNumber< Num > &	,
		const Num &	,
		const	Relation
	)

friend

◆ evaluate [1/2]

template<typename Number >

template<typename Num , typename Poly >

boost::tribool evaluate	(	const BasicConstraint< Poly > &	,
		const Assignment< IntRepRealAlgebraicNumber< Num >> &	,
		bool	,
		bool
	)

friend

◆ evaluate [2/2]

template<typename Number >

template<typename Num >

std::optional<IntRepRealAlgebraicNumber<Num> > evaluate	(	MultivariatePolynomial< Num >	,
		const Assignment< IntRepRealAlgebraicNumber< Num >> &	,
		bool
	)

friend

◆ floor

template<typename Number >

template<typename Num >

Num floor ( const IntRepRealAlgebraicNumber< Num > & n )

friend

◆ sample_above

template<typename Number >

template<typename Num >

Num sample_above ( const IntRepRealAlgebraicNumber< Num > & n )

friend

◆ sample_below

template<typename Number >

template<typename Num >

Num sample_below ( const IntRepRealAlgebraicNumber< Num > & n )

friend

◆ sample_between [1/3]

template<typename Number >

template<typename Num >

Num sample_between	(	const IntRepRealAlgebraicNumber< Num > &	lower,
		const IntRepRealAlgebraicNumber< Num > &	upper
	)

friend

◆ sample_between [2/3]

template<typename Number >

template<typename Num >

Num sample_between	(	const IntRepRealAlgebraicNumber< Num > &	lower,
		const Num &	upper
	)

friend

◆ sample_between [3/3]

template<typename Number >

template<typename Num >

Num sample_between	(	const Num &	lower,
		const IntRepRealAlgebraicNumber< Num > &	upper
	)

friend

◆ sgn

template<typename Number >

template<typename Num >

Sign sgn	(	const IntRepRealAlgebraicNumber< Num > &	n,
		const UnivariatePolynomial< Num > &	p
	)

friend

Field Documentation

◆ auxVariable

template<typename Number >

const Variable carl::IntRepRealAlgebraicNumber< Number >::auxVariable = fresh_real_variable("__r")

staticprivate

Definition at line 26 of file Ran.h.

◆ m_content

template<typename Number >

std::shared_ptr<content> carl::IntRepRealAlgebraicNumber< Number >::m_content

mutableprivate

Definition at line 87 of file Ran.h.

The documentation for this class was generated from the following files:

carl-arith/poly/umvpoly/UnivariatePolynomial.h
carl-arith/ran/interval/Ran.h

Data Structures

Public Member Functions

Static Public Member Functions

Private Member Functions

Static Private Member Functions

Private Attributes

Static Private Attributes

Friends

Detailed Description

template<typename Number> class carl::IntRepRealAlgebraicNumber< Number >

Constructor & Destructor Documentation

◆ IntRepRealAlgebraicNumber() [1/5]

◆ IntRepRealAlgebraicNumber() [2/5]

◆ IntRepRealAlgebraicNumber() [3/5]

◆ IntRepRealAlgebraicNumber() [4/5]

◆ IntRepRealAlgebraicNumber() [5/5]

Member Function Documentation

◆ create_safe()

◆ interval()

◆ interval_int()

◆ is_consistent()

◆ is_numeric()

◆ operator=() [1/2]

◆ operator=() [2/2]

◆ polynomial()

◆ polynomial_int()

◆ refine()

◆ refine_internal()

◆ refine_to_integrality()

◆ refine_using()

◆ replace_variable()

◆ set_polynomial()

◆ value()

Friends And Related Function Documentation

◆ branching_point

◆ ceil

◆ compare [1/2]

◆ compare [2/2]

◆ evaluate [1/2]

◆ evaluate [2/2]

◆ floor

◆ sample_above

◆ sample_below

◆ sample_between [1/3]

◆ sample_between [2/3]

◆ sample_between [3/3]

◆ sgn

Field Documentation

◆ auxVariable

◆ m_content

template<typename Number>
class carl::IntRepRealAlgebraicNumber< Number >