This class represents a univariate polynomial with coefficients of an arbitrary type. More...
#include <UnivariatePolynomial.h>
Public Types | |
| using | NumberType = typename UnderlyingNumberType< Coefficient >::type |
| The number type that is ultimately used for the coefficients. More... | |
| using | IntNumberType = typename IntegralType< NumberType >::type |
| The integral type that belongs to the number type. More... | |
| using | CACHE = void |
| using | CoeffType = Coefficient |
| using | PolyType = UnivariatePolynomial< Coefficient > |
| using | RootType = IntRepRealAlgebraicNumber< NumberType > |
Public Member Functions | |
| UnivariatePolynomial ()=delete | |
| Default constructor shall not exist. More... | |
| UnivariatePolynomial (const UnivariatePolynomial &p) | |
| Copy constructor. More... | |
| UnivariatePolynomial (UnivariatePolynomial &&p) noexcept | |
| Move constructor. More... | |
| UnivariatePolynomial & | operator= (const UnivariatePolynomial &p) |
| Copy assignment operator. More... | |
| UnivariatePolynomial & | operator= (UnivariatePolynomial &&p) noexcept |
| Move assignment operator. More... | |
| UnivariatePolynomial (Variable mainVar) | |
| Construct a zero polynomial with the given main variable. More... | |
| UnivariatePolynomial (Variable mainVar, const Coefficient &coeff, std::size_t degree=0) | |
| Construct | |
| UnivariatePolynomial (Variable mainVar, std::initializer_list< Coefficient > coefficients) | |
| Construct polynomial with the given coefficients. More... | |
| template<typename C = Coefficient, DisableIf< std::is_same< C, typename UnderlyingNumberType< C >::type >> = dummy> | |
| UnivariatePolynomial (Variable mainVar, std::initializer_list< typename UnderlyingNumberType< C >::type > coefficients) | |
| Construct polynomial with the given coefficients from the underlying number type of the coefficient type. More... | |
| UnivariatePolynomial (Variable mainVar, const std::vector< Coefficient > &coefficients) | |
| Construct polynomial with the given coefficients. More... | |
| UnivariatePolynomial (Variable mainVar, std::vector< Coefficient > &&coefficients) | |
| Construct polynomial with the given coefficients, moving the coefficients. More... | |
| UnivariatePolynomial (Variable mainVar, const std::map< uint, Coefficient > &coefficients) | |
| Construct polynomial with the given coefficients. More... | |
| ~UnivariatePolynomial ()=default | |
| Destructor. More... | |
| bool | is_zero () const |
| Checks if the polynomial is equal to zero. More... | |
| bool | is_one () const |
| Checks if the polynomial is equal to one. More... | |
| UnivariatePolynomial | one () const |
| Creates a polynomial of value one with the same main variable. More... | |
| const Coefficient & | lcoeff () const |
| Returns the leading coefficient. More... | |
| const Coefficient & | tcoeff () const |
| Returns the trailing coefficient. More... | |
| bool | is_constant () const |
| Checks whether the polynomial is constant with respect to the main variable. More... | |
| bool | is_linear_in_main_var () const |
| bool | is_number () const |
| Checks whether the polynomial is only a number. More... | |
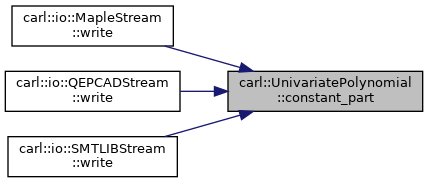
| NumberType | constant_part () const |
| Returns the constant part of this polynomial. More... | |
| bool | is_univariate () const |
| Checks if the polynomial is univariate, that means if only one variable occurs. More... | |
| uint | degree () const |
| Get the maximal exponent of the main variable. More... | |
| uint | total_degree () const |
| Returns the total degree of the polynomial, that is the maximum degree of any monomial. More... | |
| void | truncate () |
| Removes the leading term from the polynomial. More... | |
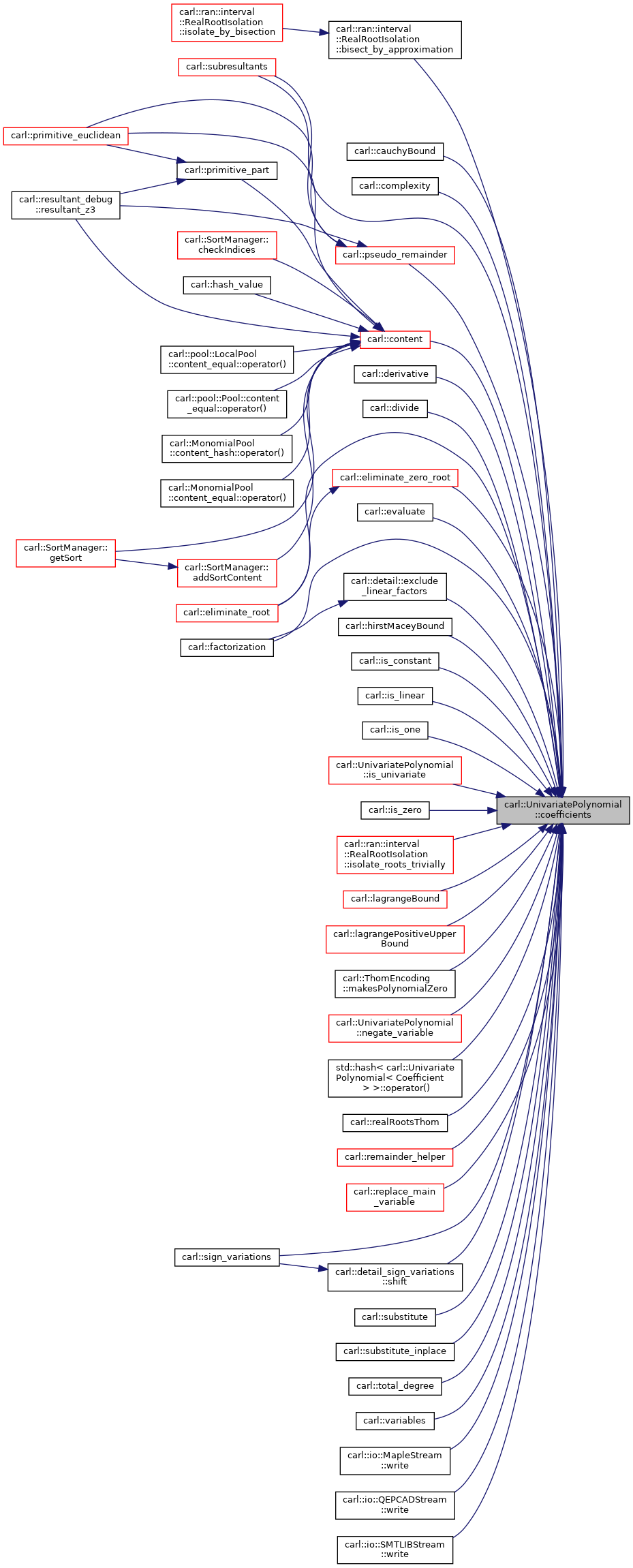
| const std::vector< Coefficient > & | coefficients () const & |
| Retrieves the coefficients defining this polynomial. More... | |
| std::vector< Coefficient > & | coefficients () & |
| Returns the coefficients as non-const reference. More... | |
| std::vector< Coefficient > && | coefficients () && |
| Returns the coefficients as rvalue. The polynomial may be in an undefined state afterwards! More... | |
| Variable | main_var () const |
| Retrieves the main variable of this polynomial. More... | |
| bool | has (Variable v) const |
| Checks if the given variable occurs in the polynomial. More... | |
| template<typename C = Coefficient, EnableIf< is_subset_of_rationals_type< C >> = dummy> | |
| Coefficient | coprime_factor () const |
| Calculates a factor that would make the coefficients of this polynomial coprime integers. More... | |
| template<typename C = Coefficient, DisableIf< is_subset_of_rationals_type< C >> = dummy> | |
| UnderlyingNumberType< Coefficient >::type | coprime_factor () const |
| template<typename C = Coefficient, EnableIf< is_subset_of_rationals_type< C >> = dummy> | |
| UnivariatePolynomial< typename IntegralType< Coefficient >::type > | coprime_coefficients () const |
| Constructs a new polynomial that is scaled such that the coefficients are coprime. More... | |
| template<typename C = Coefficient, DisableIf< is_subset_of_rationals_type< C >> = dummy> | |
| UnivariatePolynomial< Coefficient > | coprime_coefficients () const |
| template<typename C = Coefficient, EnableIf< is_subset_of_rationals_type< C >> = dummy> | |
| UnivariatePolynomial< typename IntegralType< Coefficient >::type > | coprime_coefficients_sign_preserving () const |
| template<typename C = Coefficient, DisableIf< is_subset_of_rationals_type< C >> = dummy> | |
| UnivariatePolynomial< Coefficient > | coprime_coefficients_sign_preserving () const |
| bool | is_normal () const |
| Checks whether the polynomial is unit normal. More... | |
| UnivariatePolynomial | normalized () const |
| The normal part of a polynomial is the polynomial divided by the unit part. More... | |
| Coefficient | unit_part () const |
| The unit part of a polynomial over a field is its leading coefficient for nonzero polynomials, and one for zero polynomials. More... | |
| UnivariatePolynomial | negate_variable () const |
Constructs a new polynomial q such that p is this polynomial. More... | |
| UnivariatePolynomial | reverse_coefficients () const |
| Reverse coefficients safely. More... | |
| bool | divides (const UnivariatePolynomial &divisor) const |
| Checks if this polynomial is divisible by the given divisor, that is if the remainder is zero. More... | |
| UnivariatePolynomial & | mod (const Coefficient &modulus) |
Replaces every coefficient c by c mod modulus. More... | |
| UnivariatePolynomial | mod (const Coefficient &modulus) const |
Constructs a new polynomial where every coefficient c is replaced by c mod modulus. More... | |
| UnivariatePolynomial | pow (std::size_t exp) const |
| Returns this polynomial to the given power. More... | |
| Coefficient | evaluate (const Coefficient &value) const |
| carl::Sign | sgn (const Coefficient &value) const |
| Calculates the sign of the polynomial at some point. More... | |
| template<typename SubstitutionType , typename C = Coefficient, EnableIf< is_instantiation_of< MultivariatePolynomial, C >> = dummy> | |
| UnivariatePolynomial< Coefficient > | evaluateCoefficient (const std::map< Variable, SubstitutionType > &) const |
| template<typename SubstitutionType , typename C = Coefficient, DisableIf< is_instantiation_of< MultivariatePolynomial, C >> = dummy> | |
| UnivariatePolynomial< Coefficient > | evaluateCoefficient (const std::map< Variable, SubstitutionType > &) const |
| template<typename T = Coefficient, EnableIf< has_normalize< T >> = dummy> | |
| UnivariatePolynomial & | normalizeCoefficients () |
| template<typename T = Coefficient, DisableIf< has_normalize< T >> = dummy> | |
| UnivariatePolynomial & | normalizeCoefficients () |
| template<typename C = Coefficient, EnableIf< is_instantiation_of< GFNumber, C >> = dummy> | |
| UnivariatePolynomial< typename IntegralType< Coefficient >::type > | to_integer_domain () const |
| Works only from rationals, if the numbers are already integers. More... | |
| template<typename C = Coefficient, DisableIf< is_instantiation_of< GFNumber, C >> = dummy> | |
| UnivariatePolynomial< typename IntegralType< Coefficient >::type > | to_integer_domain () const |
| UnivariatePolynomial< GFNumber< typename IntegralType< Coefficient >::type > > | toFiniteDomain (const GaloisField< typename IntegralType< Coefficient >::type > *galoisField) const |
| template<typename C = Coefficient, DisableIf< is_number_type< C >> = dummy> | |
| UnivariatePolynomial< NumberType > | toNumberCoefficients () const |
| Asserts that is_univariate() is true. More... | |
| template<typename NewCoeff > | |
| UnivariatePolynomial< NewCoeff > | convert () const |
| template<typename NewCoeff > | |
| UnivariatePolynomial< NewCoeff > | convert (const std::function< NewCoeff(const Coefficient &)> &f) const |
| NumberType | numeric_content (std::size_t i) const |
| Returns the numeric content part of the i'th coefficient. More... | |
| NumberType | numeric_unit () const |
| Returns the numeric unit part of the polynomial. More... | |
| template<typename N = NumberType, EnableIf< is_subset_of_rationals_type< N >> = dummy> | |
| UnderlyingNumberType< Coefficient >::type | numeric_content () const |
| Obtains the numeric content part of this polynomial. More... | |
| template<typename C = Coefficient, EnableIf< is_number_type< C >> = dummy> | |
| IntNumberType | main_denom () const |
| Compute the main denominator of all numeric coefficients of this polynomial. More... | |
| template<typename C = Coefficient, DisableIf< is_number_type< C >> = dummy> | |
| IntNumberType | main_denom () const |
| Coefficient | synthetic_division (const Coefficient &zeroOfDivisor) |
| bool | zero_is_root () const |
| Checks if zero is a real root of this polynomial. More... | |
| bool | less (const UnivariatePolynomial< Coefficient > &rhs, const PolynomialComparisonOrder &order=PolynomialComparisonOrder::Default) const |
| UnivariatePolynomial | operator- () const |
| template<typename C = Coefficient, EnableIf< is_number_type< C >> = dummy> | |
| bool | is_consistent () const |
| Asserts that this polynomial over numeric coefficients complies with the requirements and assumptions for UnivariatePolynomial objects. More... | |
| template<typename C = Coefficient, DisableIf< is_number_type< C >> = dummy> | |
| bool | is_consistent () const |
| Asserts that this polynomial over polynomial coefficients complies with the requirements and assumptions for UnivariatePolynomial objects. More... | |
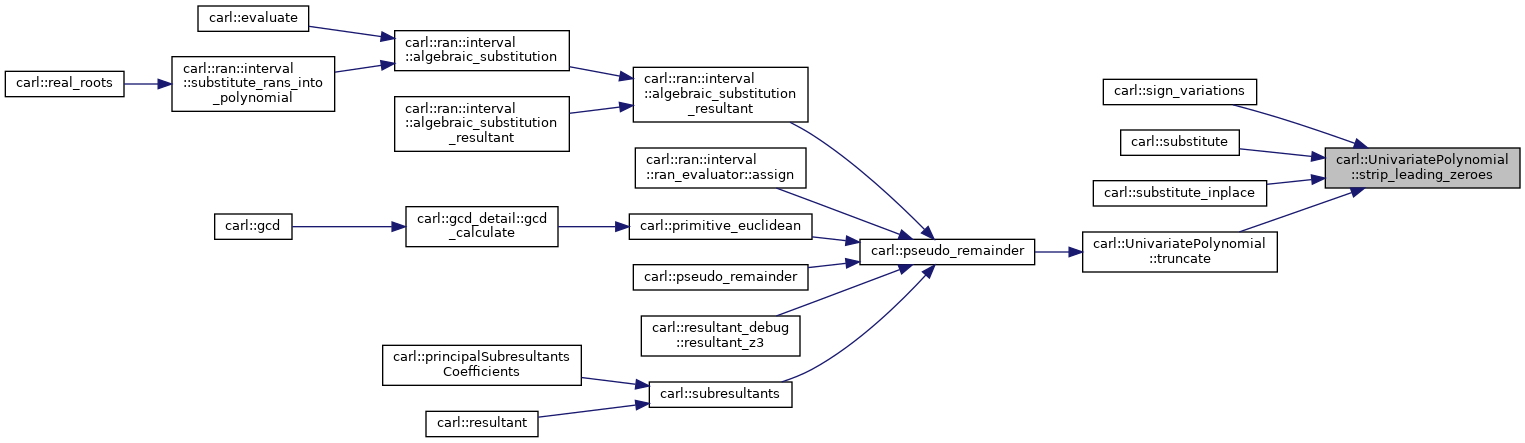
| void | strip_leading_zeroes () |
In-place addition operators | |
| UnivariatePolynomial & | operator+= (const Coefficient &rhs) |
| Add something to this polynomial and return the changed polynomial. More... | |
| UnivariatePolynomial & | operator+= (const UnivariatePolynomial &rhs) |
| Add something to this polynomial and return the changed polynomial. More... | |
In-place subtraction operators | |
| UnivariatePolynomial & | operator-= (const Coefficient &rhs) |
| Subtract something from this polynomial and return the changed polynomial. More... | |
| UnivariatePolynomial & | operator-= (const UnivariatePolynomial &rhs) |
| Subtract something from this polynomial and return the changed polynomial. More... | |
In-place multiplication operators | |
| template<typename C = Coefficient, EnableIf< is_number_type< C >> = dummy> | |
| UnivariatePolynomial & | operator*= (Variable rhs) |
| Multiply this polynomial with something and return the changed polynomial. More... | |
| template<typename C = Coefficient, DisableIf< is_number_type< C >> = dummy> | |
| UnivariatePolynomial & | operator*= (Variable rhs) |
| Multiply this polynomial with something and return the changed polynomial. More... | |
| UnivariatePolynomial & | operator*= (const Coefficient &rhs) |
| Multiply this polynomial with something and return the changed polynomial. More... | |
| template<typename I = Coefficient, DisableIf< std::is_same< Coefficient, I >> ...> | |
| UnivariatePolynomial & | operator*= (const typename IntegralType< Coefficient >::type &rhs) |
| Multiply this polynomial with something and return the changed polynomial. More... | |
| UnivariatePolynomial & | operator*= (const UnivariatePolynomial &rhs) |
| Multiply this polynomial with something and return the changed polynomial. More... | |
In-place division operators | |
| template<typename C = Coefficient, EnableIf< is_field_type< C >> = dummy> | |
| UnivariatePolynomial & | operator/= (const Coefficient &rhs) |
| Divide this polynomial by something and return the changed polynomial. More... | |
| template<typename C = Coefficient, DisableIf< is_field_type< C >> = dummy> | |
| UnivariatePolynomial & | operator/= (const Coefficient &rhs) |
| Divide this polynomial by something and return the changed polynomial. More... | |
Private Attributes | |
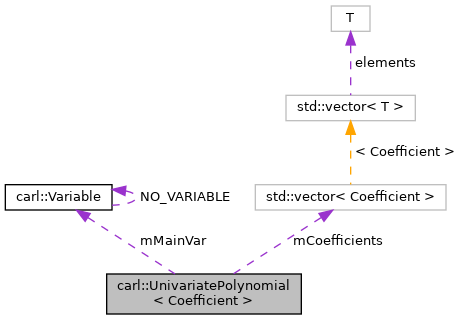
| Variable | mMainVar |
| The main variable. More... | |
| std::vector< Coefficient > | mCoefficients |
| The coefficients. More... | |
Friends | |
| template<class T > | |
| class | UnivariatePolynomial |
| Declare all instantiations of univariate polynomials as friends. More... | |
| template<typename C > | |
| bool | operator< (const UnivariatePolynomial< C > &lhs, const UnivariatePolynomial< C > &rhs) |
| template<typename C > | |
| std::ostream & | operator<< (std::ostream &os, const UnivariatePolynomial< C > &rhs) |
| Streaming operator for univariate polynomials. More... | |
Equality comparison operators | |
| template<typename C > | |
| bool | operator== (const C &lhs, const UnivariatePolynomial< C > &rhs) |
| Checks if the two arguments are equal. More... | |
| template<typename C > | |
| bool | operator== (const UnivariatePolynomial< C > &lhs, const C &rhs) |
| Checks if the two arguments are equal. More... | |
| template<typename C > | |
| bool | operator== (const UnivariatePolynomial< C > &lhs, const UnivariatePolynomial< C > &rhs) |
| Checks if the two arguments are equal. More... | |
| template<typename C > | |
| bool | operator== (const UnivariatePolynomialPtr< C > &lhs, const UnivariatePolynomialPtr< C > &rhs) |
| Checks if the two arguments are equal. More... | |
Inequality comparison operators | |
| template<typename C > | |
| bool | operator!= (const UnivariatePolynomial< C > &lhs, const UnivariatePolynomial< C > &rhs) |
| Checks if the two arguments are not equal. More... | |
| template<typename C > | |
| bool | operator!= (const UnivariatePolynomialPtr< C > &lhs, const UnivariatePolynomialPtr< C > &rhs) |
| Checks if the two arguments are not equal. More... | |
Addition operators | |
| template<typename C > | |
| UnivariatePolynomial< C > | operator+ (const UnivariatePolynomial< C > &lhs, const UnivariatePolynomial< C > &rhs) |
| Performs an addition involving a polynomial. More... | |
| template<typename C > | |
| UnivariatePolynomial< C > | operator+ (const C &lhs, const UnivariatePolynomial< C > &rhs) |
| Performs an addition involving a polynomial. More... | |
| template<typename C > | |
| UnivariatePolynomial< C > | operator+ (const UnivariatePolynomial< C > &lhs, const C &rhs) |
| Performs an addition involving a polynomial. More... | |
Subtraction operators | |
| template<typename C > | |
| UnivariatePolynomial< C > | operator- (const UnivariatePolynomial< C > &lhs, const UnivariatePolynomial< C > &rhs) |
| Performs a subtraction involving a polynomial. More... | |
| template<typename C > | |
| UnivariatePolynomial< C > | operator- (const C &lhs, const UnivariatePolynomial< C > &rhs) |
| Performs a subtraction involving a polynomial. More... | |
| template<typename C > | |
| UnivariatePolynomial< C > | operator- (const UnivariatePolynomial< C > &lhs, const C &rhs) |
| Performs a subtraction involving a polynomial. More... | |
Multiplication operators | |
| template<typename C > | |
| UnivariatePolynomial< C > | operator* (const UnivariatePolynomial< C > &lhs, const UnivariatePolynomial< C > &rhs) |
| Perform a multiplication involving a polynomial. More... | |
| template<typename C > | |
| UnivariatePolynomial< C > | operator* (const UnivariatePolynomial< C > &lhs, Variable rhs) |
| Perform a multiplication involving a polynomial. More... | |
| template<typename C > | |
| UnivariatePolynomial< C > | operator* (Variable lhs, const UnivariatePolynomial< C > &rhs) |
| Perform a multiplication involving a polynomial. More... | |
| template<typename C > | |
| UnivariatePolynomial< C > | operator* (const C &lhs, const UnivariatePolynomial< C > &rhs) |
| Perform a multiplication involving a polynomial. More... | |
| template<typename C > | |
| UnivariatePolynomial< C > | operator* (const UnivariatePolynomial< C > &lhs, const C &rhs) |
| Perform a multiplication involving a polynomial. More... | |
| template<typename C > | |
| UnivariatePolynomial< C > | operator* (const IntegralTypeIfDifferent< C > &lhs, const UnivariatePolynomial< C > &rhs) |
| Perform a multiplication involving a polynomial. More... | |
| template<typename C > | |
| UnivariatePolynomial< C > | operator* (const UnivariatePolynomial< C > &lhs, const IntegralTypeIfDifferent< C > &rhs) |
| Perform a multiplication involving a polynomial. More... | |
| template<typename C , typename O , typename P > | |
| UnivariatePolynomial< MultivariatePolynomial< C, O, P > > | operator* (const UnivariatePolynomial< MultivariatePolynomial< C, O, P >> &lhs, const C &rhs) |
| Perform a multiplication involving a polynomial. More... | |
| template<typename C , typename O , typename P > | |
| UnivariatePolynomial< MultivariatePolynomial< C, O, P > > | operator* (const C &lhs, const UnivariatePolynomial< MultivariatePolynomial< C, O, P >> &rhs) |
| Perform a multiplication involving a polynomial. More... | |
Division operators | |
| template<typename C > | |
| UnivariatePolynomial< C > | operator/ (const UnivariatePolynomial< C > &lhs, const C &rhs) |
| Perform a division involving a polynomial. More... | |
Detailed Description
template<typename Coefficient>
class carl::UnivariatePolynomial< Coefficient >
This class represents a univariate polynomial with coefficients of an arbitrary type.
A univariate polynomial is defined by a variable (the main variable) and the coefficients. The coefficients may be of any type. The intention is to use a numbers or polynomials as coefficients. If polynomials are used as coefficients, this can be seen as a multivariate polynomial with a distinguished main variable.
Most methods are specifically adapted for polynomial coefficients, if necessary.
Definition at line 61 of file UnivariatePolynomial.h.
Member Typedef Documentation
◆ CACHE
| using carl::UnivariatePolynomial< Coefficient >::CACHE = void |
Definition at line 83 of file UnivariatePolynomial.h.
◆ CoeffType
| using carl::UnivariatePolynomial< Coefficient >::CoeffType = Coefficient |
Definition at line 84 of file UnivariatePolynomial.h.
◆ IntNumberType
| using carl::UnivariatePolynomial< Coefficient >::IntNumberType = typename IntegralType<NumberType>::type |
The integral type that belongs to the number type.
Definition at line 81 of file UnivariatePolynomial.h.
◆ NumberType
| using carl::UnivariatePolynomial< Coefficient >::NumberType = typename UnderlyingNumberType<Coefficient>::type |
The number type that is ultimately used for the coefficients.
Definition at line 77 of file UnivariatePolynomial.h.
◆ PolyType
| using carl::UnivariatePolynomial< Coefficient >::PolyType = UnivariatePolynomial<Coefficient> |
Definition at line 85 of file UnivariatePolynomial.h.
◆ RootType
| using carl::UnivariatePolynomial< Coefficient >::RootType = IntRepRealAlgebraicNumber<NumberType> |
Definition at line 86 of file UnivariatePolynomial.h.
Constructor & Destructor Documentation
◆ UnivariatePolynomial() [1/10]
|
delete |
Default constructor shall not exist.
Use UnivariatePolynomial(Variable) instead.
◆ UnivariatePolynomial() [2/10]
| carl::UnivariatePolynomial< Coefficient >::UnivariatePolynomial | ( | const UnivariatePolynomial< Coefficient > & | p | ) |
Copy constructor.
◆ UnivariatePolynomial() [3/10]
|
noexcept |
Move constructor.
◆ UnivariatePolynomial() [4/10]
|
explicit |
Construct a zero polynomial with the given main variable.
- Parameters
-
mainVar New main variable.
◆ UnivariatePolynomial() [5/10]
| carl::UnivariatePolynomial< Coefficient >::UnivariatePolynomial | ( | Variable | mainVar, |
| const Coefficient & | coeff, | ||
| std::size_t | degree = 0 |
||
| ) |
Construct ![]() .
.
- Parameters
-
mainVar New main variable. coeff Leading coefficient. degree Degree.
◆ UnivariatePolynomial() [6/10]
| carl::UnivariatePolynomial< Coefficient >::UnivariatePolynomial | ( | Variable | mainVar, |
| std::initializer_list< Coefficient > | coefficients | ||
| ) |
Construct polynomial with the given coefficients.
- Parameters
-
mainVar New main variable. coefficients List of coefficients.
◆ UnivariatePolynomial() [7/10]
| carl::UnivariatePolynomial< Coefficient >::UnivariatePolynomial | ( | Variable | mainVar, |
| std::initializer_list< typename UnderlyingNumberType< C >::type > | coefficients | ||
| ) |
Construct polynomial with the given coefficients from the underlying number type of the coefficient type.
- Parameters
-
mainVar New main variable. coefficients List of coefficients.
◆ UnivariatePolynomial() [8/10]
| carl::UnivariatePolynomial< Coefficient >::UnivariatePolynomial | ( | Variable | mainVar, |
| const std::vector< Coefficient > & | coefficients | ||
| ) |
Construct polynomial with the given coefficients.
- Parameters
-
mainVar New main variable. coefficients Vector of coefficients.
◆ UnivariatePolynomial() [9/10]
| carl::UnivariatePolynomial< Coefficient >::UnivariatePolynomial | ( | Variable | mainVar, |
| std::vector< Coefficient > && | coefficients | ||
| ) |
Construct polynomial with the given coefficients, moving the coefficients.
- Parameters
-
mainVar New main variable. coefficients Vector of coefficients.
◆ UnivariatePolynomial() [10/10]
| carl::UnivariatePolynomial< Coefficient >::UnivariatePolynomial | ( | Variable | mainVar, |
| const std::map< uint, Coefficient > & | coefficients | ||
| ) |
Construct polynomial with the given coefficients.
- Parameters
-
mainVar New main variable. coefficients Assignment of degree to coefficients.
◆ ~UnivariatePolynomial()
|
default |
Destructor.
Member Function Documentation
◆ coefficients() [1/3]
|
inline |
Returns the coefficients as non-const reference.
Definition at line 329 of file UnivariatePolynomial.h.
◆ coefficients() [2/3]
|
inline |
Returns the coefficients as rvalue. The polynomial may be in an undefined state afterwards!
Definition at line 333 of file UnivariatePolynomial.h.
◆ coefficients() [3/3]
|
inline |
Retrieves the coefficients defining this polynomial.
- Returns
- Coefficients.
Definition at line 325 of file UnivariatePolynomial.h.
◆ constant_part()
|
inline |
Returns the constant part of this polynomial.
- Returns
- Constant part.
Definition at line 253 of file UnivariatePolynomial.h.

◆ convert() [1/2]
| UnivariatePolynomial<NewCoeff> carl::UnivariatePolynomial< Coefficient >::convert | ( | ) | const |

◆ convert() [2/2]
| UnivariatePolynomial<NewCoeff> carl::UnivariatePolynomial< Coefficient >::convert | ( | const std::function< NewCoeff(const Coefficient &)> & | f | ) | const |
◆ coprime_coefficients() [1/2]
| UnivariatePolynomial<typename IntegralType<Coefficient>::type> carl::UnivariatePolynomial< Coefficient >::coprime_coefficients | ( | ) | const |
Constructs a new polynomial that is scaled such that the coefficients are coprime.
It is calculated by multiplying it with the coprime factor. By definition, this results in a polynomial with integral coefficients.
- Returns
- This polynomial multiplied with the coprime factor.

◆ coprime_coefficients() [2/2]
| UnivariatePolynomial<Coefficient> carl::UnivariatePolynomial< Coefficient >::coprime_coefficients | ( | ) | const |
◆ coprime_coefficients_sign_preserving() [1/2]
| UnivariatePolynomial<typename IntegralType<Coefficient>::type> carl::UnivariatePolynomial< Coefficient >::coprime_coefficients_sign_preserving | ( | ) | const |
◆ coprime_coefficients_sign_preserving() [2/2]
| UnivariatePolynomial<Coefficient> carl::UnivariatePolynomial< Coefficient >::coprime_coefficients_sign_preserving | ( | ) | const |
◆ coprime_factor() [1/2]
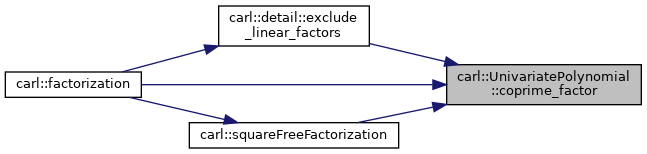
| Coefficient carl::UnivariatePolynomial< Coefficient >::coprime_factor | ( | ) | const |
Calculates a factor that would make the coefficients of this polynomial coprime integers.
We consider a set of integers coprime, if they share no common factor. Technically, the coprime factor is ![]() where
where N is the set of the numerators and D is the set of the denominators of all coefficients.
- Returns
- Coprime factor of this polynomial.
◆ coprime_factor() [2/2]
| UnderlyingNumberType<Coefficient>::type carl::UnivariatePolynomial< Coefficient >::coprime_factor | ( | ) | const |
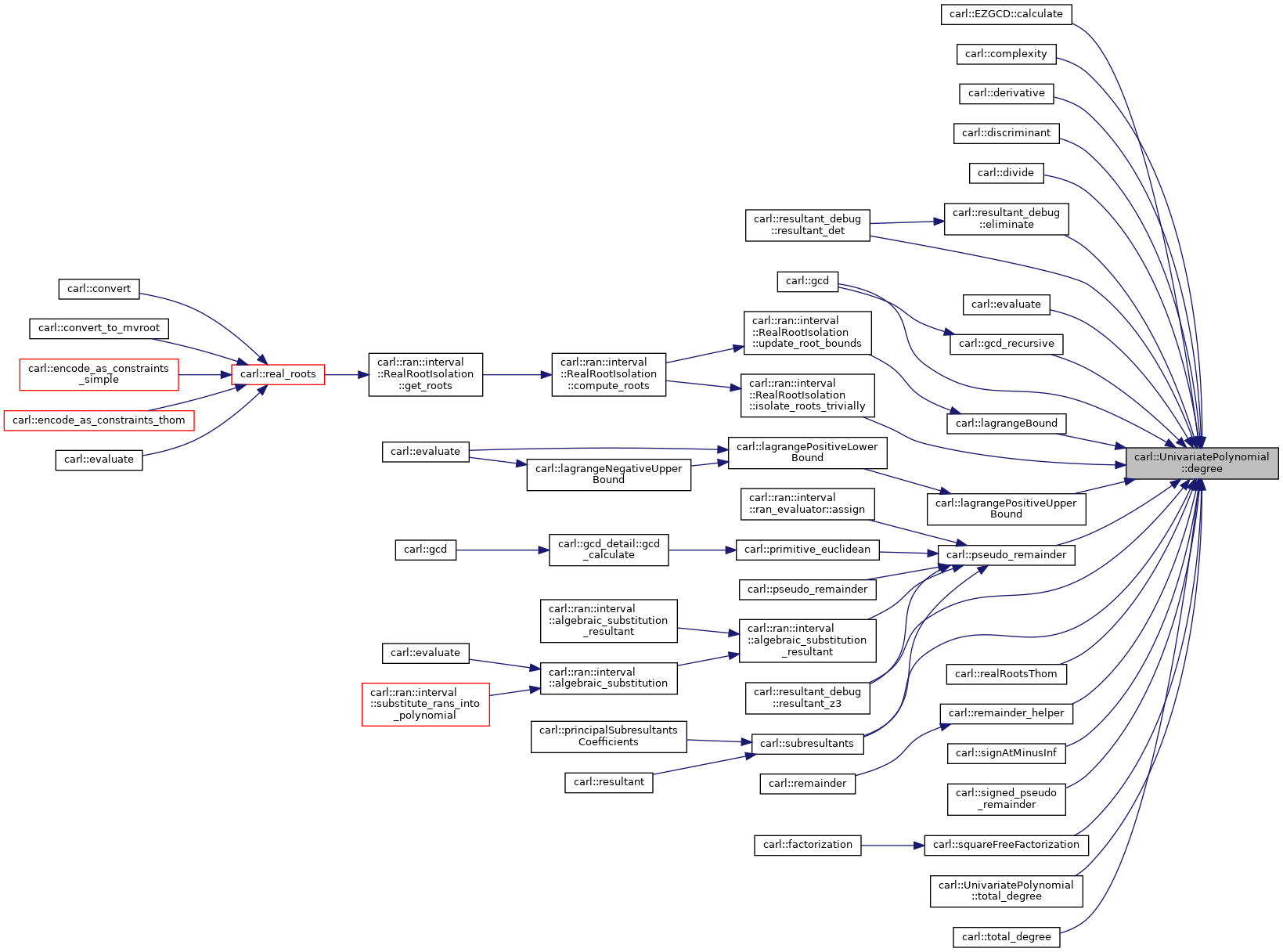
◆ degree()
|
inline |
Get the maximal exponent of the main variable.
As the degree of the zero polynomial is ![]() , we assert that this polynomial is not zero. This must be checked by the caller before calling this method.
, we assert that this polynomial is not zero. This must be checked by the caller before calling this method.
- See also
- [3], page 38
- Returns
- Degree.
Definition at line 284 of file UnivariatePolynomial.h.
◆ divides()
| bool carl::UnivariatePolynomial< Coefficient >::divides | ( | const UnivariatePolynomial< Coefficient > & | divisor | ) | const |
Checks if this polynomial is divisible by the given divisor, that is if the remainder is zero.
- Parameters
-
divisor Polynomial.
- Returns
- If divisor divides this polynomial.
◆ evaluate()
| Coefficient carl::UnivariatePolynomial< Coefficient >::evaluate | ( | const Coefficient & | value | ) | const |

◆ evaluateCoefficient() [1/2]
|
inline |
◆ evaluateCoefficient() [2/2]
|
inline |
Definition at line 487 of file UnivariatePolynomial.h.
◆ has()
|
inline |
Checks if the given variable occurs in the polynomial.
- Parameters
-
v Variable.
- Returns
- If v occurs in the polynomial.
Definition at line 350 of file UnivariatePolynomial.h.


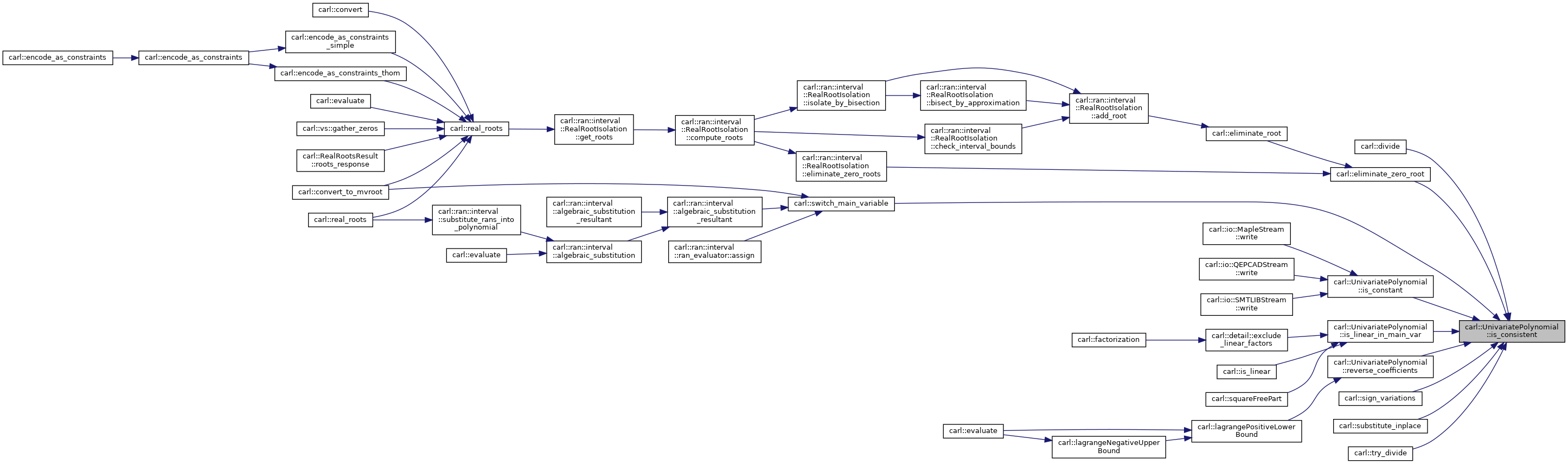
◆ is_consistent() [1/2]
| bool carl::UnivariatePolynomial< Coefficient >::is_consistent | ( | ) | const |
Asserts that this polynomial over numeric coefficients complies with the requirements and assumptions for UnivariatePolynomial objects.
- The leading term is not zero.
◆ is_consistent() [2/2]
| bool carl::UnivariatePolynomial< Coefficient >::is_consistent | ( | ) | const |
Asserts that this polynomial over polynomial coefficients complies with the requirements and assumptions for UnivariatePolynomial objects.
- The leading term is not zero.
- The main variable does not occur in any coefficient.
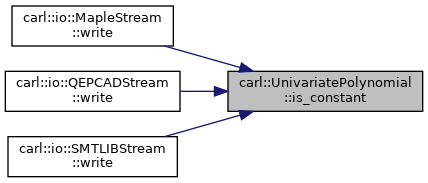
◆ is_constant()
|
inline |
Checks whether the polynomial is constant with respect to the main variable.
- Returns
- If polynomial is constant.
Definition at line 223 of file UnivariatePolynomial.h.

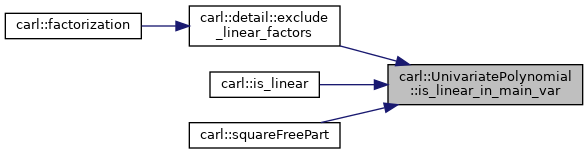
◆ is_linear_in_main_var()
|
inline |
Definition at line 229 of file UnivariatePolynomial.h.

◆ is_normal()
| bool carl::UnivariatePolynomial< Coefficient >::is_normal | ( | ) | const |
Checks whether the polynomial is unit normal.
A polynomial is unit normal, if the leading coefficient is unit normal, that is if it is either one or minus one.
- See also
- [3], page 39
- Returns
- If polynomial is normal.

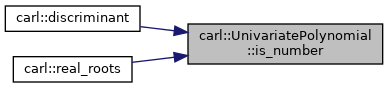
◆ is_number()
|
inline |
Checks whether the polynomial is only a number.
- Returns
- If polynomial is a number.
Definition at line 239 of file UnivariatePolynomial.h.

◆ is_one()
|
inline |
Checks if the polynomial is equal to one.
- Returns
- If polynomial is one.
Definition at line 177 of file UnivariatePolynomial.h.

◆ is_univariate()
|
inline |
Checks if the polynomial is univariate, that means if only one variable occurs.
- Returns
- true.
Definition at line 267 of file UnivariatePolynomial.h.


◆ is_zero()
|
inline |
Checks if the polynomial is equal to zero.
- Returns
- If polynomial is zero.
Definition at line 167 of file UnivariatePolynomial.h.

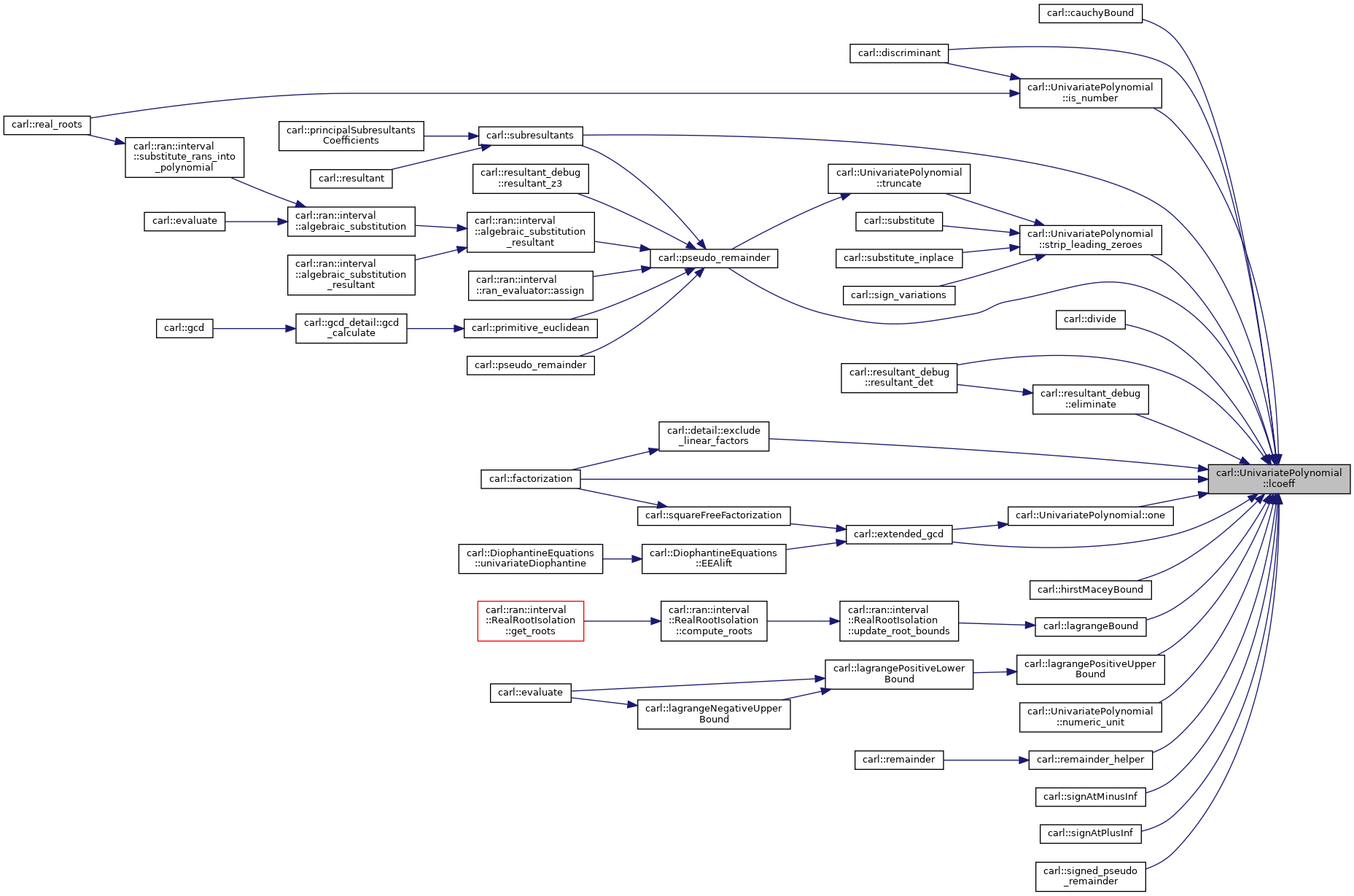
◆ lcoeff()
|
inline |
Returns the leading coefficient.
Asserts, that the polynomial is not empty.
- Returns
- The leading coefficient.
Definition at line 203 of file UnivariatePolynomial.h.
◆ less()
| bool carl::UnivariatePolynomial< Coefficient >::less | ( | const UnivariatePolynomial< Coefficient > & | rhs, |
| const PolynomialComparisonOrder & | order = PolynomialComparisonOrder::Default |
||
| ) | const |

◆ main_denom() [1/2]
| IntNumberType carl::UnivariatePolynomial< Coefficient >::main_denom | ( | ) | const |
Compute the main denominator of all numeric coefficients of this polynomial.
This method only applies if the Coefficient type is a number.
- Returns
- the main denominator of all coefficients of this polynomial.
◆ main_denom() [2/2]
| IntNumberType carl::UnivariatePolynomial< Coefficient >::main_denom | ( | ) | const |
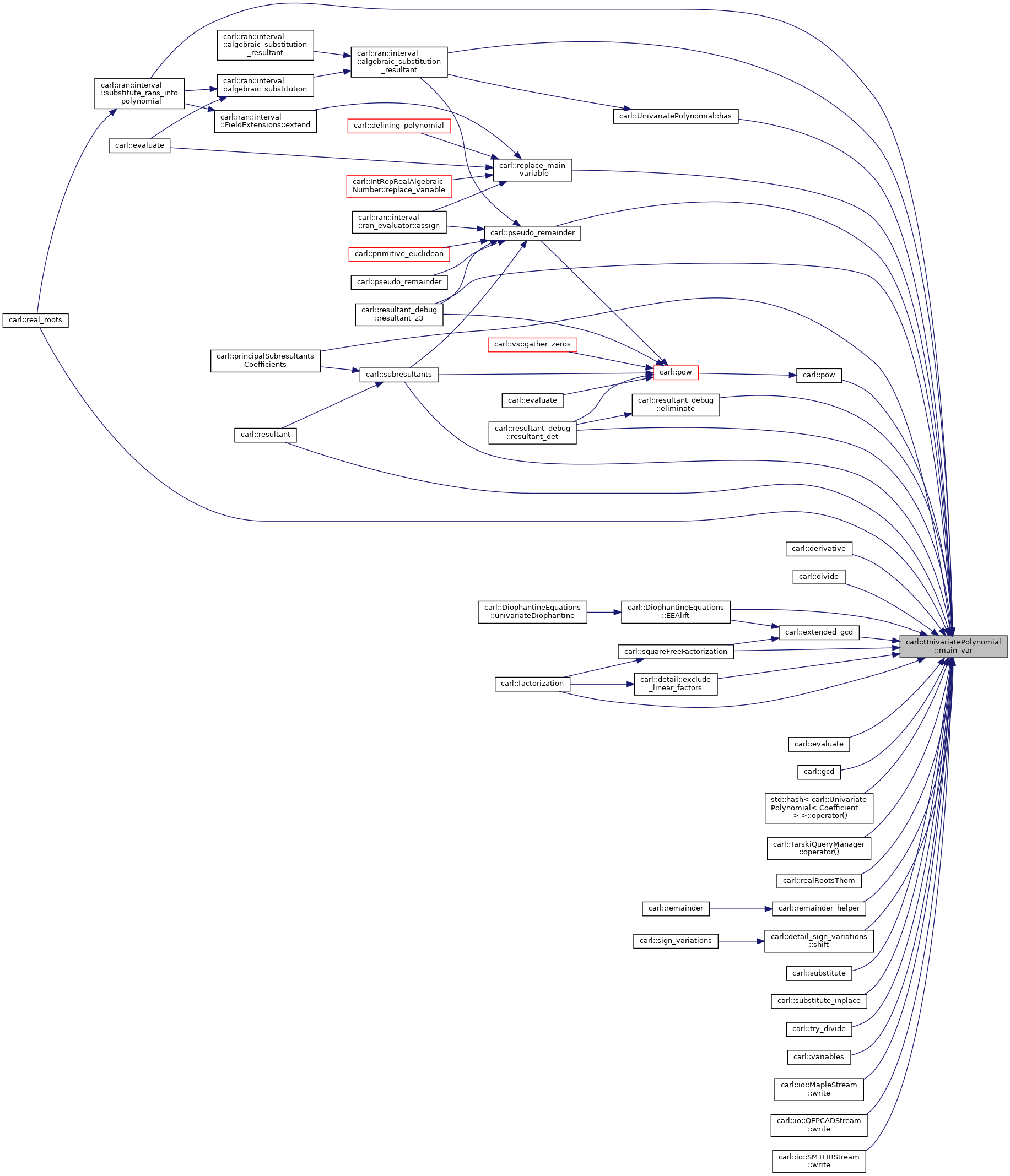
◆ main_var()
|
inline |
Retrieves the main variable of this polynomial.
- Returns
- Main variable.
Definition at line 341 of file UnivariatePolynomial.h.
◆ mod() [1/2]
| UnivariatePolynomial& carl::UnivariatePolynomial< Coefficient >::mod | ( | const Coefficient & | modulus | ) |
Replaces every coefficient c by c mod modulus.
- Parameters
-
modulus Modulus.
- Returns
- This.
◆ mod() [2/2]
| UnivariatePolynomial carl::UnivariatePolynomial< Coefficient >::mod | ( | const Coefficient & | modulus | ) | const |
Constructs a new polynomial where every coefficient c is replaced by c mod modulus.
- Parameters
-
modulus Modulus.
- Returns
- New polynomial.
◆ negate_variable()
|
inline |
Constructs a new polynomial q such that ![]() where
where p is this polynomial.
- Returns
- New polynomial with negated variable.
Definition at line 419 of file UnivariatePolynomial.h.

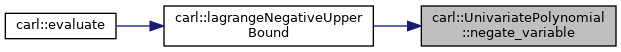
◆ normalizeCoefficients() [1/2]
|
inline |
◆ normalizeCoefficients() [2/2]
|
inline |
Definition at line 504 of file UnivariatePolynomial.h.
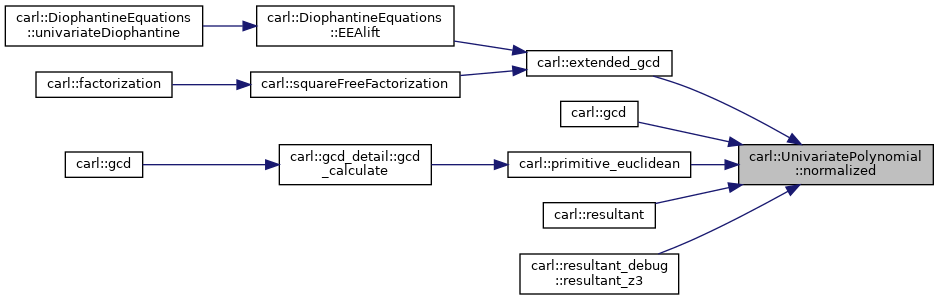
◆ normalized()
| UnivariatePolynomial carl::UnivariatePolynomial< Coefficient >::normalized | ( | ) | const |
The normal part of a polynomial is the polynomial divided by the unit part.
- See also
- [3], page 42.
- Returns
- This polynomial divided by the unit part.
◆ numeric_content() [1/2]
| UnderlyingNumberType<Coefficient>::type carl::UnivariatePolynomial< Coefficient >::numeric_content | ( | ) | const |
Obtains the numeric content part of this polynomial.
The numeric content part of a polynomial is defined as the gcd() of the numeric content parts of all coefficients. This is only possible if the underlying number type is either integral or fractional.
As for fractional numbers, we consider the following definition: gcd( a/b, c/d ) = gcd( a/b*l, c/d*l ) / l where l = lcm(b,d).
- Returns
- numeric content part of the polynomial.
- See also
- UnivariatePolynomials::numeric_content(std::size_t)
◆ numeric_content() [2/2]
|
inline |
Returns the numeric content part of the i'th coefficient.
If the coefficients are numbers, this is simply the i'th coefficient. If the coefficients are polynomials, this is the numeric content part of the i'th coefficient.
- Parameters
-
i number of the coefficient
- Returns
- numeric content part of i'th coefficient.
Definition at line 540 of file UnivariatePolynomial.h.

◆ numeric_unit()
|
inline |
Returns the numeric unit part of the polynomial.
If the coefficients are numbers, this is the sign of the leading coefficient. If the coefficients are polynomials, this is the unit part of the leading coefficient.s
- Returns
- unit part of the polynomial.
Definition at line 556 of file UnivariatePolynomial.h.

◆ one()
|
inline |
Creates a polynomial of value one with the same main variable.
- Returns
- One.
Definition at line 186 of file UnivariatePolynomial.h.


◆ operator*=() [1/5]
| UnivariatePolynomial& carl::UnivariatePolynomial< Coefficient >::operator*= | ( | const Coefficient & | rhs | ) |
Multiply this polynomial with something and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator*=() [2/5]
| UnivariatePolynomial& carl::UnivariatePolynomial< Coefficient >::operator*= | ( | const typename IntegralType< Coefficient >::type & | rhs | ) |
Multiply this polynomial with something and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator*=() [3/5]
| UnivariatePolynomial& carl::UnivariatePolynomial< Coefficient >::operator*= | ( | const UnivariatePolynomial< Coefficient > & | rhs | ) |
Multiply this polynomial with something and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator*=() [4/5]
| UnivariatePolynomial& carl::UnivariatePolynomial< Coefficient >::operator*= | ( | Variable | rhs | ) |
Multiply this polynomial with something and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator*=() [5/5]
| UnivariatePolynomial& carl::UnivariatePolynomial< Coefficient >::operator*= | ( | Variable | rhs | ) |
Multiply this polynomial with something and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator+=() [1/2]
| UnivariatePolynomial& carl::UnivariatePolynomial< Coefficient >::operator+= | ( | const Coefficient & | rhs | ) |
Add something to this polynomial and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator+=() [2/2]
| UnivariatePolynomial& carl::UnivariatePolynomial< Coefficient >::operator+= | ( | const UnivariatePolynomial< Coefficient > & | rhs | ) |
Add something to this polynomial and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator-()
| UnivariatePolynomial carl::UnivariatePolynomial< Coefficient >::operator- | ( | ) | const |
◆ operator-=() [1/2]
| UnivariatePolynomial& carl::UnivariatePolynomial< Coefficient >::operator-= | ( | const Coefficient & | rhs | ) |
Subtract something from this polynomial and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator-=() [2/2]
| UnivariatePolynomial& carl::UnivariatePolynomial< Coefficient >::operator-= | ( | const UnivariatePolynomial< Coefficient > & | rhs | ) |
Subtract something from this polynomial and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator/=() [1/2]
| UnivariatePolynomial& carl::UnivariatePolynomial< Coefficient >::operator/= | ( | const Coefficient & | rhs | ) |
Divide this polynomial by something and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator/=() [2/2]
| UnivariatePolynomial& carl::UnivariatePolynomial< Coefficient >::operator/= | ( | const Coefficient & | rhs | ) |
Divide this polynomial by something and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator=() [1/2]
| UnivariatePolynomial& carl::UnivariatePolynomial< Coefficient >::operator= | ( | const UnivariatePolynomial< Coefficient > & | p | ) |
Copy assignment operator.
◆ operator=() [2/2]
|
noexcept |
Move assignment operator.
◆ pow()
| UnivariatePolynomial carl::UnivariatePolynomial< Coefficient >::pow | ( | std::size_t | exp | ) | const |
Returns this polynomial to the given power.
- Parameters
-
exp Exponent.
- Returns
- This to the power of exp.
◆ reverse_coefficients()
|
inline |
Reverse coefficients safely.
Definition at line 430 of file UnivariatePolynomial.h.


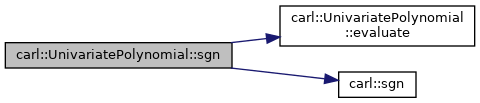
◆ sgn()
|
inline |
Calculates the sign of the polynomial at some point.
- Parameters
-
value Point to evaluate.
- Returns
- Sign at value.
Definition at line 477 of file UnivariatePolynomial.h.
◆ strip_leading_zeroes()
|
inline |
Definition at line 794 of file UnivariatePolynomial.h.

◆ synthetic_division()
| Coefficient carl::UnivariatePolynomial< Coefficient >::synthetic_division | ( | const Coefficient & | zeroOfDivisor | ) |
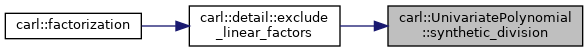
◆ tcoeff()
|
inline |
Returns the trailing coefficient.
Asserts, that the polynomial is not empty.
- Returns
- The trailing coefficient.
Definition at line 213 of file UnivariatePolynomial.h.

◆ to_integer_domain() [1/2]
| UnivariatePolynomial<typename IntegralType<Coefficient>::type> carl::UnivariatePolynomial< Coefficient >::to_integer_domain | ( | ) | const |
Works only from rationals, if the numbers are already integers.
- Returns

◆ to_integer_domain() [2/2]
| UnivariatePolynomial<typename IntegralType<Coefficient>::type> carl::UnivariatePolynomial< Coefficient >::to_integer_domain | ( | ) | const |
◆ toFiniteDomain()
| UnivariatePolynomial<GFNumber<typename IntegralType<Coefficient>::type> > carl::UnivariatePolynomial< Coefficient >::toFiniteDomain | ( | const GaloisField< typename IntegralType< Coefficient >::type > * | galoisField | ) | const |

◆ toNumberCoefficients()
| UnivariatePolynomial<NumberType> carl::UnivariatePolynomial< Coefficient >::toNumberCoefficients | ( | ) | const |
◆ total_degree()
|
inline |
Returns the total degree of the polynomial, that is the maximum degree of any monomial.
As the degree of the zero polynomial is ![]() , we assert that this polynomial is not zero. This must be checked by the caller before calling this method.
, we assert that this polynomial is not zero. This must be checked by the caller before calling this method.
- See also
- [3], page 38
- Returns
- Total degree.
Definition at line 296 of file UnivariatePolynomial.h.
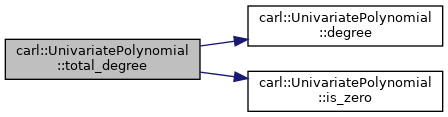
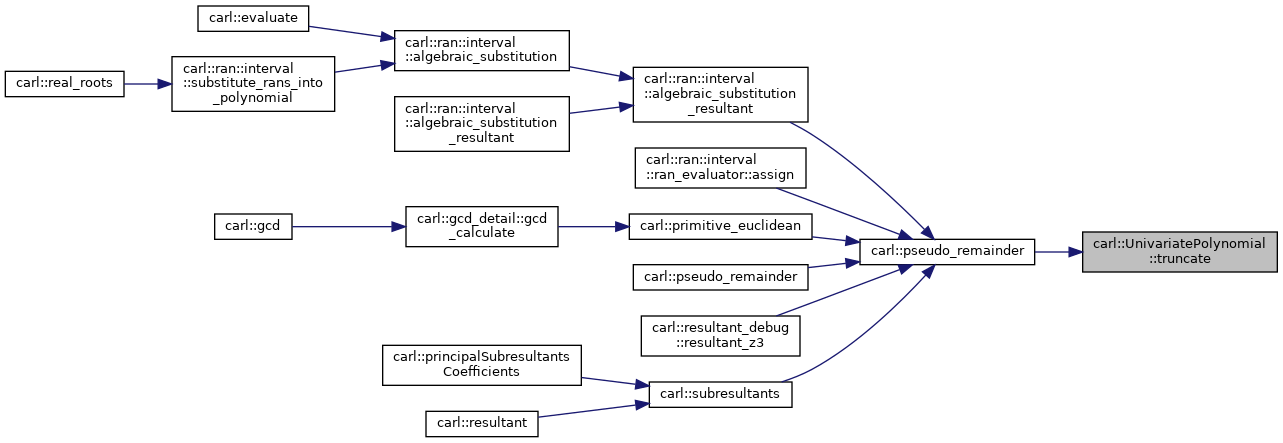
◆ truncate()
|
inline |
Removes the leading term from the polynomial.
Definition at line 315 of file UnivariatePolynomial.h.

◆ unit_part()
| Coefficient carl::UnivariatePolynomial< Coefficient >::unit_part | ( | ) | const |
The unit part of a polynomial over a field is its leading coefficient for nonzero polynomials, and one for zero polynomials.
The unit part of a polynomial over a ring is the sign of the polynomial for nonzero polynomials, and one for zero polynomials.
- See also
- [3], page 42.
- Returns
- The unit part of the polynomial.
◆ zero_is_root()
|
inline |
Checks if zero is a real root of this polynomial.
- Returns
- True if zero is a root.
Definition at line 596 of file UnivariatePolynomial.h.

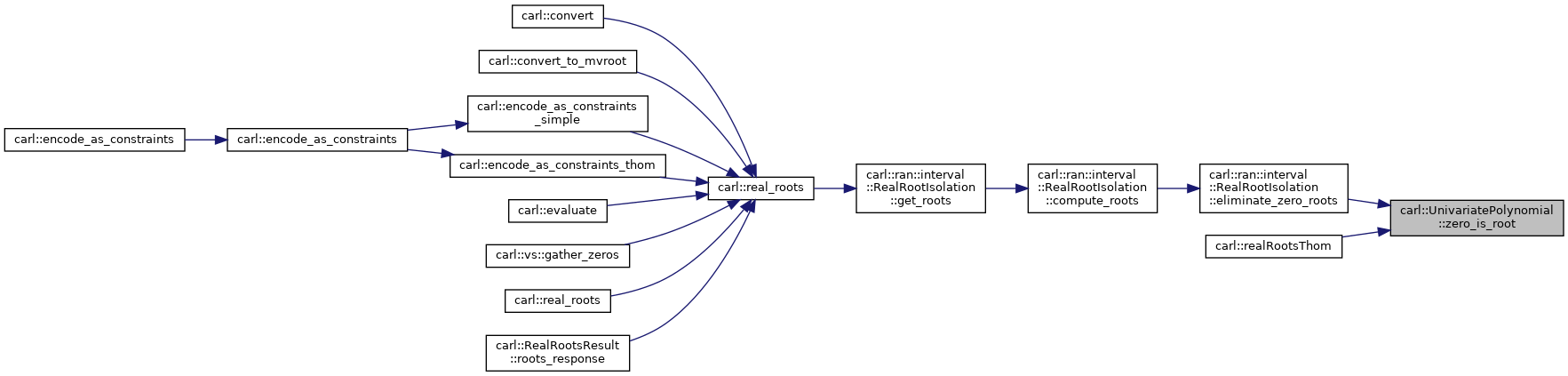
Friends And Related Function Documentation
◆ operator!= [1/2]
|
friend |
Checks if the two arguments are not equal.
- Parameters
-
lhs First argument. rhs Second argument.
- Returns
lhs != rhs
◆ operator!= [2/2]
|
friend |
Checks if the two arguments are not equal.
- Parameters
-
lhs First argument. rhs Second argument.
- Returns
lhs != rhs
◆ operator* [1/9]
|
friend |
Perform a multiplication involving a polynomial.
- Parameters
-
lhs Left hand side. rhs Right hand side.
- Returns
lhs * rhs
◆ operator* [2/9]
|
friend |
Perform a multiplication involving a polynomial.
- Parameters
-
lhs Left hand side. rhs Right hand side.
- Returns
lhs * rhs
◆ operator* [3/9]
|
friend |
Perform a multiplication involving a polynomial.
- Parameters
-
lhs Left hand side. rhs Right hand side.
- Returns
lhs * rhs
◆ operator* [4/9]
|
friend |
Perform a multiplication involving a polynomial.
- Parameters
-
lhs Left hand side. rhs Right hand side.
- Returns
lhs * rhs
◆ operator* [5/9]
|
friend |
Perform a multiplication involving a polynomial.
- Parameters
-
lhs Left hand side. rhs Right hand side.
- Returns
lhs * rhs
◆ operator* [6/9]
|
friend |
Perform a multiplication involving a polynomial.
- Parameters
-
lhs Left hand side. rhs Right hand side.
- Returns
lhs * rhs
◆ operator* [7/9]
|
friend |
Perform a multiplication involving a polynomial.
- Parameters
-
lhs Left hand side. rhs Right hand side.
- Returns
lhs * rhs
◆ operator* [8/9]
|
friend |
Perform a multiplication involving a polynomial.
- Parameters
-
lhs Left hand side. rhs Right hand side.
- Returns
lhs * rhs
◆ operator* [9/9]
|
friend |
Perform a multiplication involving a polynomial.
- Parameters
-
lhs Left hand side. rhs Right hand side.
- Returns
lhs * rhs
◆ operator+ [1/3]
|
friend |
Performs an addition involving a polynomial.
- Parameters
-
lhs First argument. rhs Second argument.
- Returns
lhs + rhs
◆ operator+ [2/3]
|
friend |
Performs an addition involving a polynomial.
- Parameters
-
lhs First argument. rhs Second argument.
- Returns
lhs + rhs
◆ operator+ [3/3]
|
friend |
Performs an addition involving a polynomial.
- Parameters
-
lhs First argument. rhs Second argument.
- Returns
lhs + rhs
◆ operator- [1/3]
|
friend |
Performs a subtraction involving a polynomial.
- Parameters
-
lhs First argument. rhs Second argument.
- Returns
lhs - rhs
◆ operator- [2/3]
|
friend |
Performs a subtraction involving a polynomial.
- Parameters
-
lhs First argument. rhs Second argument.
- Returns
lhs - rhs
◆ operator- [3/3]
|
friend |
Performs a subtraction involving a polynomial.
- Parameters
-
lhs First argument. rhs Second argument.
- Returns
lhs - rhs
◆ operator/
|
friend |
Perform a division involving a polynomial.
- Parameters
-
lhs Left hand side. rhs Right hand side.
- Returns
lhs / rhs
◆ operator<
|
friend |
◆ operator<<
|
friend |
Streaming operator for univariate polynomials.
- Parameters
-
os Output stream. rhs Polynomial.
- Returns
os
◆ operator== [1/4]
|
friend |
Checks if the two arguments are equal.
- Parameters
-
lhs First argument. rhs Second argument.
- Returns
lhs == rhs
◆ operator== [2/4]
|
friend |
Checks if the two arguments are equal.
- Parameters
-
lhs First argument. rhs Second argument.
- Returns
lhs == rhs
◆ operator== [3/4]
|
friend |
Checks if the two arguments are equal.
- Parameters
-
lhs First argument. rhs Second argument.
- Returns
lhs == rhs
◆ operator== [4/4]
|
friend |
Checks if the two arguments are equal.
- Parameters
-
lhs First argument. rhs Second argument.
- Returns
lhs == rhs
◆ UnivariatePolynomial
Declare all instantiations of univariate polynomials as friends.
Definition at line 66 of file UnivariatePolynomial.h.
Field Documentation
◆ mCoefficients
|
private |
The coefficients.
Definition at line 71 of file UnivariatePolynomial.h.
◆ mMainVar
|
private |
The main variable.
Definition at line 69 of file UnivariatePolynomial.h.
The documentation for this class was generated from the following files:
- carl-arith/numbers/typetraits.h
- carl-arith/poly/umvpoly/UnivariatePolynomial.h


