The general-purpose multivariate polynomial class. More...
#include <MultivariatePolynomial.h>

Public Types | |
| enum class | ConstructorOperation { ADD , SUB , MUL , DIV } |
| using | OrderedBy = Ordering |
| The ordering of the terms. More... | |
| using | TermType = Term< Coeff > |
| Type of the terms. More... | |
| using | MonomType = Monomial |
| Type of the monomials within the terms. More... | |
| using | CoeffType = Coeff |
| Type of the coefficients. More... | |
| using | Policy = Policies |
| Policies for this monomial. More... | |
| using | NumberType = typename UnderlyingNumberType< Coeff >::type |
| Number type within the coefficients. More... | |
| using | IntNumberType = typename IntegralType< NumberType >::type |
| Integer type associated with the number type. More... | |
| using | PolyType = MultivariatePolynomial< Coeff, Ordering, Policies > |
| using | CACHE = void |
| The type of the cache. Multivariate polynomials do not need a cache, we set it to something. More... | |
| using | TermsType = std::vector< Term< Coeff > > |
| Type our terms vector.f. More... | |
| using | RootType = typename UnivariatePolynomial< NumberType >::RootType |
| template<typename C , typename T > | |
| using | EnableIfNotSame = typename std::enable_if<!std::is_same< C, T >::value, T >::type |
Public Member Functions | |
| ~MultivariatePolynomial () noexcept=default | |
| bool | isOrdered () const |
| Check if the terms are ordered. More... | |
| void | reset_ordered () const |
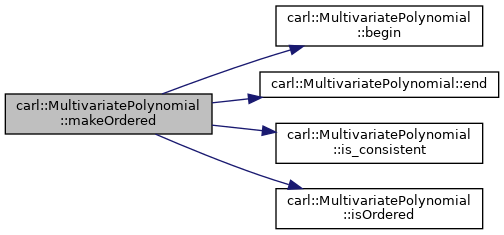
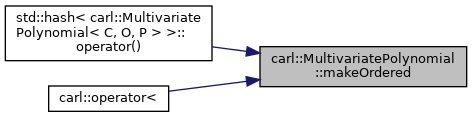
| void | makeOrdered () const |
| Ensure that the terms are ordered. More... | |
| const Term< Coeff > & | lterm () const |
| The leading term. More... | |
| Term< Coeff > & | lterm () |
| const Coeff & | lcoeff () const |
| Returns the coefficient of the leading term. More... | |
| const Monomial::Arg & | lmon () const |
| The leading monomial. More... | |
| MultivariatePolynomial | lcoeff (Variable::Arg var) const |
| Returns the leading coefficient with respect to the given variable. More... | |
| const Term< Coeff > & | trailingTerm () const |
| Give the last term according to Ordering. More... | |
| Term< Coeff > & | trailingTerm () |
| std::size_t | total_degree () const |
| Calculates the max. More... | |
| std::size_t | degree (Variable::Arg var) const |
| Calculates the degree of this polynomial with respect to the given variable. More... | |
| MultivariatePolynomial | coeff (Variable::Arg var, std::size_t exp) const |
| Calculates the coefficient of var^exp. More... | |
| bool | is_zero () const |
| Check if the polynomial is zero. More... | |
| bool | is_one () const |
| bool | is_constant () const |
| Check if the polynomial is constant. More... | |
| bool | is_number () const |
| Check if the polynomial is a number, i.e., a constant. More... | |
| bool | is_variable () const |
| bool | is_linear () const |
| Check if the polynomial is linear. More... | |
| std::size_t | nr_terms () const |
| Calculate the number of terms. More... | |
| std::size_t | size () const |
| bool | has_constant_term () const |
| Check if the polynomial has a constant term that is not zero. More... | |
| bool | integer_valued () const |
| const Coeff & | constant_part () const |
| Retrieve the constant term of this polynomial or zero, if there is no constant term. More... | |
| auto | begin () const |
| auto | end () const |
| auto | rbegin () const |
| auto | rend () const |
| auto | erase_term (typename TermsType::iterator pos) |
| const TermsType & | terms () const |
| TermsType & | terms () |
| MultivariatePolynomial | tail (bool makeFullyOrdered=false) const |
| For the polynomial p, the function calculates a polynomial p - lt(p). More... | |
| MultivariatePolynomial & | strip_lterm () |
| Drops the leading term. More... | |
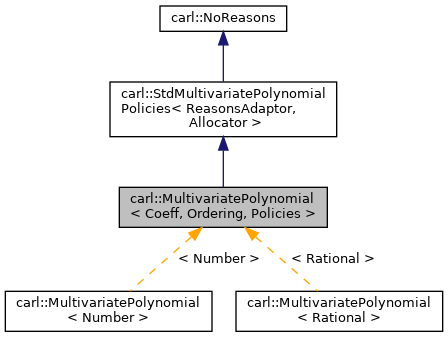
| bool | has_single_variable () const |
| Variable | single_variable () const |
| For terms with exactly one variable, get this variable. More... | |
| const CoeffType & | coefficient () const |
| const PolyType & | polynomial () const |
| bool | is_univariate () const |
| Checks whether only one variable occurs. More... | |
| bool | is_tsos () const |
| Checks whether the polynomial is a trivial sum of squares. More... | |
| bool | has (Variable v) const |
| bool | is_reducible_identity () const |
| void | subtractProduct (const Term< Coeff > &factor, const MultivariatePolynomial &p) |
| Subtract a term times a polynomial from this polynomial. More... | |
| void | addTerm (const Term< Coeff > &term) |
| Adds a single term without using a TermAdditionManager or changing the ordering status. More... | |
| bool | sqrt (MultivariatePolynomial &res) const |
| Calculates the square of this multivariate polynomial if it is a square. More... | |
| Coeff | coprime_factor () const |
| template<typename C = Coeff, EnableIf< is_subset_of_rationals_type< C >> = dummy> | |
| Coeff | coprime_factor_without_constant () const |
| MultivariatePolynomial | coprime_coefficients () const |
| MultivariatePolynomial | coprime_coefficients_sign_preserving () const |
| MultivariatePolynomial | normalize () const |
| For a polynomial p, returns p/lc(p) More... | |
| bool | divides (const MultivariatePolynomial &b) const |
| MultivariatePolynomial< typename IntegralType< Coeff >::type, Ordering, Policies > | to_integer_domain () const |
| const Term< Coeff > & | operator[] (std::size_t index) const |
| MultivariatePolynomial | mod (const typename IntegralType< Coeff >::type &modulo) const |
| template<typename C = Coeff, EnableIf< is_number_type< C >> = dummy> | |
| Coeff | numeric_content () const |
| template<typename C = Coeff, DisableIf< is_number_type< C >> = dummy> | |
| UnderlyingNumberType< C >::type | numeric_content () const |
| template<typename C = Coeff, EnableIf< is_number_type< C >> = dummy> | |
| IntNumberType | main_denom () const |
| MultivariatePolynomial | operator- () const |
| template<bool findConstantTerm = true, bool findLeadingTerm = true> | |
| void | makeMinimallyOrdered () const |
| Make sure that the terms are at least minimally ordered. More... | |
| bool | is_consistent () const |
| Asserts that this polynomial complies with the requirements and assumptions for MultivariatePolynomial objects. More... | |
| void | setReason (unsigned index) |
| BitVector | getReasons () const |
| void | setReasons (const BitVector &) const |
Constructors | |
| MultivariatePolynomial () | |
| MultivariatePolynomial (const MultivariatePolynomial< Coeff, Ordering, Policies > &p) | |
| MultivariatePolynomial (MultivariatePolynomial< Coeff, Ordering, Policies > &&p) | |
| MultivariatePolynomial & | operator= (const MultivariatePolynomial &p) |
| MultivariatePolynomial & | operator= (MultivariatePolynomial &&p) noexcept |
| MultivariatePolynomial (int c) | |
| template<typename C = Coeff> | |
| MultivariatePolynomial (EnableIfNotSame< C, sint > c) | |
| template<typename C = Coeff> | |
| MultivariatePolynomial (EnableIfNotSame< C, uint > c) | |
| MultivariatePolynomial (const Coeff &c) | |
| MultivariatePolynomial (Variable::Arg v) | |
| MultivariatePolynomial (const Term< Coeff > &t) | |
| MultivariatePolynomial (const std::shared_ptr< const Monomial > &m) | |
| MultivariatePolynomial (const UnivariatePolynomial< MultivariatePolynomial< Coeff, Ordering, Policy >> &pol) | |
| MultivariatePolynomial (const UnivariatePolynomial< Coeff > &p) | |
| template<class OtherPolicies , DisableIf< std::is_same< Policies, OtherPolicies >> = dummy> | |
| MultivariatePolynomial (const MultivariatePolynomial< Coeff, Ordering, OtherPolicies > &p) | |
| MultivariatePolynomial (TermsType &&terms, bool duplicates=true, bool ordered=false) | |
| MultivariatePolynomial (const TermsType &terms, bool duplicates=true, bool ordered=false) | |
| MultivariatePolynomial (const std::initializer_list< Term< Coeff >> &terms) | |
| MultivariatePolynomial (const std::initializer_list< Variable > &terms) | |
| MultivariatePolynomial (const std::pair< ConstructorOperation, std::vector< MultivariatePolynomial >> &p) | |
| MultivariatePolynomial (ConstructorOperation op, const std::vector< MultivariatePolynomial > &operands) | |
In-place addition operators | |
| MultivariatePolynomial & | operator+= (const MultivariatePolynomial &rhs) |
| Add something to this polynomial and return the changed polynomial. More... | |
| MultivariatePolynomial & | operator+= (const TermType &rhs) |
| Add something to this polynomial and return the changed polynomial. More... | |
| MultivariatePolynomial & | operator+= (const std::shared_ptr< const TermType > &rhs) |
| Add something to this polynomial and return the changed polynomial. More... | |
| MultivariatePolynomial & | operator+= (const Monomial::Arg &rhs) |
| Add something to this polynomial and return the changed polynomial. More... | |
| MultivariatePolynomial & | operator+= (Variable rhs) |
| Add something to this polynomial and return the changed polynomial. More... | |
| MultivariatePolynomial & | operator+= (const Coeff &rhs) |
| Add something to this polynomial and return the changed polynomial. More... | |
In-place subtraction operators | |
| MultivariatePolynomial & | operator-= (const MultivariatePolynomial &rhs) |
| Subtract something from this polynomial and return the changed polynomial. More... | |
| MultivariatePolynomial & | operator-= (const Term< Coeff > &rhs) |
| Subtract something from this polynomial and return the changed polynomial. More... | |
| MultivariatePolynomial & | operator-= (const Monomial::Arg &rhs) |
| Subtract something from this polynomial and return the changed polynomial. More... | |
| MultivariatePolynomial & | operator-= (Variable::Arg rhs) |
| Subtract something from this polynomial and return the changed polynomial. More... | |
| MultivariatePolynomial & | operator-= (const Coeff &rhs) |
| Subtract something from this polynomial and return the changed polynomial. More... | |
In-place multiplication operators | |
| MultivariatePolynomial & | operator*= (const MultivariatePolynomial &rhs) |
| Multiply this polynomial with something and return the changed polynomial. More... | |
| MultivariatePolynomial & | operator*= (const Term< Coeff > &rhs) |
| Multiply this polynomial with something and return the changed polynomial. More... | |
| MultivariatePolynomial & | operator*= (const Monomial::Arg &rhs) |
| Multiply this polynomial with something and return the changed polynomial. More... | |
| MultivariatePolynomial & | operator*= (Variable::Arg rhs) |
| Multiply this polynomial with something and return the changed polynomial. More... | |
| MultivariatePolynomial & | operator*= (const Coeff &rhs) |
| Multiply this polynomial with something and return the changed polynomial. More... | |
In-place division operators | |
| MultivariatePolynomial & | operator/= (const MultivariatePolynomial &rhs) |
| Divide this polynomial by something and return the changed polynomial. More... | |
| MultivariatePolynomial & | operator/= (const Term< Coeff > &rhs) |
| Divide this polynomial by something and return the changed polynomial. More... | |
| MultivariatePolynomial & | operator/= (const Monomial::Arg &rhs) |
| Divide this polynomial by something and return the changed polynomial. More... | |
| MultivariatePolynomial & | operator/= (Variable::Arg rhs) |
| Divide this polynomial by something and return the changed polynomial. More... | |
| MultivariatePolynomial & | operator/= (const Coeff &rhs) |
| Divide this polynomial by something and return the changed polynomial. More... | |
Static Public Member Functions | |
| static bool | compareByLeadingTerm (const MultivariatePolynomial &p1, const MultivariatePolynomial &p2) |
| static bool | compareByNrTerms (const MultivariatePolynomial &p1, const MultivariatePolynomial &p2) |
Static Public Attributes | |
| static TermAdditionManager< MultivariatePolynomial, Ordering > | mTermAdditionManager |
| static const bool | searchLinear = true |
| Linear searching means that we search linearly for a term instead of applying e.g. More... | |
| static const bool | has_reasons = ReasonsAdaptor::has_reasons |
Private Member Functions | |
| void | makeMinimallyOrdered (typename TermsType::iterator <erm, typename TermsType::iterator &cterm) const |
| Make sure that the terms are at least minimally ordered. More... | |
Private Attributes | |
| TermsType | mTerms |
| A vector of all terms. More... | |
| bool | mOrdered |
| Flag that indicates if the terms are ordered. More... | |
Friends | |
| template<typename Polynomial , typename Order > | |
| class | TermAdditionManager |
| std::ostream & | operator<< (std::ostream &os, ConstructorOperation op) |
Division operators | |
| template<typename C , typename O , typename P > | |
| MultivariatePolynomial< C, O, P > | operator/ (const MultivariatePolynomial< C, O, P > &lhs, const MultivariatePolynomial< C, O, P > &rhs) |
| Perform a division involving a polynomial. More... | |
| template<typename C , typename O , typename P > | |
| MultivariatePolynomial< C, O, P > | operator/ (const MultivariatePolynomial< C, O, P > &lhs, unsigned long rhs) |
| Perform a division involving a polynomial. More... | |
Detailed Description
template<typename Coeff, typename Ordering = GrLexOrdering, typename Policies = StdMultivariatePolynomialPolicies<>>
class carl::MultivariatePolynomial< Coeff, Ordering, Policies >
The general-purpose multivariate polynomial class.
It is represented as a sum of terms, being a coefficient and a monomial.
A polynomial is always minimally ordered. By that, we mean that the leading term and the constant term (if there is any) are at the correct positions. For some operations, the terms may be fully ordered. isOrdered() checks if the polynomial is fully ordered while makeOrdered() makes the polynomial fully ordered.
Definition at line 42 of file MultivariatePolynomial.h.
Member Typedef Documentation
◆ CACHE
| using carl::MultivariatePolynomial< Coeff, Ordering, Policies >::CACHE = void |
The type of the cache. Multivariate polynomials do not need a cache, we set it to something.
Definition at line 64 of file MultivariatePolynomial.h.
◆ CoeffType
| using carl::MultivariatePolynomial< Coeff, Ordering, Policies >::CoeffType = Coeff |
Type of the coefficients.
Definition at line 54 of file MultivariatePolynomial.h.
◆ EnableIfNotSame
| using carl::MultivariatePolynomial< Coeff, Ordering, Policies >::EnableIfNotSame = typename std::enable_if<!std::is_same<C,T>::value,T>::type |
Definition at line 71 of file MultivariatePolynomial.h.
◆ IntNumberType
| using carl::MultivariatePolynomial< Coeff, Ordering, Policies >::IntNumberType = typename IntegralType<NumberType>::type |
Integer type associated with the number type.
Definition at line 60 of file MultivariatePolynomial.h.
◆ MonomType
| using carl::MultivariatePolynomial< Coeff, Ordering, Policies >::MonomType = Monomial |
Type of the monomials within the terms.
Definition at line 52 of file MultivariatePolynomial.h.
◆ NumberType
| using carl::MultivariatePolynomial< Coeff, Ordering, Policies >::NumberType = typename UnderlyingNumberType<Coeff>::type |
Number type within the coefficients.
Definition at line 58 of file MultivariatePolynomial.h.
◆ OrderedBy
| using carl::MultivariatePolynomial< Coeff, Ordering, Policies >::OrderedBy = Ordering |
The ordering of the terms.
Definition at line 48 of file MultivariatePolynomial.h.
◆ Policy
| using carl::MultivariatePolynomial< Coeff, Ordering, Policies >::Policy = Policies |
Policies for this monomial.
Definition at line 56 of file MultivariatePolynomial.h.
◆ PolyType
| using carl::MultivariatePolynomial< Coeff, Ordering, Policies >::PolyType = MultivariatePolynomial<Coeff, Ordering, Policies> |
Definition at line 62 of file MultivariatePolynomial.h.
◆ RootType
| using carl::MultivariatePolynomial< Coeff, Ordering, Policies >::RootType = typename UnivariatePolynomial<NumberType>::RootType |
Definition at line 68 of file MultivariatePolynomial.h.
◆ TermsType
| using carl::MultivariatePolynomial< Coeff, Ordering, Policies >::TermsType = std::vector<Term<Coeff> > |
Type our terms vector.f.
Definition at line 66 of file MultivariatePolynomial.h.
◆ TermType
| using carl::MultivariatePolynomial< Coeff, Ordering, Policies >::TermType = Term<Coeff> |
Type of the terms.
Definition at line 50 of file MultivariatePolynomial.h.
Member Enumeration Documentation
◆ ConstructorOperation
|
strong |
| Enumerator | |
|---|---|
| ADD | |
| SUB | |
| MUL | |
| DIV | |
Definition at line 82 of file MultivariatePolynomial.h.
Constructor & Destructor Documentation
◆ MultivariatePolynomial() [1/19]
| carl::MultivariatePolynomial< Coeff, Ordering, Policies >::MultivariatePolynomial | ( | ) |
◆ MultivariatePolynomial() [2/19]
| carl::MultivariatePolynomial< Coeff, Ordering, Policies >::MultivariatePolynomial | ( | const MultivariatePolynomial< Coeff, Ordering, Policies > & | p | ) |
◆ MultivariatePolynomial() [3/19]
| carl::MultivariatePolynomial< Coeff, Ordering, Policies >::MultivariatePolynomial | ( | MultivariatePolynomial< Coeff, Ordering, Policies > && | p | ) |
◆ MultivariatePolynomial() [4/19]
|
inlineexplicit |
Definition at line 100 of file MultivariatePolynomial.h.
◆ MultivariatePolynomial() [5/19]
|
explicit |
◆ MultivariatePolynomial() [6/19]
|
explicit |
◆ MultivariatePolynomial() [7/19]
|
explicit |
◆ MultivariatePolynomial() [8/19]
|
explicit |
◆ MultivariatePolynomial() [9/19]
|
explicit |
◆ MultivariatePolynomial() [10/19]
|
explicit |
◆ MultivariatePolynomial() [11/19]
|
explicit |
◆ MultivariatePolynomial() [12/19]
|
explicit |
◆ MultivariatePolynomial() [13/19]
|
explicit |
◆ MultivariatePolynomial() [14/19]
|
explicit |
◆ MultivariatePolynomial() [15/19]
|
explicit |
◆ MultivariatePolynomial() [16/19]
| carl::MultivariatePolynomial< Coeff, Ordering, Policies >::MultivariatePolynomial | ( | const std::initializer_list< Term< Coeff >> & | terms | ) |
◆ MultivariatePolynomial() [17/19]
| carl::MultivariatePolynomial< Coeff, Ordering, Policies >::MultivariatePolynomial | ( | const std::initializer_list< Variable > & | terms | ) |
◆ MultivariatePolynomial() [18/19]
|
explicit |
◆ MultivariatePolynomial() [19/19]
|
explicit |
◆ ~MultivariatePolynomial()
|
defaultnoexcept |
Member Function Documentation
◆ addTerm()
| void carl::MultivariatePolynomial< Coeff, Ordering, Policies >::addTerm | ( | const Term< Coeff > & | term | ) |
Adds a single term without using a TermAdditionManager or changing the ordering status.
- Parameters
-
term Term.
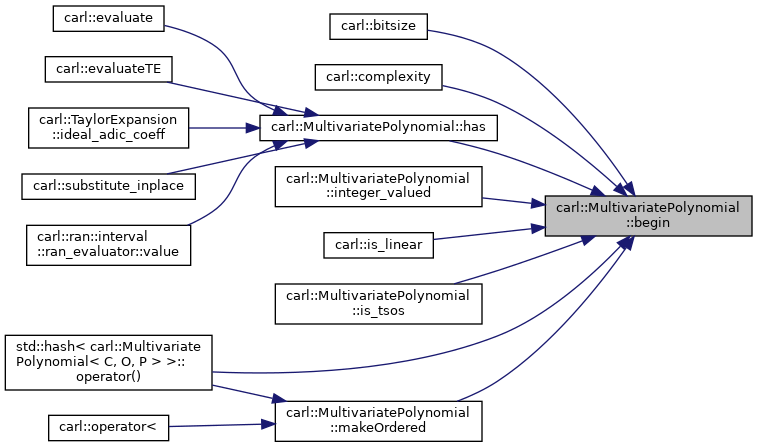
◆ begin()
|
inline |
Definition at line 310 of file MultivariatePolynomial.h.
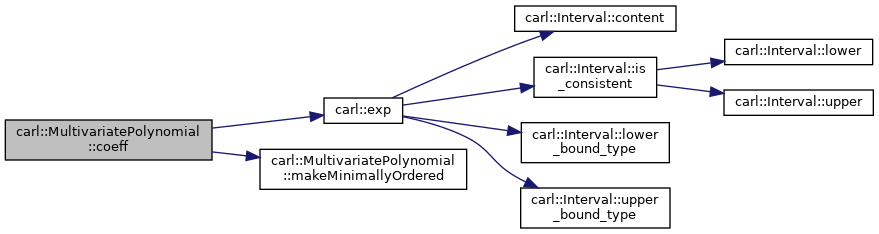
◆ coeff()
|
inline |
Calculates the coefficient of var^exp.
- Parameters
-
var Variable. exp Exponent.
- Returns
- Coefficient of var^exp.
Definition at line 221 of file MultivariatePolynomial.h.

◆ coefficient()
|
inline |
- Returns
- Coefficient of the polynomial (this makes only sense for polynomials storing the gcd of all coefficients separately)
Definition at line 365 of file MultivariatePolynomial.h.

◆ compareByLeadingTerm()
|
inlinestatic |
◆ compareByNrTerms()
|
inlinestatic |
◆ constant_part()
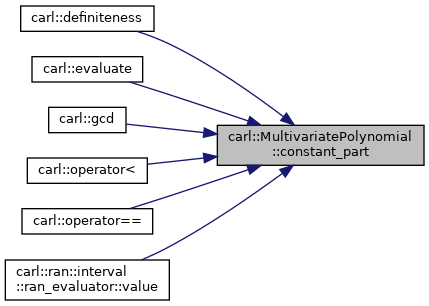
| const Coeff& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::constant_part | ( | ) | const |
Retrieve the constant term of this polynomial or zero, if there is no constant term.
◆ coprime_coefficients()
| MultivariatePolynomial carl::MultivariatePolynomial< Coeff, Ordering, Policies >::coprime_coefficients | ( | ) | const |
- Returns
- p * p.coprime_factor()
- See also
- coprime_factor()
◆ coprime_coefficients_sign_preserving()
| MultivariatePolynomial carl::MultivariatePolynomial< Coeff, Ordering, Policies >::coprime_coefficients_sign_preserving | ( | ) | const |
- Returns
- p * |p.coprime_factor()|
- See also
- coprime_coefficients()
◆ coprime_factor()
| Coeff carl::MultivariatePolynomial< Coeff, Ordering, Policies >::coprime_factor | ( | ) | const |
- Returns
- The lcm of the denominators of the coefficients in p divided by the gcd of numerators of the coefficients in p.
◆ coprime_factor_without_constant()
| Coeff carl::MultivariatePolynomial< Coeff, Ordering, Policies >::coprime_factor_without_constant | ( | ) | const |
- Returns
- The lcm of the denominators of the coefficients (without the constant one) in p divided by the gcd of numerators of the coefficients in p.
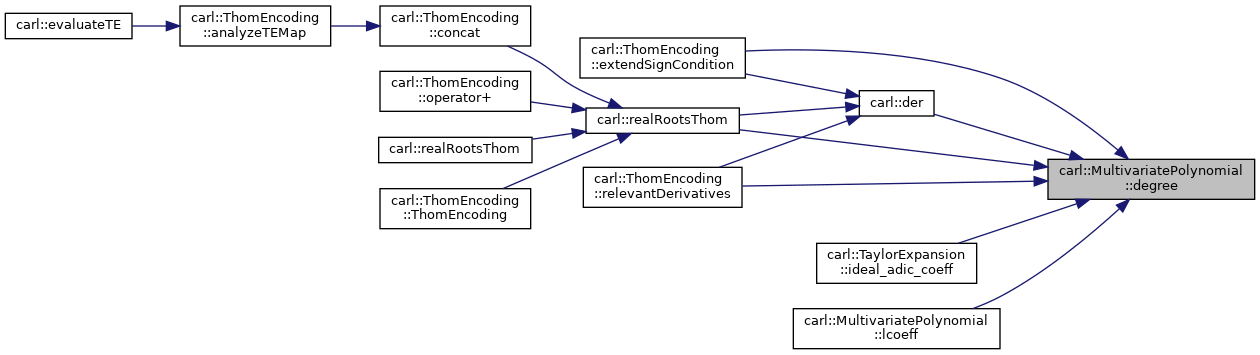
◆ degree()
|
inline |
Calculates the degree of this polynomial with respect to the given variable.
- Parameters
-
var Variable.
- Returns
- Degree w.r.t. var.
Definition at line 205 of file MultivariatePolynomial.h.
◆ divides()
| bool carl::MultivariatePolynomial< Coeff, Ordering, Policies >::divides | ( | const MultivariatePolynomial< Coeff, Ordering, Policies > & | b | ) | const |

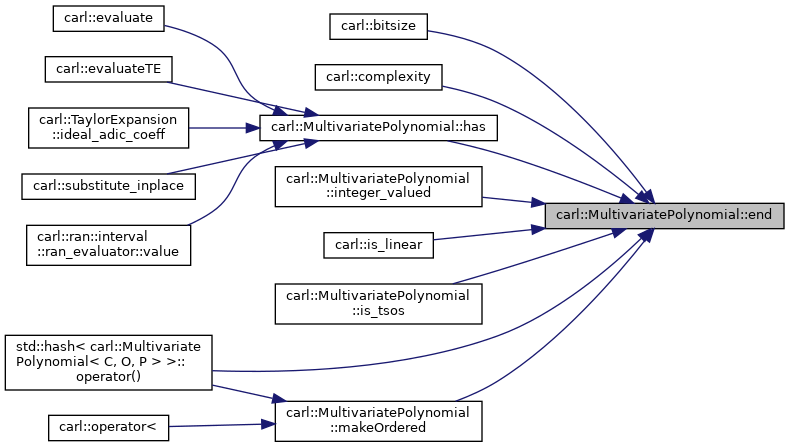
◆ end()
|
inline |
Definition at line 313 of file MultivariatePolynomial.h.
◆ erase_term()
|
inline |
- Todo:
- find new lterm or constant term
Definition at line 323 of file MultivariatePolynomial.h.
◆ getReasons()
|
inlineinherited |
Definition at line 17 of file ReasonsAdaptor.h.
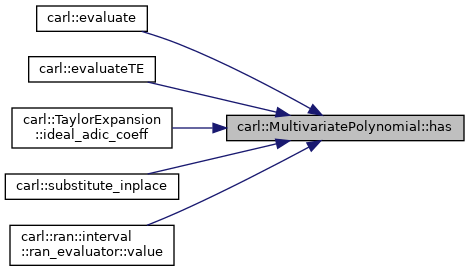
◆ has()
|
inline |
- Parameters
-
v The variable to check for its occurrence.
- Returns
- true, if the variable occurs in this term.
Definition at line 397 of file MultivariatePolynomial.h.

◆ has_constant_term()
|
inline |
Check if the polynomial has a constant term that is not zero.
Definition at line 292 of file MultivariatePolynomial.h.


◆ has_single_variable()
|
inline |
◆ integer_valued()
|
inline |
- Returns
- true, if the image of this polynomial is integer-valued.
Definition at line 299 of file MultivariatePolynomial.h.
◆ is_consistent()
| bool carl::MultivariatePolynomial< Coeff, Ordering, Policies >::is_consistent | ( | ) | const |
Asserts that this polynomial complies with the requirements and assumptions for MultivariatePolynomial objects.
- All terms are actually valid and not nullptr or alike
- Only the trailing term may be constant.
◆ is_constant()
|
inline |
Check if the polynomial is constant.
Definition at line 254 of file MultivariatePolynomial.h.


◆ is_linear()
| bool carl::MultivariatePolynomial< Coeff, Ordering, Policies >::is_linear | ( | ) | const |
Check if the polynomial is linear.

◆ is_number()
|
inline |
Check if the polynomial is a number, i.e., a constant.
Definition at line 260 of file MultivariatePolynomial.h.


◆ is_one()
|
inline |
- Returns
Definition at line 248 of file MultivariatePolynomial.h.

◆ is_reducible_identity()
| bool carl::MultivariatePolynomial< Coeff, Ordering, Policies >::is_reducible_identity | ( | ) | const |
◆ is_tsos()
|
inline |
Checks whether the polynomial is a trivial sum of squares.
- Returns
- true if polynomial is of the form \sum a_im_i^2 with a_i > 0 for all i.
Definition at line 387 of file MultivariatePolynomial.h.
◆ is_univariate()
| bool carl::MultivariatePolynomial< Coeff, Ordering, Policies >::is_univariate | ( | ) | const |
Checks whether only one variable occurs.
- Returns
- Notice that it might be better to use the variable information if several pieces of information are requested.
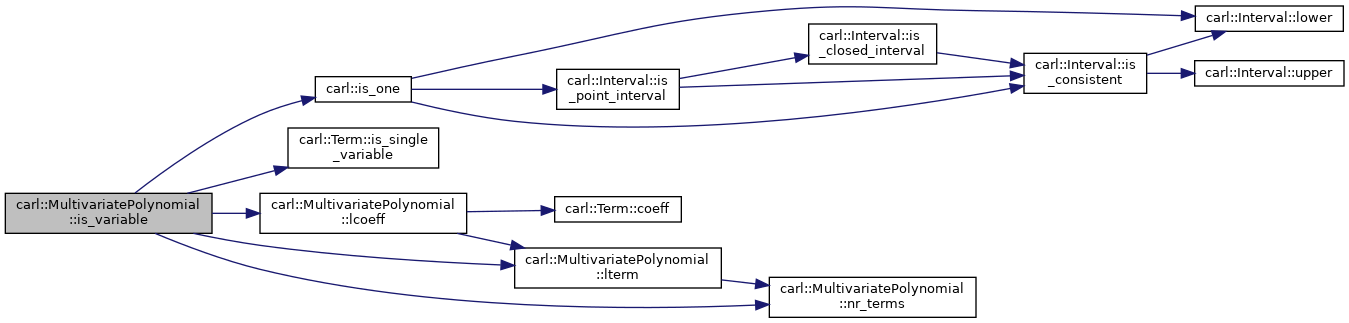
◆ is_variable()
|
inline |
- Returns
- true, if this polynomial consists just of one variable (with coefficient 1).
Definition at line 266 of file MultivariatePolynomial.h.
◆ is_zero()
|
inline |
Check if the polynomial is zero.
Definition at line 240 of file MultivariatePolynomial.h.
◆ isOrdered()
|
inline |
Check if the terms are ordered.
- Returns
- If terms are ordered.
Definition at line 127 of file MultivariatePolynomial.h.

◆ lcoeff() [1/2]
|
inline |
Returns the coefficient of the leading term.
Notice that this is not defined for zero polynomials.
- Returns
- Leading coefficient.
Definition at line 161 of file MultivariatePolynomial.h.


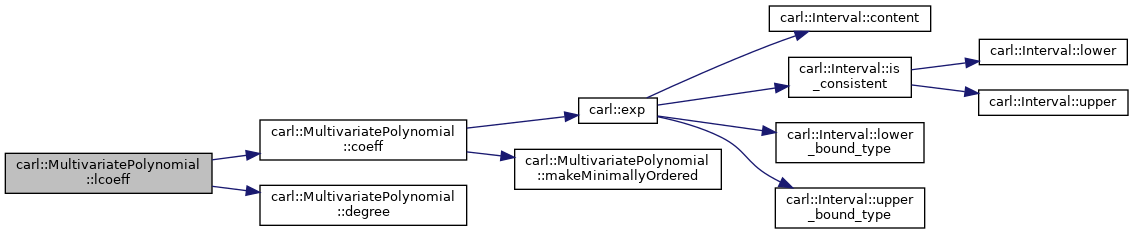
◆ lcoeff() [2/2]
|
inline |
Returns the leading coefficient with respect to the given variable.
- Parameters
-
var Variable.
- Returns
- Leading coefficient.
Definition at line 176 of file MultivariatePolynomial.h.
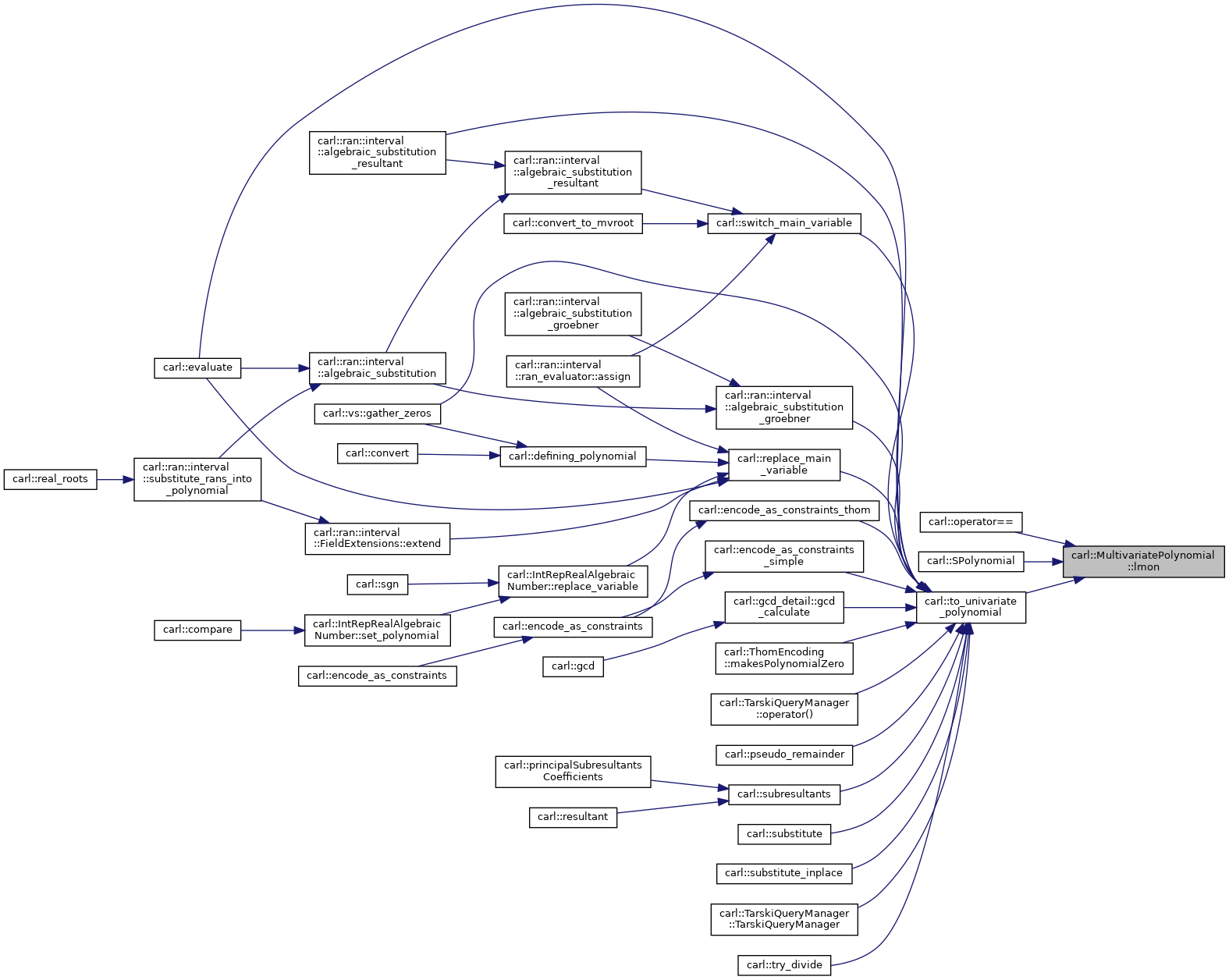
◆ lmon()
|
inline |
The leading monomial.
- Returns
- monomial of leading term.
Definition at line 168 of file MultivariatePolynomial.h.

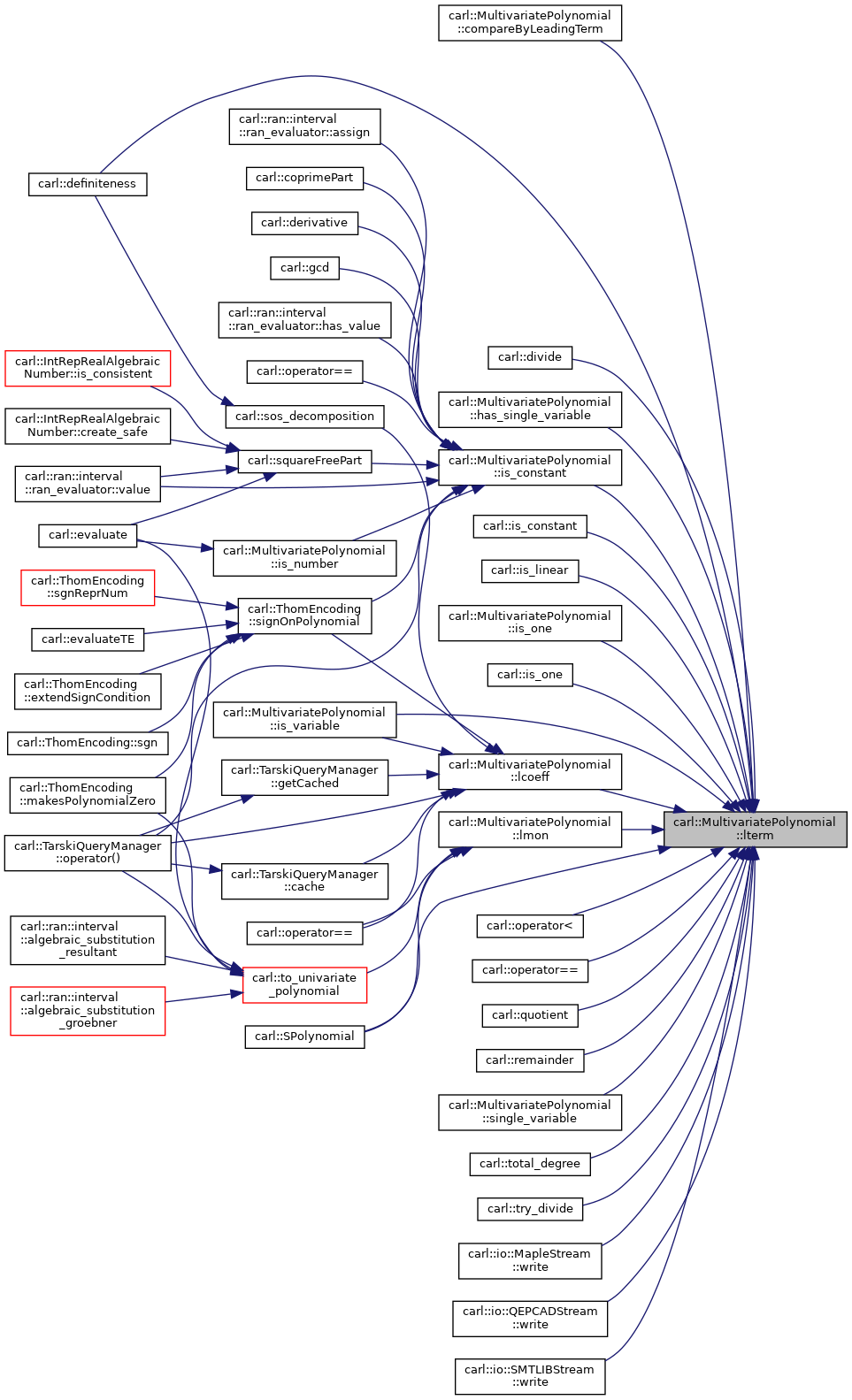
◆ lterm() [1/2]
|
inline |
◆ lterm() [2/2]
|
inline |
The leading term.
- Returns
- leading term.
Definition at line 148 of file MultivariatePolynomial.h.

◆ main_denom()
| IntNumberType carl::MultivariatePolynomial< Coeff, Ordering, Policies >::main_denom | ( | ) | const |
◆ makeMinimallyOrdered() [1/2]
| void carl::MultivariatePolynomial< Coeff, Ordering, Policies >::makeMinimallyOrdered | ( | ) | const |
Make sure that the terms are at least minimally ordered.

◆ makeMinimallyOrdered() [2/2]
|
private |
Make sure that the terms are at least minimally ordered.
Iterators to the important terms are given as arguments, so that we don't need to scan the whole vector.
- Parameters
-
lterm Iterator to leading term. cterm Iterator to constant term.
◆ makeOrdered()
|
inline |
Ensure that the terms are ordered.
Definition at line 136 of file MultivariatePolynomial.h.
◆ mod()
| MultivariatePolynomial carl::MultivariatePolynomial< Coeff, Ordering, Policies >::mod | ( | const typename IntegralType< Coeff >::type & | modulo | ) | const |
◆ normalize()
| MultivariatePolynomial carl::MultivariatePolynomial< Coeff, Ordering, Policies >::normalize | ( | ) | const |
For a polynomial p, returns p/lc(p)
- Returns

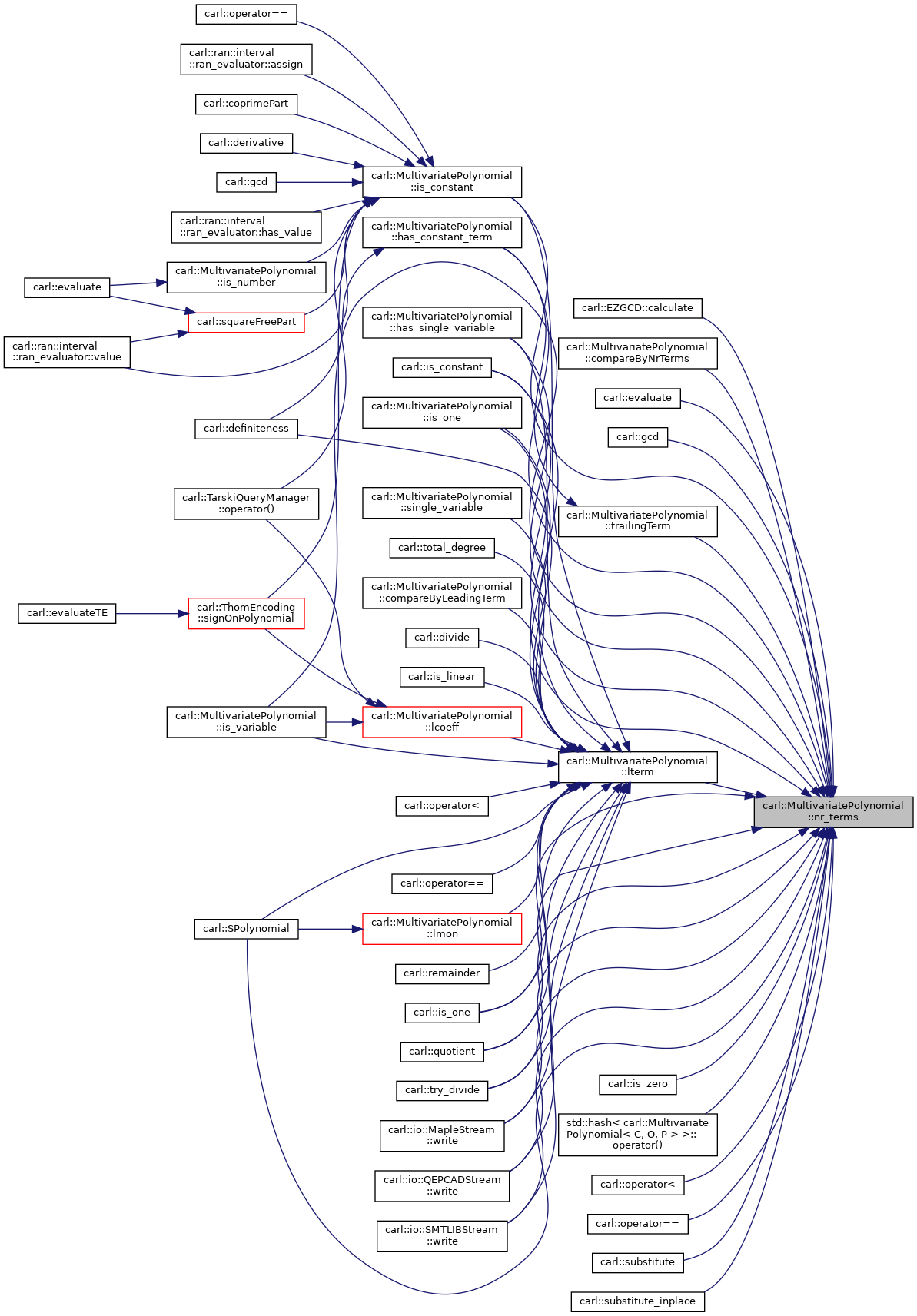
◆ nr_terms()
|
inline |
Calculate the number of terms.
Definition at line 277 of file MultivariatePolynomial.h.
◆ numeric_content() [1/2]
| Coeff carl::MultivariatePolynomial< Coeff, Ordering, Policies >::numeric_content | ( | ) | const |
◆ numeric_content() [2/2]
| UnderlyingNumberType<C>::type carl::MultivariatePolynomial< Coeff, Ordering, Policies >::numeric_content | ( | ) | const |
◆ operator*=() [1/5]
| MultivariatePolynomial& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::operator*= | ( | const Coeff & | rhs | ) |
Multiply this polynomial with something and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator*=() [2/5]
| MultivariatePolynomial& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::operator*= | ( | const Monomial::Arg & | rhs | ) |
Multiply this polynomial with something and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator*=() [3/5]
| MultivariatePolynomial& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::operator*= | ( | const MultivariatePolynomial< Coeff, Ordering, Policies > & | rhs | ) |
Multiply this polynomial with something and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator*=() [4/5]
| MultivariatePolynomial& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::operator*= | ( | const Term< Coeff > & | rhs | ) |
Multiply this polynomial with something and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator*=() [5/5]
| MultivariatePolynomial& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::operator*= | ( | Variable::Arg | rhs | ) |
Multiply this polynomial with something and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator+=() [1/6]
| MultivariatePolynomial& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::operator+= | ( | const Coeff & | rhs | ) |
Add something to this polynomial and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator+=() [2/6]
| MultivariatePolynomial& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::operator+= | ( | const Monomial::Arg & | rhs | ) |
Add something to this polynomial and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator+=() [3/6]
| MultivariatePolynomial& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::operator+= | ( | const MultivariatePolynomial< Coeff, Ordering, Policies > & | rhs | ) |
Add something to this polynomial and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator+=() [4/6]
| MultivariatePolynomial& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::operator+= | ( | const std::shared_ptr< const TermType > & | rhs | ) |
Add something to this polynomial and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator+=() [5/6]
| MultivariatePolynomial& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::operator+= | ( | const TermType & | rhs | ) |
Add something to this polynomial and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator+=() [6/6]
| MultivariatePolynomial& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::operator+= | ( | Variable | rhs | ) |
Add something to this polynomial and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator-()
| MultivariatePolynomial carl::MultivariatePolynomial< Coeff, Ordering, Policies >::operator- | ( | ) | const |
◆ operator-=() [1/5]
| MultivariatePolynomial& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::operator-= | ( | const Coeff & | rhs | ) |
Subtract something from this polynomial and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator-=() [2/5]
| MultivariatePolynomial& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::operator-= | ( | const Monomial::Arg & | rhs | ) |
Subtract something from this polynomial and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator-=() [3/5]
| MultivariatePolynomial& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::operator-= | ( | const MultivariatePolynomial< Coeff, Ordering, Policies > & | rhs | ) |
Subtract something from this polynomial and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator-=() [4/5]
| MultivariatePolynomial& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::operator-= | ( | const Term< Coeff > & | rhs | ) |
Subtract something from this polynomial and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator-=() [5/5]
| MultivariatePolynomial& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::operator-= | ( | Variable::Arg | rhs | ) |
Subtract something from this polynomial and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator/=() [1/5]
| MultivariatePolynomial& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::operator/= | ( | const Coeff & | rhs | ) |
Divide this polynomial by something and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator/=() [2/5]
| MultivariatePolynomial& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::operator/= | ( | const Monomial::Arg & | rhs | ) |
Divide this polynomial by something and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator/=() [3/5]
| MultivariatePolynomial& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::operator/= | ( | const MultivariatePolynomial< Coeff, Ordering, Policies > & | rhs | ) |
Divide this polynomial by something and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator/=() [4/5]
| MultivariatePolynomial& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::operator/= | ( | const Term< Coeff > & | rhs | ) |
Divide this polynomial by something and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator/=() [5/5]
| MultivariatePolynomial& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::operator/= | ( | Variable::Arg | rhs | ) |
Divide this polynomial by something and return the changed polynomial.
- Parameters
-
rhs Right hand side.
- Returns
- Changed polynomial.
◆ operator=() [1/2]
| MultivariatePolynomial& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::operator= | ( | const MultivariatePolynomial< Coeff, Ordering, Policies > & | p | ) |
◆ operator=() [2/2]
|
noexcept |
◆ operator[]()
|
inline |
Definition at line 460 of file MultivariatePolynomial.h.
◆ polynomial()
|
inline |
- Returns
- The coprimeCoefficients of this polyomial, if this is stored internally, otherwise this polynomial.
Definition at line 372 of file MultivariatePolynomial.h.
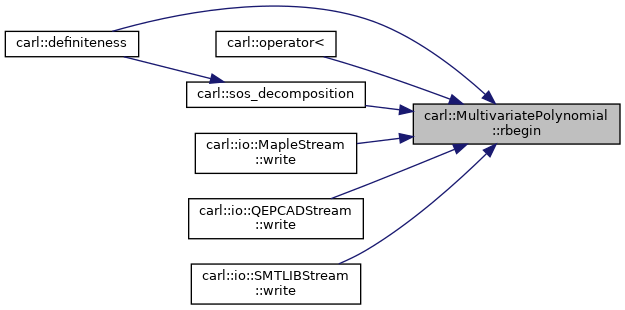
◆ rbegin()
|
inline |
Definition at line 316 of file MultivariatePolynomial.h.
◆ rend()
|
inline |
Definition at line 319 of file MultivariatePolynomial.h.
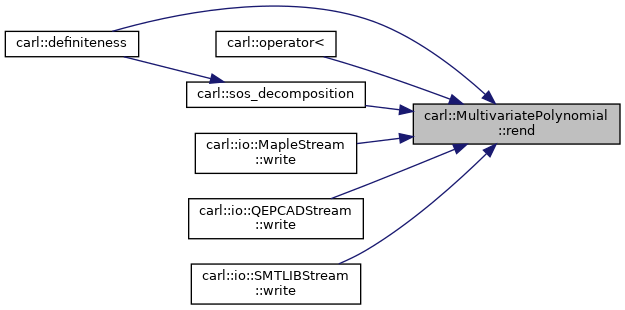
◆ reset_ordered()
|
inline |
Definition at line 130 of file MultivariatePolynomial.h.
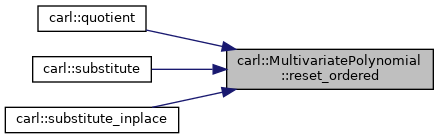
◆ setReason()
|
inherited |
◆ setReasons()
|
inlineinherited |
Definition at line 18 of file ReasonsAdaptor.h.
◆ single_variable()
|
inline |
For terms with exactly one variable, get this variable.
- Returns
- The only variable occuring in the term.
Definition at line 358 of file MultivariatePolynomial.h.

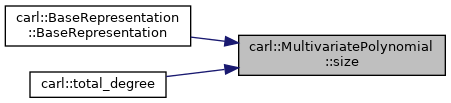
◆ size()
|
inline |
- Returns
- A rough estimation of the size of this polynomial being the number of its terms. (Note, that this method is required, as it is provided of other polynomials not necessarily being straightforward.)
Definition at line 285 of file MultivariatePolynomial.h.
◆ sqrt()
| bool carl::MultivariatePolynomial< Coeff, Ordering, Policies >::sqrt | ( | MultivariatePolynomial< Coeff, Ordering, Policies > & | res | ) | const |
Calculates the square of this multivariate polynomial if it is a square.
- Parameters
-
res Used to store the result in.
- Returns
- true, if this multivariate polynomial is a square; false, otherwise.
◆ strip_lterm()
| MultivariatePolynomial& carl::MultivariatePolynomial< Coeff, Ordering, Policies >::strip_lterm | ( | ) |
Drops the leading term.
The function assumes the polynomial to be nonzero, otherwise the leading term is not defined.
- Returns
- A reference to this.
- Todo:
- find new lterm

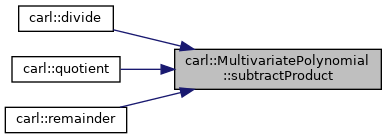
◆ subtractProduct()
| void carl::MultivariatePolynomial< Coeff, Ordering, Policies >::subtractProduct | ( | const Term< Coeff > & | factor, |
| const MultivariatePolynomial< Coeff, Ordering, Policies > & | p | ||
| ) |
Subtract a term times a polynomial from this polynomial.
- Parameters
-
factor Term. p Polynomial.
◆ tail()
| MultivariatePolynomial carl::MultivariatePolynomial< Coeff, Ordering, Policies >::tail | ( | bool | makeFullyOrdered = false | ) | const |
For the polynomial p, the function calculates a polynomial p - lt(p).
The function assumes the polynomial to be nonzero, otherwise, lt(p) is not defined.
- Returns
- A new polynomial p - lt(p).

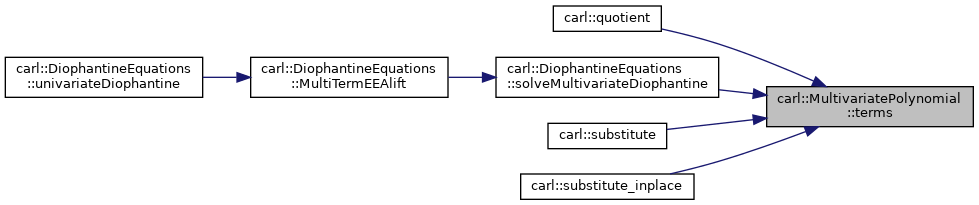
◆ terms() [1/2]
|
inline |
Definition at line 332 of file MultivariatePolynomial.h.
◆ terms() [2/2]
|
inline |
Definition at line 329 of file MultivariatePolynomial.h.
◆ to_integer_domain()
| MultivariatePolynomial<typename IntegralType<Coeff>::type, Ordering, Policies> carl::MultivariatePolynomial< Coeff, Ordering, Policies >::to_integer_domain | ( | ) | const |
◆ total_degree()
| std::size_t carl::MultivariatePolynomial< Coeff, Ordering, Policies >::total_degree | ( | ) | const |
Calculates the max.
degree over all monomials occurring in the polynomial. As the degree of the zero polynomial is ![]() , we assert that this polynomial is not zero. This must be checked by the caller before calling this method.
, we assert that this polynomial is not zero. This must be checked by the caller before calling this method.
- See also
- [3], page 48
- Returns
- Total degree.

◆ trailingTerm() [1/2]
|
inline |
◆ trailingTerm() [2/2]
|
inline |
Give the last term according to Ordering.
Notice that if there is a constant part, it is always trailing.
Definition at line 183 of file MultivariatePolynomial.h.


Friends And Related Function Documentation
◆ operator/ [1/2]
|
friend |
Perform a division involving a polynomial.
- Parameters
-
lhs Left hand side. rhs Right hand side.
- Returns
lhs / rhs
Definition at line 242 of file Division.h.
◆ operator/ [2/2]
|
friend |
Perform a division involving a polynomial.
- Parameters
-
lhs Left hand side. rhs Right hand side.
- Returns
lhs / rhs
◆ operator<<
|
friend |
Definition at line 83 of file MultivariatePolynomial.h.
◆ TermAdditionManager
|
friend |
Definition at line 45 of file MultivariatePolynomial.h.
Field Documentation
◆ has_reasons
|
staticinherited |
Definition at line 31 of file MultivariatePolynomialPolicy.h.
◆ mOrdered
|
mutableprivate |
Flag that indicates if the terms are ordered.
Definition at line 77 of file MultivariatePolynomial.h.
◆ mTermAdditionManager
|
static |
Definition at line 80 of file MultivariatePolynomial.h.
◆ mTerms
|
mutableprivate |
A vector of all terms.
Definition at line 75 of file MultivariatePolynomial.h.
◆ searchLinear
|
staticinherited |
Linear searching means that we search linearly for a term instead of applying e.g.
binary search. Although the worst-case complexity is worse, for polynomials with a small nr of terms, this should be better.
Definition at line 28 of file MultivariatePolynomialPolicy.h.
The documentation for this class was generated from the following files:
- carl-arith/numbers/typetraits.h
- carl-arith/poly/umvpoly/MultivariatePolynomial.h