#include <Contraction.h>
Public Member Functions | |
| VarSolutionFormula ()=delete | |
| VarSolutionFormula (const Polynomial &p, Variable::Arg x) | |
| Constructs the solution formula for the given variable x in the equation p = 0, where p is the given polynomial. More... | |
| void | addRoot (const Interval< double > &_interv, const Interval< double > &_varInterval, std::vector< Interval< double >> &_result) const |
| std::vector< Interval< double > > | evaluate (const Interval< double >::evalintervalmap &intervals) const |
| Evaluates this solution formula for the given mapping of the variables occurring in the solution formula to double intervals. More... | |
Private Attributes | |
| Variable | mVar |
| The variable, for which to solve. More... | |
| uint | mRoot |
| Stores n, if the nth root has to be taken of mNumerator/mDenominator. More... | |
| Polynomial | mNumerator |
| Stores the numerator. More... | |
| std::shared_ptr< const typename Polynomial::MonomType > | mDenominator |
| Stores the denominator, which is one, if mDenominator == nullptr. More... | |
Detailed Description
template<typename Polynomial>
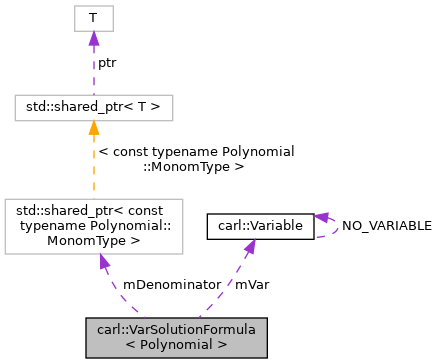
class carl::VarSolutionFormula< Polynomial >
Definition at line 22 of file Contraction.h.
Constructor & Destructor Documentation
◆ VarSolutionFormula() [1/2]
|
delete |
◆ VarSolutionFormula() [2/2]
|
inline |
Constructs the solution formula for the given variable x in the equation p = 0, where p is the given polynomial.
The polynomial p must have one of the following forms: 1.) ax+h, with a being a rational number and h a linear polynomial not containing x and not having a constant part 2.) x^i*m-y, with i being a positive integer, m being a monomial not containing x and y being a variable different from x
- Parameters
-
p The polynomial containing the given variable to construct a solution formula for. x The variable to construct a solution formula for.
Definition at line 48 of file Contraction.h.

Member Function Documentation
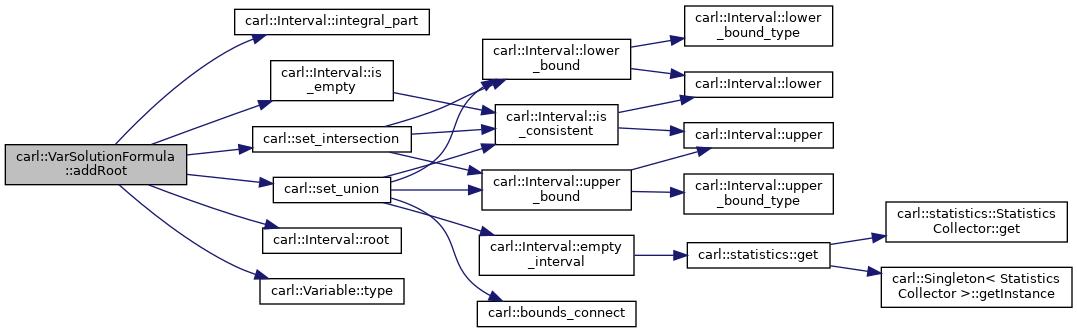
◆ addRoot()
|
inline |
Definition at line 144 of file Contraction.h.

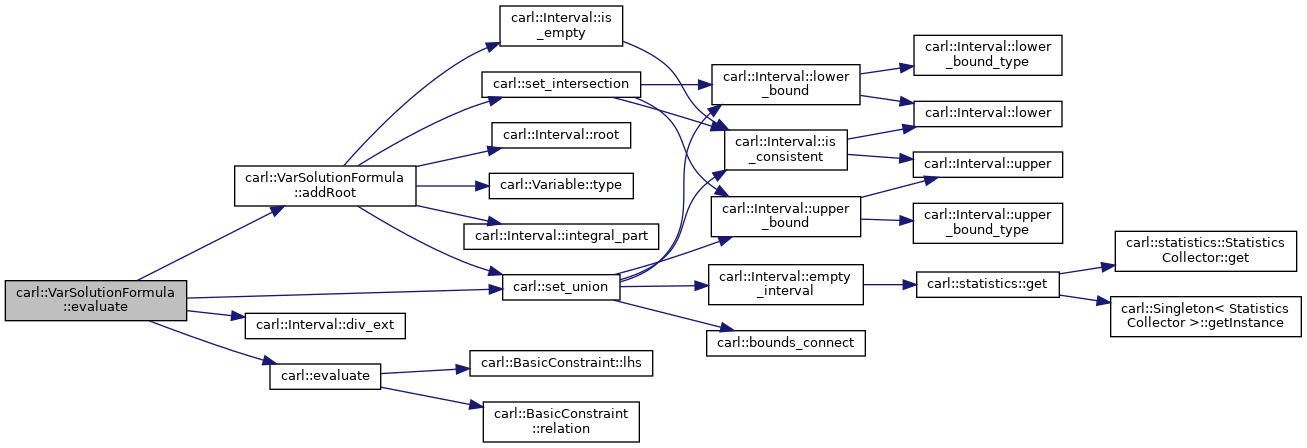
◆ evaluate()
|
inline |
Evaluates this solution formula for the given mapping of the variables occurring in the solution formula to double intervals.
- Parameters
-
intervals The mapping of the variables occurring in the solution formula to double intervals resA The first interval of the result. resB The second interval of the result.
- Returns
- true, if the second interval is not empty. (the first interval must then be also nonempty)
Definition at line 196 of file Contraction.h.
Field Documentation
◆ mDenominator
|
private |
Stores the denominator, which is one, if mDenominator == nullptr.
Definition at line 32 of file Contraction.h.
◆ mNumerator
|
private |
Stores the numerator.
Definition at line 30 of file Contraction.h.
◆ mRoot
|
private |
Stores n, if the nth root has to be taken of mNumerator/mDenominator.
Definition at line 28 of file Contraction.h.
◆ mVar
|
private |
The variable, for which to solve.
Definition at line 26 of file Contraction.h.
The documentation for this class was generated from the following file:
- carl-arith/intervalcontraction/Contraction.h