#include <FactorizedPolynomial.h>
Public Types | |
| enum | ConstructorOperation : unsigned { ADD , SUB , MUL , DIV } |
| using | OrderedBy = typename P::OrderedBy |
| The ordering of the terms. More... | |
| using | CoeffType = typename P::CoeffType |
| Type of the coefficients. More... | |
| using | TermType = typename P::TermType |
| Type of the terms. More... | |
| using | MonomType = typename P::MonomType |
| Type of the monomials within the terms. More... | |
| using | Policy = typename P::Policy |
| Policies for this monomial. More... | |
| using | NumberType = typename UnderlyingNumberType< CoeffType >::type |
| Number type within the coefficients. More... | |
| using | IntNumberType = typename IntegralType< NumberType >::type |
| Integer type associated with the number type. More... | |
| using | PolyType = P |
| using | TermsType = typename P::TermsType |
| using | CACHE = Cache< PolynomialFactorizationPair< P > > |
Public Member Functions | |
| FactorizedPolynomial () | |
| FactorizedPolynomial (const CoeffType &) | |
| FactorizedPolynomial (const P &_polynomial, const std::shared_ptr< CACHE > &, bool _polyNormalized=false) | |
| FactorizedPolynomial (const FactorizedPolynomial< P > &) | |
| FactorizedPolynomial (FactorizedPolynomial< P > &&) | |
| FactorizedPolynomial (const std::pair< ConstructorOperation, std::vector< FactorizedPolynomial >> &_p) | |
| FactorizedPolynomial (Factorization< P > &&_factorization, const CoeffType &, const std::shared_ptr< CACHE > &) | |
| ~FactorizedPolynomial () | |
| FactorizedPolynomial< P > & | operator= (const FactorizedPolynomial< P > &) |
| Copies the given factorized polynomial. More... | |
| operator PolyType () const | |
| CACHE::Ref | cacheRef () const |
| std::shared_ptr< CACHE > | pCache () const |
| CACHE & | cache () const |
| const PolynomialFactorizationPair< P > & | content () const |
| size_t | hash () const |
| void | setCoefficient (CoeffType coeff) const |
| Set coefficient. More... | |
| const Factorization< P > & | factorization () const |
| const P & | polynomial () const |
| const CoeffType & | coefficient () const |
| P | polynomialWithCoefficient () const |
| bool | is_constant () const |
| bool | is_one () const |
| bool | is_zero () const |
| size_t | nr_terms () const |
| Calculates the number of terms. More... | |
| size_t | size () const |
| size_t | complexity () const |
| bool | is_linear () const |
| Checks if the polynomial is linear. More... | |
| template<typename C = CoeffType, EnableIf< is_subset_of_rationals_type< C >> = dummy> | |
| CoeffType | coprime_factor () const |
| template<typename C = CoeffType, EnableIf< is_subset_of_rationals_type< C >> = dummy> | |
| CoeffType | coprime_factor_without_constant () const |
| FactorizedPolynomial< P > | coprime_coefficients () const |
| bool | factorizedTrivially () const |
| void | gatherVariables (std::set< carl::Variable > &_vars) const |
| Iterates through all factors and their terms to find variables occurring in this polynomial. More... | |
| std::set< Variable > | gatherVariables () const |
| CoeffType | constant_part () const |
| Retrieves the constant term of this polynomial or zero, if there is no constant term. More... | |
| size_t | total_degree () const |
| Calculates the max. More... | |
| CoeffType | lcoeff () const |
| Returns the coefficient of the leading term. More... | |
| TermType | lterm () const |
| The leading term. More... | |
| TermType | trailingTerm () const |
| Gives the last term according to Ordering. More... | |
| Variable | single_variable () const |
| For terms with exactly one variable, get this variable. More... | |
| bool | is_univariate () const |
| Checks whether only one variable occurs. More... | |
| UnivariatePolynomial< CoeffType > | toUnivariatePolynomial () const |
| UnivariatePolynomial< FactorizedPolynomial< P > > | toUnivariatePolynomial (Variable _var) const |
| bool | has_constant_term () const |
| Checks if the polynomial has a constant term that is not zero. More... | |
| bool | has (Variable _var) const |
| template<bool gatherCoeff> | |
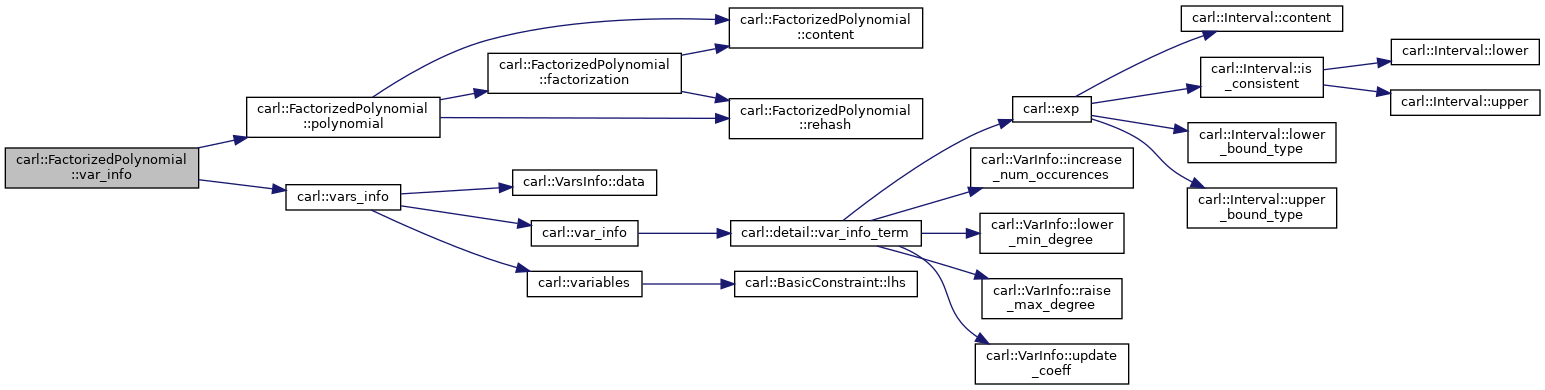
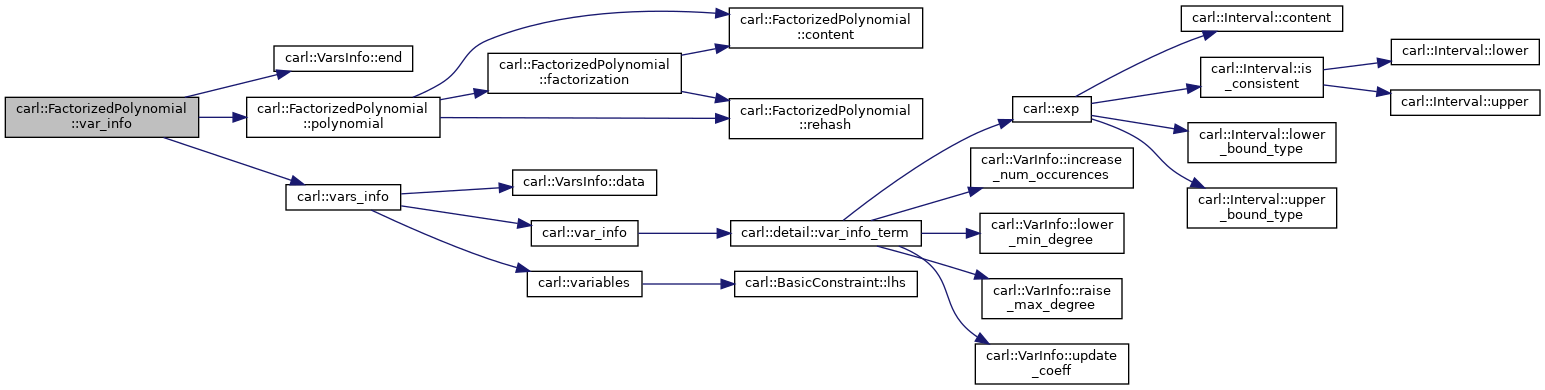
| VarInfo< FactorizedPolynomial< P > > | var_info (Variable _var) const |
| template<bool gatherCoeff> | |
| VarsInfo< FactorizedPolynomial< P > > | var_info () const |
| VarsInfo< FactorizedPolynomial< P > > | var_info () const |
| Definiteness | definiteness (bool _fullEffort=true) const |
| Retrieves information about the definiteness of the polynomial. More... | |
| FactorizedPolynomial< P > | derivative (const carl::Variable &_var, unsigned _nth=1) const |
| Derivative of the factorized polynomial wrt variable x. More... | |
| FactorizedPolynomial< P > | pow (unsigned _exp) const |
| Raise polynomial to the power. More... | |
| bool | sqrt (FactorizedPolynomial< P > &_result) const |
| Calculates the square of this factorized polynomial if it is a square. More... | |
| template<typename C = CoeffType, EnableIf< is_field_type< C >> = dummy> | |
| FactorizedPolynomial< P > | divideBy (const CoeffType &_divisor) const |
| Divides the polynomial by the given coefficient. More... | |
| DivisionResult< FactorizedPolynomial< P > > | divideBy (const FactorizedPolynomial< P > &_divisor) const |
| Calculating the quotient and the remainder, such that for a given polynomial p we have p = _divisor * quotient + remainder. More... | |
| template<typename C = CoeffType, EnableIf< is_field_type< C >> = dummy> | |
| bool | divideBy (const FactorizedPolynomial< P > &_divisor, FactorizedPolynomial< P > &_quotient) const |
| Divides the polynomial by another polynomial. More... | |
| FactorizedPolynomial< P > | operator- () const |
| FactorizedPolynomial< P > & | operator+= (const CoeffType &_coef) |
| FactorizedPolynomial< P > & | operator+= (const FactorizedPolynomial< P > &_fpoly) |
| FactorizedPolynomial< P > & | operator-= (const CoeffType &_coef) |
| FactorizedPolynomial< P > & | operator-= (const FactorizedPolynomial< P > &_fpoly) |
| FactorizedPolynomial< P > & | operator*= (const CoeffType &_coef) |
| FactorizedPolynomial< P > & | operator*= (const FactorizedPolynomial< P > &_fpoly) |
| FactorizedPolynomial< P > & | operator/= (const CoeffType &_coef) |
| Calculates the quotient. More... | |
| FactorizedPolynomial< P > & | operator/= (const FactorizedPolynomial< P > &_fpoly) |
| Calculates the quotient. More... | |
| FactorizedPolynomial< P > | quotient (const FactorizedPolynomial< P > &_fdivisor) const |
| Calculates the quotient. More... | |
| std::string | toString (bool _infix=true, bool _friendlyVarNames=true) const |
Static Public Member Functions | |
| static std::shared_ptr< CACHE > | chooseCache (std::shared_ptr< CACHE > _pCacheA, std::shared_ptr< CACHE > _pCacheB) |
| Choose a non-null cache from two caches. More... | |
Private Member Functions | |
| void | rehash () const |
| Updates the hash of the entry in the cache corresponding to this factorized polynomial, which is also its hash. More... | |
| void | strengthenActivity () const |
Private Attributes | |
| CACHE::Ref | mCacheRef |
| The reference of the entry in the cache corresponding to this factorized polynomial. More... | |
| std::shared_ptr< CACHE > | mpCache |
| The cache in which the actual content of this factorized polynomial is stored. More... | |
| CoeffType | mCoefficient |
| Co-prime coefficient of the factorization. More... | |
Friends | |
| template<typename P1 > | |
| Factorization< P1 > | gcd (const PolynomialFactorizationPair< P1 > &_pfPairA, const PolynomialFactorizationPair< P1 > &_pfPairB, Factorization< P1 > &_restA, Factorization< P1 > &_rest2B, bool &_pfPairARefined, bool &_pfPairBRefined) |
| template<typename P1 > | |
| bool | existsFactorization (const FactorizedPolynomial< P1 > &fpoly) |
| template<typename P1 > | |
| Coeff< P1 > | distributeCoefficients (Factorization< P1 > &_factorization) |
| Computes the coefficient of the factorization and sets the coefficients of all factors to 1. More... | |
| template<typename P1 > | |
| Factorization< P1 > | commonDivisor (const FactorizedPolynomial< P1 > &_fFactorizationA, const FactorizedPolynomial< P1 > &_fFactorizationB, Factorization< P1 > &_fFactorizationRestA, Factorization< P1 > &_fFactorizationRestB) |
| Computes the common divisor with rest of two factorizations. More... | |
| template<typename P1 > | |
| FactorizedPolynomial< P1 > | gcd (const FactorizedPolynomial< P1 > &_fpolyA, const FactorizedPolynomial< P1 > &_fpolyB, FactorizedPolynomial< P1 > &_fpolyRestA, FactorizedPolynomial< P1 > &_fpolyRestB) |
| Determines the greatest common divisor of the two given factorized polynomials. More... | |
| template<typename P1 > | |
| P1 | computePolynomial (const FactorizedPolynomial< P1 > &_fpoly) |
| template<typename P1 > | |
| FactorizedPolynomial< P1 > | quotient (const FactorizedPolynomial< P1 > &_fpolyA, const FactorizedPolynomial< P1 > &_fpolyB) |
| Calculates the quotient of the polynomials. More... | |
| template<typename P1 > | |
| FactorizedPolynomial< P1 > | lcm (const FactorizedPolynomial< P1 > &_fpolyA, const FactorizedPolynomial< P1 > &_fpolyB) |
| Computes the least common multiple of two given polynomials. More... | |
| template<typename P1 > | |
| FactorizedPolynomial< P1 > | commonDivisor (const FactorizedPolynomial< P1 > &_fpolyA, const FactorizedPolynomial< P1 > &_fpolyB) |
| template<typename P1 > | |
| FactorizedPolynomial< P1 > | commonMultiple (const FactorizedPolynomial< P1 > &_fpolyA, const FactorizedPolynomial< P1 > &_fpolyB) |
| template<typename P1 > | |
| FactorizedPolynomial< P1 > | gcd (const FactorizedPolynomial< P1 > &_fpolyA, const FactorizedPolynomial< P1 > &_fpolyB) |
| Determines the greatest common divisor of the two given factorized polynomials. More... | |
| template<typename P1 > | |
| std::pair< FactorizedPolynomial< P1 >, FactorizedPolynomial< P1 > > | lazyDiv (const FactorizedPolynomial< P1 > &_fpolyA, const FactorizedPolynomial< P1 > &_fpolyB) |
| Divides each of the two given factorized polynomials by their common factors of their (partial) factorization. More... | |
| template<typename P1 > | |
| Factors< FactorizedPolynomial< P1 > > | factor (const FactorizedPolynomial< P1 > &_fpoly) |
| template<typename P1 > | |
| FactorizedPolynomial< P1 > | operator+ (const FactorizedPolynomial< P1 > &_lhs, const FactorizedPolynomial< P1 > &_rhs) |
| template<typename P1 > | |
| FactorizedPolynomial< P1 > | operator+ (const FactorizedPolynomial< P1 > &_lhs, const typename FactorizedPolynomial< P1 >::CoeffType &_rhs) |
| template<typename P1 > | |
| FactorizedPolynomial< P1 > | operator- (const FactorizedPolynomial< P1 > &_lhs, const FactorizedPolynomial< P1 > &_rhs) |
| template<typename P1 > | |
| FactorizedPolynomial< P1 > | operator- (const FactorizedPolynomial< P1 > &_lhs, const typename FactorizedPolynomial< P1 >::CoeffType &_rhs) |
| template<typename P1 > | |
| FactorizedPolynomial< P1 > | operator* (const FactorizedPolynomial< P1 > &_lhs, const FactorizedPolynomial< P1 > &_rhs) |
| template<typename P1 > | |
| FactorizedPolynomial< P1 > | operator* (const FactorizedPolynomial< P1 > &_lhs, const typename FactorizedPolynomial< P1 >::CoeffType &_rhs) |
Detailed Description
template<typename P>
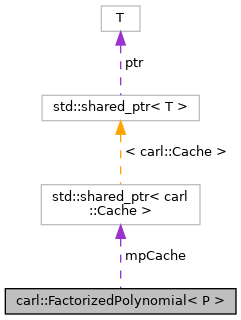
class carl::FactorizedPolynomial< P >
Definition at line 23 of file FactorizedPolynomial.h.
Member Typedef Documentation
◆ CACHE
| using carl::FactorizedPolynomial< P >::CACHE = Cache<PolynomialFactorizationPair<P> > |
Definition at line 48 of file FactorizedPolynomial.h.
◆ CoeffType
| using carl::FactorizedPolynomial< P >::CoeffType = typename P::CoeffType |
Type of the coefficients.
Definition at line 32 of file FactorizedPolynomial.h.
◆ IntNumberType
| using carl::FactorizedPolynomial< P >::IntNumberType = typename IntegralType<NumberType>::type |
Integer type associated with the number type.
Definition at line 42 of file FactorizedPolynomial.h.
◆ MonomType
| using carl::FactorizedPolynomial< P >::MonomType = typename P::MonomType |
Type of the monomials within the terms.
Definition at line 36 of file FactorizedPolynomial.h.
◆ NumberType
| using carl::FactorizedPolynomial< P >::NumberType = typename UnderlyingNumberType<CoeffType>::type |
Number type within the coefficients.
Definition at line 40 of file FactorizedPolynomial.h.
◆ OrderedBy
| using carl::FactorizedPolynomial< P >::OrderedBy = typename P::OrderedBy |
The ordering of the terms.
Definition at line 30 of file FactorizedPolynomial.h.
◆ Policy
| using carl::FactorizedPolynomial< P >::Policy = typename P::Policy |
Policies for this monomial.
Definition at line 38 of file FactorizedPolynomial.h.
◆ PolyType
| using carl::FactorizedPolynomial< P >::PolyType = P |
Definition at line 44 of file FactorizedPolynomial.h.
◆ TermsType
| using carl::FactorizedPolynomial< P >::TermsType = typename P::TermsType |
Definition at line 46 of file FactorizedPolynomial.h.
◆ TermType
| using carl::FactorizedPolynomial< P >::TermType = typename P::TermType |
Type of the terms.
Definition at line 34 of file FactorizedPolynomial.h.
Member Enumeration Documentation
◆ ConstructorOperation
| enum carl::FactorizedPolynomial::ConstructorOperation : unsigned |
| Enumerator | |
|---|---|
| ADD | |
| SUB | |
| MUL | |
| DIV | |
Definition at line 50 of file FactorizedPolynomial.h.
Constructor & Destructor Documentation
◆ FactorizedPolynomial() [1/7]
| carl::FactorizedPolynomial< P >::FactorizedPolynomial | ( | ) |
◆ FactorizedPolynomial() [2/7]
|
explicit |
◆ FactorizedPolynomial() [3/7]
|
explicit |
◆ FactorizedPolynomial() [4/7]
| carl::FactorizedPolynomial< P >::FactorizedPolynomial | ( | const FactorizedPolynomial< P > & | ) |
◆ FactorizedPolynomial() [5/7]
| carl::FactorizedPolynomial< P >::FactorizedPolynomial | ( | FactorizedPolynomial< P > && | ) |
◆ FactorizedPolynomial() [6/7]
|
explicit |
◆ FactorizedPolynomial() [7/7]
|
explicit |
◆ ~FactorizedPolynomial()
| carl::FactorizedPolynomial< P >::~FactorizedPolynomial | ( | ) |
Member Function Documentation
◆ cache()
|
inline |
- Returns
- The cache used by this factorized polynomial.
Definition at line 175 of file FactorizedPolynomial.h.
◆ cacheRef()
|
inline |
- Returns
- The reference of the entry in the cache corresponding to this factorized polynomial.
Definition at line 159 of file FactorizedPolynomial.h.
◆ chooseCache()
|
inlinestatic |
Choose a non-null cache from two caches.
- Parameters
-
_pCacheA First cache. _pCacheB Second cache.
- Returns
- A non-null cache.
Definition at line 591 of file FactorizedPolynomial.h.
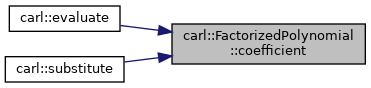
◆ coefficient()
|
inline |
- Returns
- Coefficient of the polynomial.
Definition at line 242 of file FactorizedPolynomial.h.
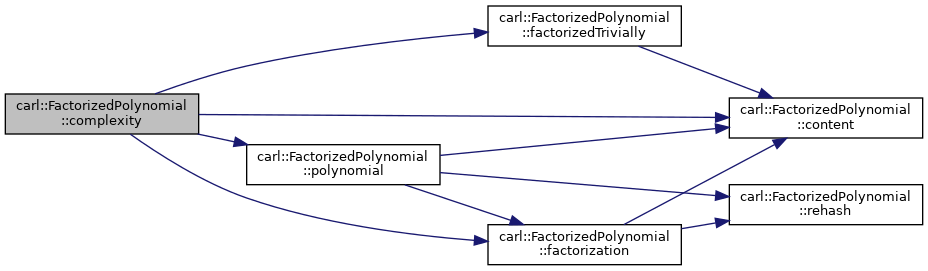
◆ complexity()
|
inline |
- Returns
- An approximation of the complexity of this polynomial.
Definition at line 312 of file FactorizedPolynomial.h.
◆ constant_part()
| CoeffType carl::FactorizedPolynomial< P >::constant_part | ( | ) | const |
Retrieves the constant term of this polynomial or zero, if there is no constant term.
@reiturn Constant term.

◆ content()
|
inline |
- Returns
- The entry in the cache corresponding to this factorized polynomial.
Definition at line 183 of file FactorizedPolynomial.h.

◆ coprime_coefficients()
|
inline |
- Returns
- p * p.coprime_factor()
- See also
- coprime_factor()
Definition at line 362 of file FactorizedPolynomial.h.

◆ coprime_factor()
|
inline |
- Returns
- The lcm of the denominators of the coefficients in p divided by the gcd of numerators of the coefficients in p.
Definition at line 346 of file FactorizedPolynomial.h.

◆ coprime_factor_without_constant()
| CoeffType carl::FactorizedPolynomial< P >::coprime_factor_without_constant | ( | ) | const |
- Returns
- The lcm of the denominators of the coefficients (without the constant one) in p divided by the gcd of numerators of the coefficients in p.
◆ definiteness()
| Definiteness carl::FactorizedPolynomial< P >::definiteness | ( | bool | _fullEffort = true | ) | const |
Retrieves information about the definiteness of the polynomial.
- Returns
- Definiteness of this.
◆ derivative()
| FactorizedPolynomial<P> carl::FactorizedPolynomial< P >::derivative | ( | const carl::Variable & | _var, |
| unsigned | _nth = 1 |
||
| ) | const |
Derivative of the factorized polynomial wrt variable x.
- Parameters
-
_var main variable _nth how often should derivative be applied
- Todo:
only _nth == 1 is supported
we do not use factorization currently
◆ divideBy() [1/3]
| FactorizedPolynomial<P> carl::FactorizedPolynomial< P >::divideBy | ( | const CoeffType & | _divisor | ) | const |
Divides the polynomial by the given coefficient.
Applies if the coefficients are from a field.
- Parameters
-
_divisor
- Returns
◆ divideBy() [2/3]
| DivisionResult<FactorizedPolynomial<P> > carl::FactorizedPolynomial< P >::divideBy | ( | const FactorizedPolynomial< P > & | _divisor | ) | const |
Calculating the quotient and the remainder, such that for a given polynomial p we have p = _divisor * quotient + remainder.
- Parameters
-
_divisor Another polynomial
- Returns
- A divisionresult, holding the quotient and the remainder.
- See also
- Note
- Division is only defined on fields
◆ divideBy() [3/3]
| bool carl::FactorizedPolynomial< P >::divideBy | ( | const FactorizedPolynomial< P > & | _divisor, |
| FactorizedPolynomial< P > & | _quotient | ||
| ) | const |
Divides the polynomial by another polynomial.
If the divisor divides this polynomial, quotient contains the result of the division and true is returned. Otherwise, false is returned and the content of quotient remains unchanged. Applies if the coefficients are from a field. Note that the quotient must not be *this.
- Parameters
-
_divisor _quotient
- Returns
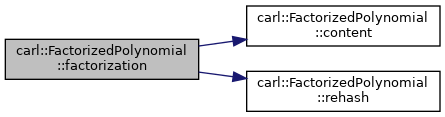
◆ factorization()
|
inline |
- Returns
- The factorization of this polynomial.
Definition at line 214 of file FactorizedPolynomial.h.

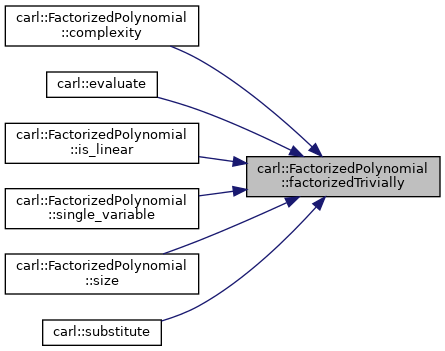
◆ factorizedTrivially()
|
inline |
- Returns
- true, if this factorized polynomial, has only itself as factor.
Definition at line 376 of file FactorizedPolynomial.h.

◆ gatherVariables() [1/2]
|
inline |
Definition at line 392 of file FactorizedPolynomial.h.
◆ gatherVariables() [2/2]
|
inline |
Iterates through all factors and their terms to find variables occurring in this polynomial.
- Parameters
-
vars Holds the variables occurring in the polynomial at return.
Definition at line 385 of file FactorizedPolynomial.h.

◆ has()
| bool carl::FactorizedPolynomial< P >::has | ( | Variable | _var | ) | const |
- Parameters
-
_var The variable to check for its occurrence.
- Returns
- true, if the variable occurs in this term.
◆ has_constant_term()
| bool carl::FactorizedPolynomial< P >::has_constant_term | ( | ) | const |
Checks if the polynomial has a constant term that is not zero.
- Returns
- If there is a constant term unequal to zero.
◆ hash()
|
inline |
- Returns
- The hash value of the entry in the cache corresponding to this factorized polynomial.
Definition at line 192 of file FactorizedPolynomial.h.

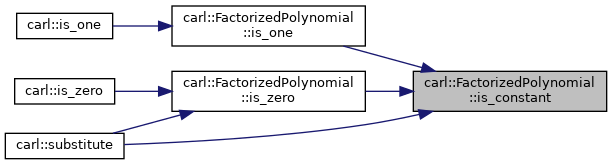
◆ is_constant()
|
inline |
- Returns
- true, if the factorized polynomial is constant.
Definition at line 260 of file FactorizedPolynomial.h.
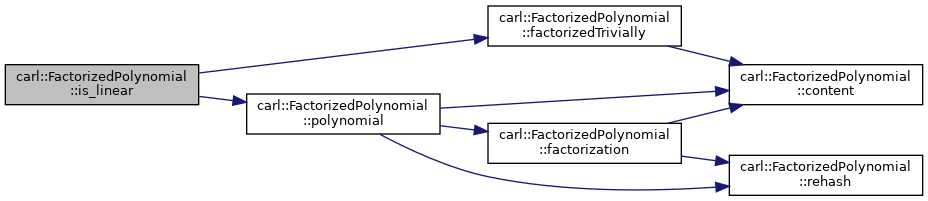
◆ is_linear()
|
inline |
Checks if the polynomial is linear.
- Returns
- If this is linear.
Definition at line 330 of file FactorizedPolynomial.h.
◆ is_one()
|
inline |
- Returns
- true, if the factorized polynomial is one.
Definition at line 268 of file FactorizedPolynomial.h.


◆ is_univariate()
| bool carl::FactorizedPolynomial< P >::is_univariate | ( | ) | const |
Checks whether only one variable occurs.
- Returns
- Notice that it might be better to use the variable information if several pieces of information are requested.
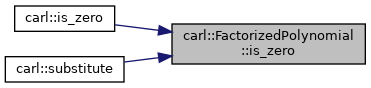
◆ is_zero()
|
inline |
- Returns
- true, if the factorized polynomial is zero.
Definition at line 276 of file FactorizedPolynomial.h.

◆ lcoeff()
| CoeffType carl::FactorizedPolynomial< P >::lcoeff | ( | ) | const |
Returns the coefficient of the leading term.
Notice that this is not defined for zero polynomials.
- Returns
◆ lterm()
| TermType carl::FactorizedPolynomial< P >::lterm | ( | ) | const |
The leading term.
- Returns
◆ nr_terms()
|
inline |
Calculates the number of terms.
(Note, that this requires to expand the factorization and, thus, can be expensive in the case that the factorization has not yet been expanded.)
- Returns
- the number of terms
Definition at line 286 of file FactorizedPolynomial.h.

◆ operator PolyType()
|
inlineexplicit |
◆ operator*=() [1/2]
| FactorizedPolynomial<P>& carl::FactorizedPolynomial< P >::operator*= | ( | const CoeffType & | _coef | ) |
- Parameters
-
_coef The factor to multiply this factorized polynomial with.
- Returns
- This factorized polynomial after multiplying it with the given factor.
◆ operator*=() [2/2]
| FactorizedPolynomial<P>& carl::FactorizedPolynomial< P >::operator*= | ( | const FactorizedPolynomial< P > & | _fpoly | ) |
- Parameters
-
_fpoly The factor to multiply this factorized polynomial with.
- Returns
- This factorized polynomial after multiplying it with the given factor.
◆ operator+=() [1/2]
| FactorizedPolynomial<P>& carl::FactorizedPolynomial< P >::operator+= | ( | const CoeffType & | _coef | ) |
- Parameters
-
_coef The summand to add this factorized polynomial with.
- Returns
- This factorized polynomial after adding the given summand.
◆ operator+=() [2/2]
| FactorizedPolynomial<P>& carl::FactorizedPolynomial< P >::operator+= | ( | const FactorizedPolynomial< P > & | _fpoly | ) |
- Parameters
-
_fpoly The summand to add this factorized polynomial with.
- Returns
- This factorized polynomial after adding the given summand.
◆ operator-()
| FactorizedPolynomial<P> carl::FactorizedPolynomial< P >::operator- | ( | ) | const |
- Parameters
-
_fpoly The operand.
- Returns
- The given factorized polynomial times -1.
◆ operator-=() [1/2]
| FactorizedPolynomial<P>& carl::FactorizedPolynomial< P >::operator-= | ( | const CoeffType & | _coef | ) |
- Parameters
-
_coef The number to subtract from this factorized polynomial.
- Returns
- This factorized polynomial after subtracting the given number.
◆ operator-=() [2/2]
| FactorizedPolynomial<P>& carl::FactorizedPolynomial< P >::operator-= | ( | const FactorizedPolynomial< P > & | _fpoly | ) |
- Parameters
-
_fpoly The factorized polynomial to subtract from this factorized polynomial.
- Returns
- This factorized polynomial after adding the given factorized polynomial.
◆ operator/=() [1/2]
| FactorizedPolynomial<P>& carl::FactorizedPolynomial< P >::operator/= | ( | const CoeffType & | _coef | ) |
Calculates the quotient.
Notice: the divisor has to be a factor of the polynomial.
- Parameters
-
_coef The divisor to divide this factorized polynomial with.
- Returns
- This factorized polynomial after dividing it with the given divisor.
◆ operator/=() [2/2]
| FactorizedPolynomial<P>& carl::FactorizedPolynomial< P >::operator/= | ( | const FactorizedPolynomial< P > & | _fpoly | ) |
Calculates the quotient.
Notice: the divisor has to be a factor of the polynomial.
- Parameters
-
_fpoly The divisor to divide this factorized polynomial with.
- Returns
- This factorized polynomial after dividing it with the given divisor.
◆ operator=()
| FactorizedPolynomial<P>& carl::FactorizedPolynomial< P >::operator= | ( | const FactorizedPolynomial< P > & | ) |
Copies the given factorized polynomial.
- Parameters
-
The factorized polynomial to copy.
- Returns
- A reference to the copy of the given factorized polynomial.
◆ pCache()
|
inline |
- Returns
- The cache used by this factorized polynomial.
Definition at line 167 of file FactorizedPolynomial.h.

◆ polynomial()
|
inline |
Definition at line 227 of file FactorizedPolynomial.h.


◆ polynomialWithCoefficient()
|
inline |
◆ pow()
| FactorizedPolynomial<P> carl::FactorizedPolynomial< P >::pow | ( | unsigned | _exp | ) | const |
Raise polynomial to the power.
- Parameters
-
_exp the exponent of the power
- Returns
- p^exponent
- Todo:
- uses multiplication -> bad idea.
◆ quotient()
| FactorizedPolynomial<P> carl::FactorizedPolynomial< P >::quotient | ( | const FactorizedPolynomial< P > & | _fdivisor | ) | const |
Calculates the quotient.
Notice: the divisor has to be a factor of the polynomial.
- Parameters
-
_fdivisor The divisor
- Returns
- The quotient
◆ rehash()
|
inlineprivate |
Updates the hash of the entry in the cache corresponding to this factorized polynomial, which is also its hash.
Definition at line 74 of file FactorizedPolynomial.h.

◆ setCoefficient()
|
inline |
Set coefficient.
- Parameters
-
coeff Coefficient
Definition at line 206 of file FactorizedPolynomial.h.

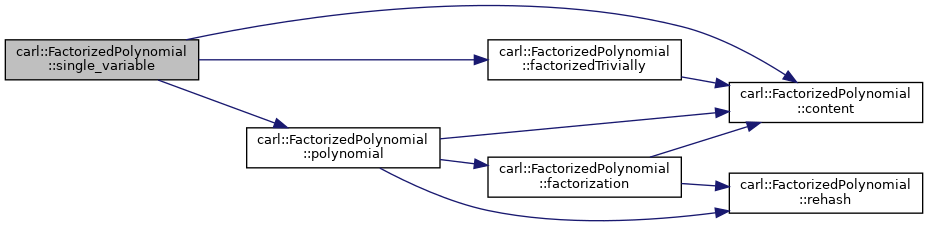
◆ single_variable()
|
inline |
For terms with exactly one variable, get this variable.
- Returns
- The only variable occuring in the term.
Definition at line 436 of file FactorizedPolynomial.h.
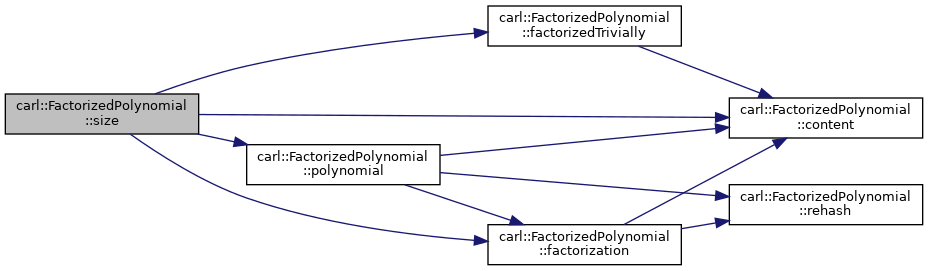
◆ size()
|
inline |
- Returns
- A rough estimation of the size of this factorized polynomial. If it has already been expanded, the number of terms of the expanded form are returned; otherwise the number of terms in the factors.
Definition at line 295 of file FactorizedPolynomial.h.
◆ sqrt()
| bool carl::FactorizedPolynomial< P >::sqrt | ( | FactorizedPolynomial< P > & | _result | ) | const |
Calculates the square of this factorized polynomial if it is a square.
- Parameters
-
_result Used to store the result in.
- Returns
- true, if this factorized polynomial is a square; false, otherwise.
◆ strengthenActivity()
|
inlineprivate |
Definition at line 80 of file FactorizedPolynomial.h.
◆ toString()
| std::string carl::FactorizedPolynomial< P >::toString | ( | bool | _infix = true, |
| bool | _friendlyVarNames = true |
||
| ) | const |
- Parameters
-
_infix _friendlyVarNames
- Returns
◆ total_degree()
| size_t carl::FactorizedPolynomial< P >::total_degree | ( | ) | const |
Calculates the max.
degree over all monomials occurring in the polynomial. As the degree of the zero polynomial is ![]() , we assert that this polynomial is not zero. This must be checked by the caller before calling this method.
, we assert that this polynomial is not zero. This must be checked by the caller before calling this method.
- See also
- [3], page 48
- Returns
- Total degree.
◆ toUnivariatePolynomial() [1/2]
|
inline |
◆ toUnivariatePolynomial() [2/2]
| UnivariatePolynomial<FactorizedPolynomial<P> > carl::FactorizedPolynomial< P >::toUnivariatePolynomial | ( | Variable | _var | ) | const |
◆ trailingTerm()
| TermType carl::FactorizedPolynomial< P >::trailingTerm | ( | ) | const |
Gives the last term according to Ordering.
Notice that if there is a constant part, it is always trailing.
- Returns
◆ var_info() [1/3]
|
inline |
◆ var_info() [2/3]
|
inline |
◆ var_info() [3/3]
| VarInfo<FactorizedPolynomial<P> > carl::FactorizedPolynomial< P >::var_info | ( | Variable | _var | ) | const |
Friends And Related Function Documentation
◆ commonDivisor [1/2]
|
friend |
Computes the common divisor with rest of two factorizations.
- Parameters
-
_fFactorizationA The factorization of the first polynomial. _fFactorizationB The factorization of the second polynomial. _fFactorizationRestA Returns the remaining factorization of the first polynomial without the common divisor _fFactorizationRestB Returns the remaining factorization of the second polynomial without the common divisor
- Returns
- The factorization of a common divisor of the two given factorized polynomials.
◆ commonDivisor [2/2]
|
friend |
- Parameters
-
_fpolyA The first factorized polynomial to compute the common divisor for. _fpolyB The second factorized polynomial to compute the common divisor for.
- Returns
- A common divisor of the two given factorized polynomials.
◆ commonMultiple
|
friend |
- Parameters
-
_fpolyA The first factorized polynomial to compute the common multiple for. _fpolyB The second factorized polynomial to compute the common multiple for.
- Returns
- A common multiple of the two given factorized polynomials.
◆ computePolynomial
|
friend |
- Parameters
-
_fpoly The factorized polynomial to retrieve the expanded polynomial for.
- Returns
- The polynomial (of the underlying polynomial type) when expanding the factorization of the given factorized polynomial.
◆ distributeCoefficients
|
friend |
Computes the coefficient of the factorization and sets the coefficients of all factors to 1.
- Parameters
-
_factorization The factorization.
- Returns
- The coefficients of the whole factorization.
◆ existsFactorization
|
friend |
Definition at line 87 of file FactorizedPolynomial.h.
◆ factor
|
friend |
- Parameters
-
_fpoly The polynomial to calculate the factorization for.
- Returns
- A factorization of this factorized polynomial. (probably finer than the one factorization() returns)
◆ gcd [1/3]
|
friend |
Determines the greatest common divisor of the two given factorized polynomials.
The method exploits the partial factorization stored in the arguments and refines it. (c.f. Accelerating Parametric Probabilistic Verification, Section 4)
- Parameters
-
_fpolyA The first factorized polynomial to compute the greatest common divisor for. _fpolyB The second factorized polynomial to compute the greatest common divisor for.
- Returns
- The greatest common divisor of the two given factorized polynomials.
◆ gcd [2/3]
|
friend |
Determines the greatest common divisor of the two given factorized polynomials.
The method exploits the partial factorization stored in the arguments and refines it. (c.f. Accelerating Parametric Probabilistic Verification, Section 4)
- Parameters
-
_fpolyA The first factorized polynomial to compute the greatest common divisor for. _fpolyB The second factorized polynomial to compute the greatest common divisor for. _fpolyRestA Returns the remaining part of the first factorized polynomial without the gcd. _fpolyRestB Returns the remaining part of the second factorized polynomial without the gcd.
- Returns
- The greatest common divisor of the two given factorized polynomials.
◆ gcd [3/3]
|
friend |
◆ lazyDiv
|
friend |
Divides each of the two given factorized polynomials by their common factors of their (partial) factorization.
- Parameters
-
_fpolyA The first factorized polynomial. _fpolyB The second factorized polynomial.
- Returns
- The pair of the resulting factorized polynomials.
◆ lcm
|
friend |
Computes the least common multiple of two given polynomials.
The method refines the factorization.
- Parameters
-
_fpolyA The first factorized polynomial to compute the lcm for. _fpolyB The second factorized polynomial to compute the lcm for.
- Returns
- The lcm of the two given factorized polynomials.
◆ operator* [1/2]
|
friend |
◆ operator* [2/2]
|
friend |
◆ operator+ [1/2]
|
friend |
◆ operator+ [2/2]
|
friend |
◆ operator- [1/2]
|
friend |
◆ operator- [2/2]
|
friend |
◆ quotient
|
friend |
Calculates the quotient of the polynomials.
Notice: the second polynomial has to be a factor of the first polynomial.
- Parameters
-
_fpolyA The dividend. _fpolyB The divisor.
- Returns
- The quotient
Field Documentation
◆ mCacheRef
|
mutableprivate |
The reference of the entry in the cache corresponding to this factorized polynomial.
Definition at line 58 of file FactorizedPolynomial.h.
◆ mCoefficient
|
mutableprivate |
Co-prime coefficient of the factorization.
Definition at line 68 of file FactorizedPolynomial.h.
◆ mpCache
|
private |
The cache in which the actual content of this factorized polynomial is stored.
Definition at line 63 of file FactorizedPolynomial.h.
The documentation for this class was generated from the following file:
- carl-extpolys/FactorizedPolynomial.h