carl::ran::interval Namespace Reference

Namespaces
	detail_field_extensions

Data Structures
class	FieldExtensions
	This class can be used to construct iterated field extensions from a sequence of real algebraic numbers. More...
class	LazardEvaluation
class	RealRootIsolation
	Compact class to isolate real roots from a univariate polynomial using bisection. More...
class	ran_evaluator

Enumerations
enum class	AlgebraicSubstitutionStrategy { RESULTANT , GROEBNER }
	Indicates which strategy to use: resultants or Gröbner bases. More...

Functions
template<typename Number >
std::optional< UnivariatePolynomial< Number > >	algebraic_substitution_groebner (const std::vector< MultivariatePolynomial< Number >> &polynomials, const std::vector< Variable > &variables)
	Implements algebraic substitution by Gröbner basis computation. More...
template<typename Number >
std::optional< UnivariatePolynomial< Number > >	algebraic_substitution_groebner (const UnivariatePolynomial< MultivariatePolynomial< Number >> &p, const std::vector< UnivariatePolynomial< MultivariatePolynomial< Number >>> &polynomials)
	Implements algebraic substitution by Gröbner basis computation. More...
template<typename Number >
std::optional< UnivariatePolynomial< Number > >	algebraic_substitution_resultant (const UnivariatePolynomial< MultivariatePolynomial< Number >> &p, const std::vector< UnivariatePolynomial< MultivariatePolynomial< Number >>> &polynomials)
	Implements algebraic substitution by resultant computation. More...
template<typename Number >
std::optional< UnivariatePolynomial< Number > >	algebraic_substitution_resultant (const std::vector< MultivariatePolynomial< Number >> &polynomials, const std::vector< Variable > &variables)
	Implements algebraic substitution by resultant computation. More...
template<typename Number >
std::optional< UnivariatePolynomial< Number > >	algebraic_substitution (const UnivariatePolynomial< MultivariatePolynomial< Number >> &p, const std::vector< UnivariatePolynomial< MultivariatePolynomial< Number >>> &polynomials, AlgebraicSubstitutionStrategy strategy=AlgebraicSubstitutionStrategy::RESULTANT)
	Computes the algebraic substitution of the given defining polynomials into a multivariate polynomial p. More...
template<typename Number >
std::optional< UnivariatePolynomial< Number > >	algebraic_substitution (const std::vector< MultivariatePolynomial< Number >> &polynomials, const std::vector< Variable > &variables, AlgebraicSubstitutionStrategy strategy=AlgebraicSubstitutionStrategy::RESULTANT)
	Computes the algebraic substitution of the given defining polynomials into a multivariate polynomial p. More...
template<typename Number , typename Coeff >
std::optional< UnivariatePolynomial< Number > >	substitute_rans_into_polynomial (const UnivariatePolynomial< Coeff > &p, const OrderedAssignment< IntRepRealAlgebraicNumber< Number >> &m, bool use_lazard=false)

Enumeration Type Documentation

AlgebraicSubstitutionStrategy

enum carl::ran::interval::AlgebraicSubstitutionStrategy

strong

Indicates which strategy to use: resultants or Gröbner bases.

Enumerator
RESULTANT
GROEBNER

Definition at line 145 of file AlgebraicSubstitution.h.

Function Documentation

algebraic_substitution() [1/2]

template<typename Number >

std::optional<UnivariatePolynomial<Number> > carl::ran::interval::algebraic_substitution	(	const std::vector< MultivariatePolynomial< Number >> &	polynomials,
		const std::vector< Variable > &	variables,
		AlgebraicSubstitutionStrategy	strategy = AlgebraicSubstitutionStrategy::RESULTANT
	)

Computes the algebraic substitution of the given defining polynomials into a multivariate polynomial p.

The result is a univariate polynomial in the main variable of p.

Definition at line 174 of file AlgebraicSubstitution.h.

Here is the call graph for this function:

algebraic_substitution() [2/2]

template<typename Number >

std::optional<UnivariatePolynomial<Number> > carl::ran::interval::algebraic_substitution	(	const UnivariatePolynomial< MultivariatePolynomial< Number >> &	p,
		const std::vector< UnivariatePolynomial< MultivariatePolynomial< Number >>> &	polynomials,
		AlgebraicSubstitutionStrategy	strategy = AlgebraicSubstitutionStrategy::RESULTANT
	)

Computes the algebraic substitution of the given defining polynomials into a multivariate polynomial p.

The result is a univariate polynomial in the main variable of p.

Definition at line 154 of file AlgebraicSubstitution.h.

Here is the call graph for this function:

Here is the caller graph for this function:

algebraic_substitution_groebner() [1/2]

template<typename Number >

std::optional<UnivariatePolynomial<Number> > carl::ran::interval::algebraic_substitution_groebner	(	const std::vector< MultivariatePolynomial< Number >> &	polynomials,
		const std::vector< Variable > &	variables
	)

Implements algebraic substitution by Gröbner basis computation.

Essentially we take all polynomials and compute a Gröbner basis with respect to an elimination order, having the remaining variable at the end. The result is then the polynomial in the last variable only.

Definition at line 37 of file AlgebraicSubstitution.h.

Here is the call graph for this function:

Here is the caller graph for this function:

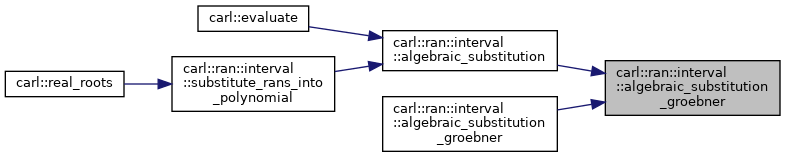
algebraic_substitution_groebner() [2/2]

template<typename Number >

std::optional<UnivariatePolynomial<Number> > carl::ran::interval::algebraic_substitution_groebner	(	const UnivariatePolynomial< MultivariatePolynomial< Number >> &	p,
		const std::vector< UnivariatePolynomial< MultivariatePolynomial< Number >>> &	polynomials
	)

Implements algebraic substitution by Gröbner basis computation.

Essentially we take all polynomials and compute a Gröbner basis with respect to an elimination order, having the remaining variable at the end. The result is then the polynomial in the last variable only.

Definition at line 71 of file AlgebraicSubstitution.h.

Here is the call graph for this function:

algebraic_substitution_resultant() [1/2]

template<typename Number >

std::optional<UnivariatePolynomial<Number> > carl::ran::interval::algebraic_substitution_resultant	(	const std::vector< MultivariatePolynomial< Number >> &	polynomials,
		const std::vector< Variable > &	variables
	)

Implements algebraic substitution by resultant computation.

We iteratively compute the resultant of the input polynomial with each of the defining polynomials. Eventually we obtain a polynomial univariate in the remaining variable, our result.

Note that we assume that the polynomials are in a triangular form where any polynomial may contain variables that are `‘defined’' by the previous polynomials.

Definition at line 129 of file AlgebraicSubstitution.h.

Here is the call graph for this function:

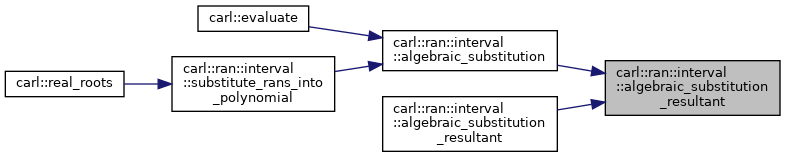
algebraic_substitution_resultant() [2/2]

template<typename Number >

std::optional<UnivariatePolynomial<Number> > carl::ran::interval::algebraic_substitution_resultant	(	const UnivariatePolynomial< MultivariatePolynomial< Number >> &	p,
		const std::vector< UnivariatePolynomial< MultivariatePolynomial< Number >>> &	polynomials
	)

Implements algebraic substitution by resultant computation.

We iteratively compute the resultant of the input polynomial with each of the defining polynomials. Eventually we obtain a polynomial univariate in the remaining variable, our result.

Note that we assume that the polynomials are in a triangular form where any polynomial may contain variables that are `‘defined’' by the previous polynomials.

Definition at line 96 of file AlgebraicSubstitution.h.

Here is the call graph for this function:

Here is the caller graph for this function:

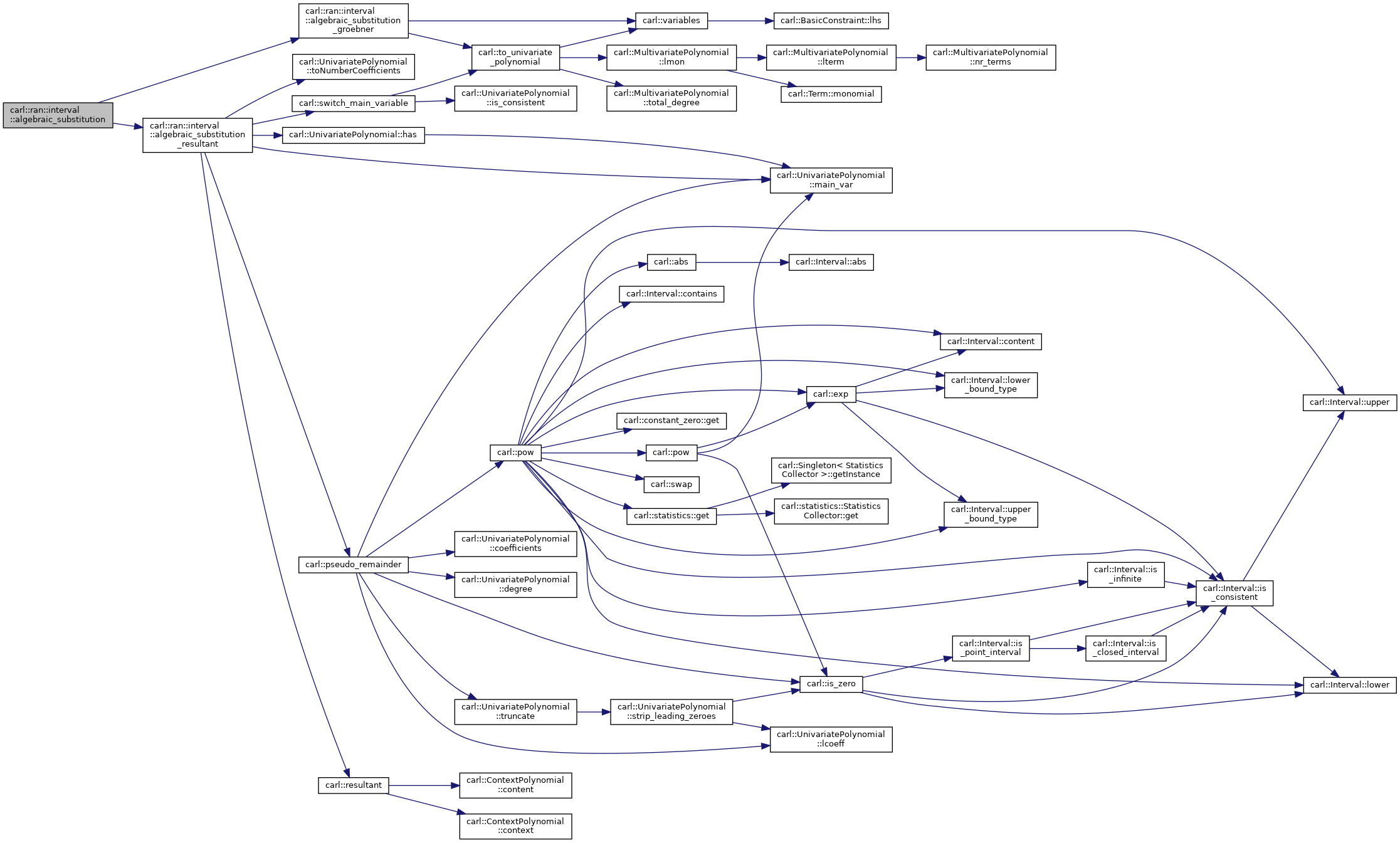
substitute_rans_into_polynomial()

template<typename Number , typename Coeff >

std::optional<UnivariatePolynomial<Number> > carl::ran::interval::substitute_rans_into_polynomial	(	const UnivariatePolynomial< Coeff > &	p,
		const OrderedAssignment< IntRepRealAlgebraicNumber< Number >> &	m,
		bool	use_lazard = false
	)

Definition at line 8 of file internal.h.

Here is the call graph for this function:

Here is the caller graph for this function: