Compact class to isolate real roots from a univariate polynomial using bisection. More...
#include <RealRootIsolation.h>

Public Member Functions | |
| RealRootIsolation (const UnivariatePolynomial< Number > &polynomial, const Interval< Number > &interval) | |
| std::vector< IntRepRealAlgebraicNumber< Number > > | get_roots () |
| Compute and sort the roots of mPolynomial within mInterval. More... | |
Private Member Functions | |
| void | eliminate_zero_roots () |
| The sturm sequence for mPolynomial. More... | |
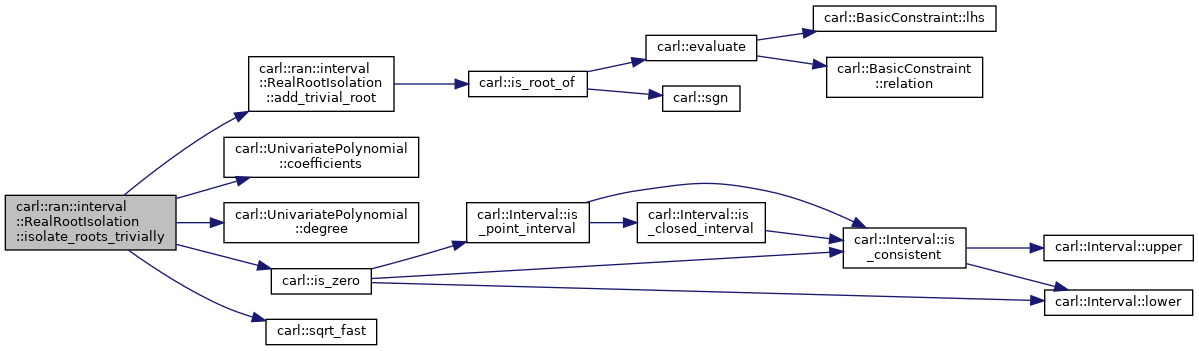
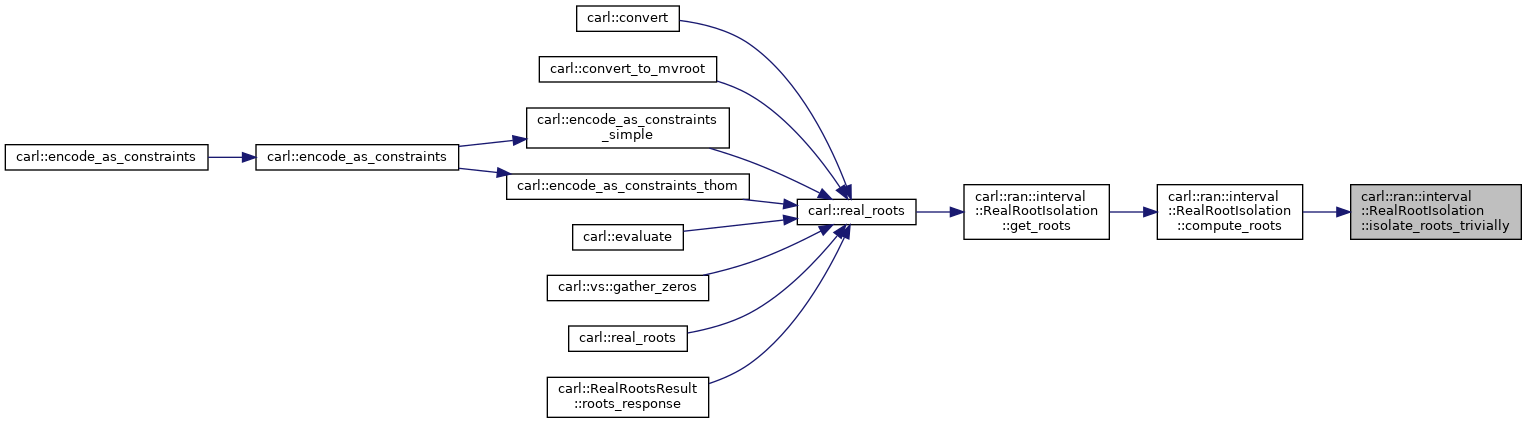
| bool | isolate_roots_trivially () |
| Directly solve low-degree polynomials. More... | |
| void | add_trivial_root (const Number &n) |
| void | add_trivial_root (const Interval< Number > &i) |
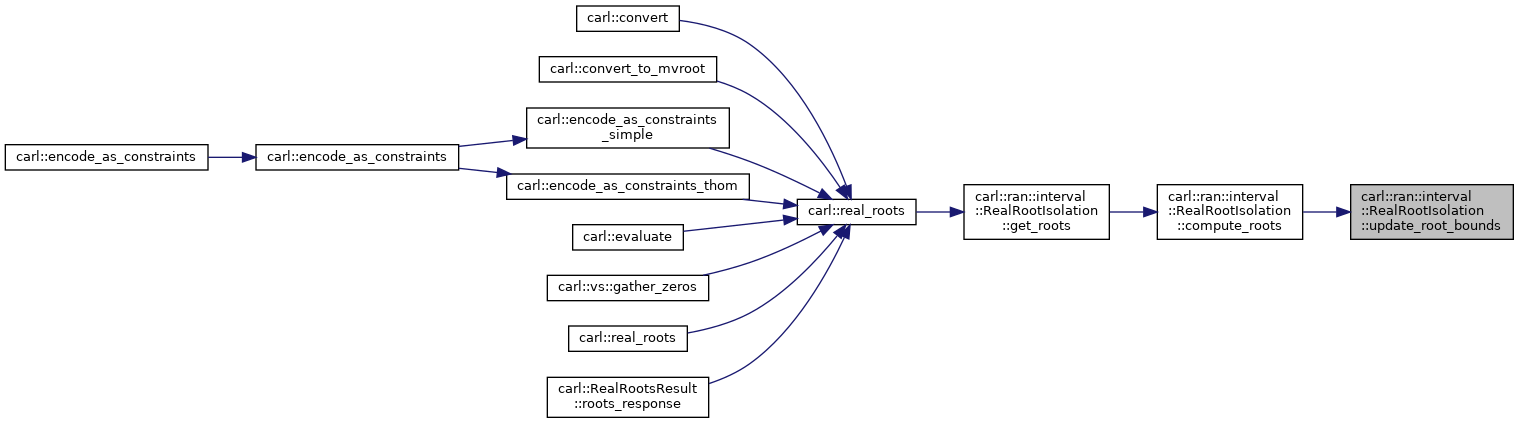
| void | update_root_bounds () |
| Use root bounds to shrink mInterval. More... | |
| void | add_root (const Number &n) |
| Add a root to mRoots and simplify polynomial accordingly (essentially divide by x-n) More... | |
| void | add_root (const Interval< Number > &i) |
| Add a root to mRoots, based on an isolating interval. More... | |
| bool | check_interval_bounds () |
| Check whether the interval bounds are roots. More... | |
| void | bisect_by_approximation (std::deque< Interval< Number >> &queue) |
| Initialize the bisection queue using approximations. More... | |
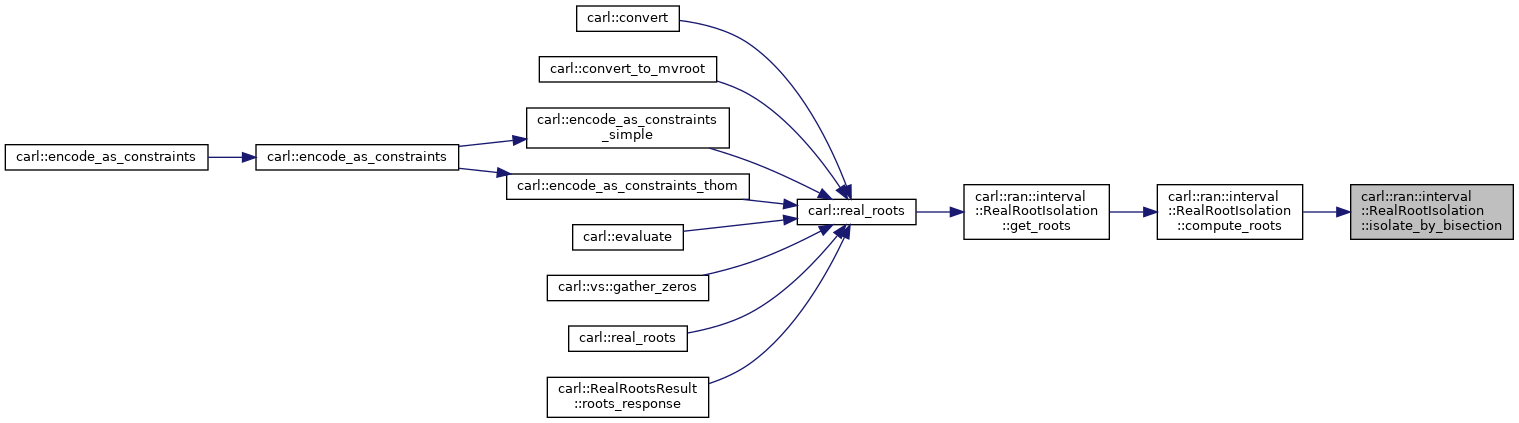
| void | isolate_by_bisection () |
| Perform bisection. More... | |
| void | compute_roots () |
| Do actual root isolation. More... | |
Private Attributes | |
| UnivariatePolynomial< Number > | mPolynomial |
| The polynomial. More... | |
| std::vector< IntRepRealAlgebraicNumber< Number > > | mRoots |
| The list of roots. More... | |
| Interval< Number > | mInterval |
| The bounding interval. More... | |
Static Private Attributes | |
| static constexpr bool | initialize_bisection_by_approximation = true |
| Initialize bisection intervals using approximations. More... | |
| static constexpr bool | simplify_by_factorization = false |
| Factorize polynomial and handle factors individually. More... | |
Detailed Description
template<typename Number>
class carl::ran::interval::RealRootIsolation< Number >
Compact class to isolate real roots from a univariate polynomial using bisection.
After some rather easy preprocessing (make polynomial square-free, eliminate zero roots, solve low-degree polynomial trivially, use root bounds to shrink the interval) we employ bisection which can optionally be initialized by approximations.
Definition at line 26 of file RealRootIsolation.h.
Constructor & Destructor Documentation
◆ RealRootIsolation()
|
inline |
Definition at line 296 of file RealRootIsolation.h.
Member Function Documentation
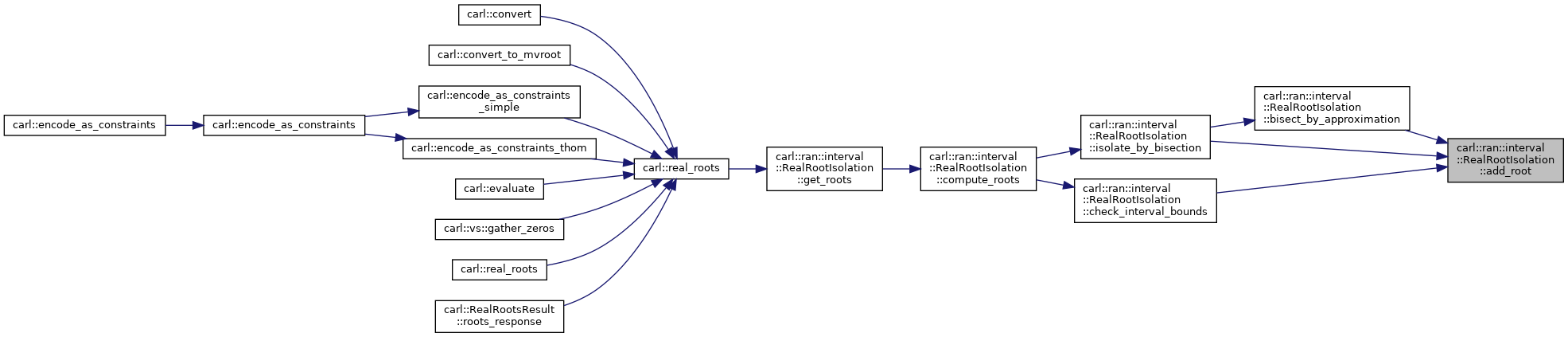
◆ add_root() [1/2]
|
inlineprivate |
Add a root to mRoots, based on an isolating interval.
Definition at line 141 of file RealRootIsolation.h.
◆ add_root() [2/2]
|
inlineprivate |
Add a root to mRoots and simplify polynomial accordingly (essentially divide by x-n)
Definition at line 133 of file RealRootIsolation.h.

◆ add_trivial_root() [1/2]
|
inlineprivate |
Definition at line 120 of file RealRootIsolation.h.
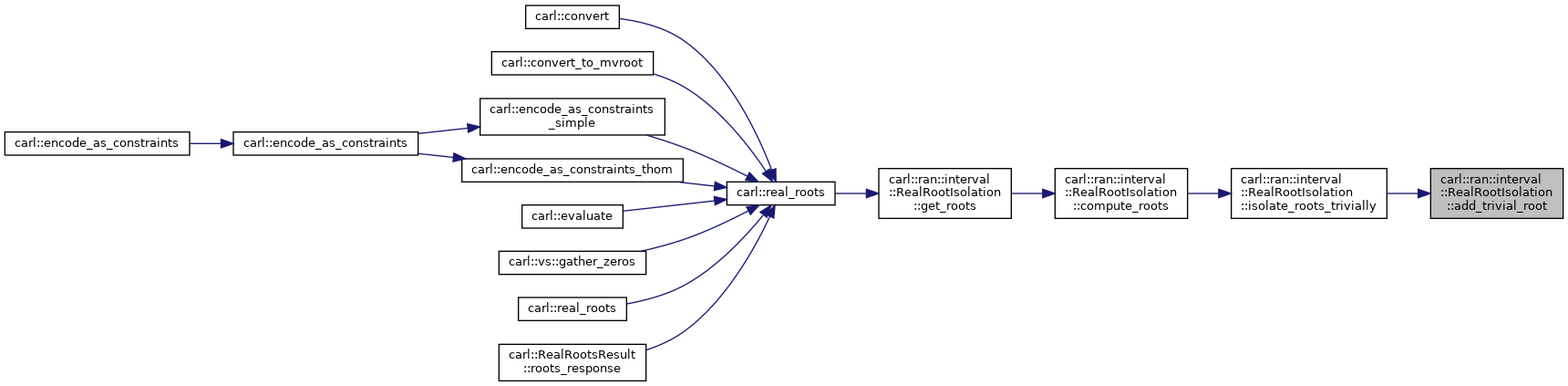
◆ add_trivial_root() [2/2]
|
inlineprivate |
Definition at line 114 of file RealRootIsolation.h.

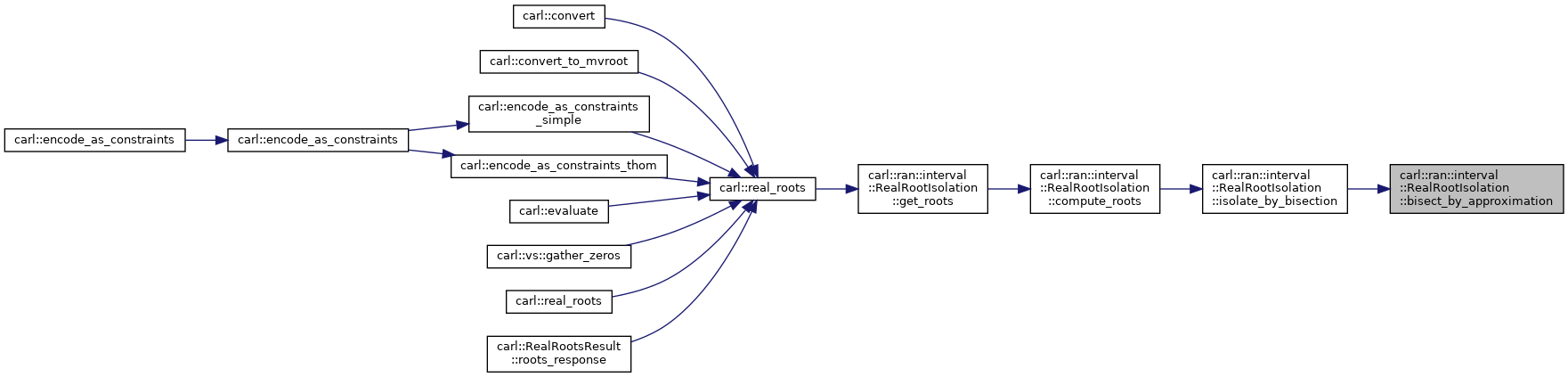
◆ bisect_by_approximation()
|
inlineprivate |
Initialize the bisection queue using approximations.
The main idea is that the eigenvalues of the companion matrix are the root of a polynomial. This is implemented in eigen::root_approximation. We do:
- convert coefficients to doubles
- call eigen::root_approximation
- make approximations smaller, sort them, remove duplicates
- convert approximations to rationals
- create interval endpoints so that each interval contains a single approximation
- initialize queue from these endpoints
Definition at line 177 of file RealRootIsolation.h.

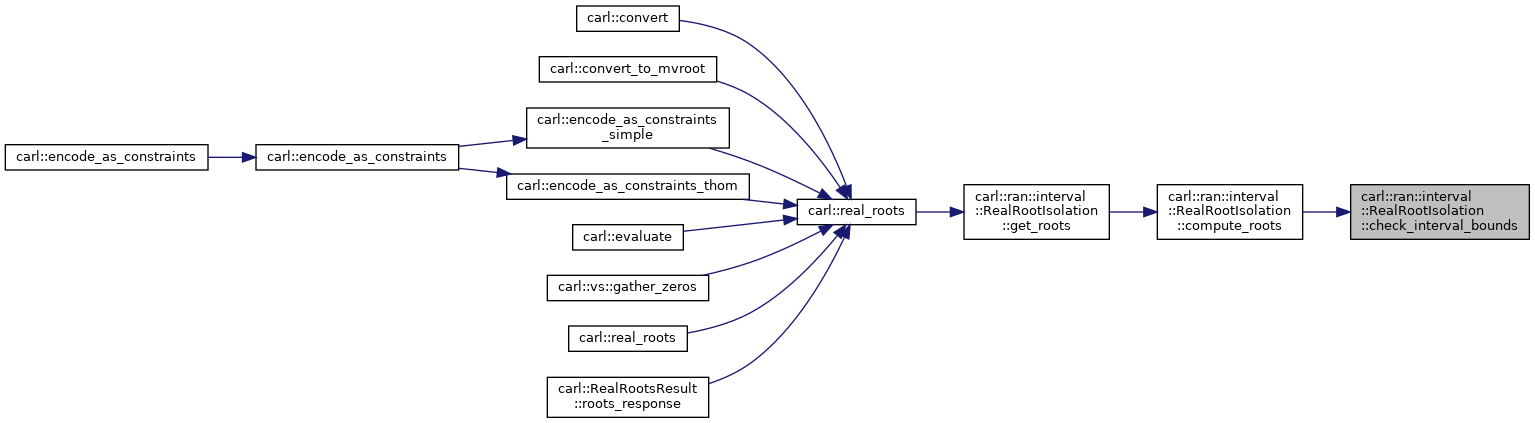
◆ check_interval_bounds()
|
inlineprivate |
Check whether the interval bounds are roots.
Definition at line 147 of file RealRootIsolation.h.

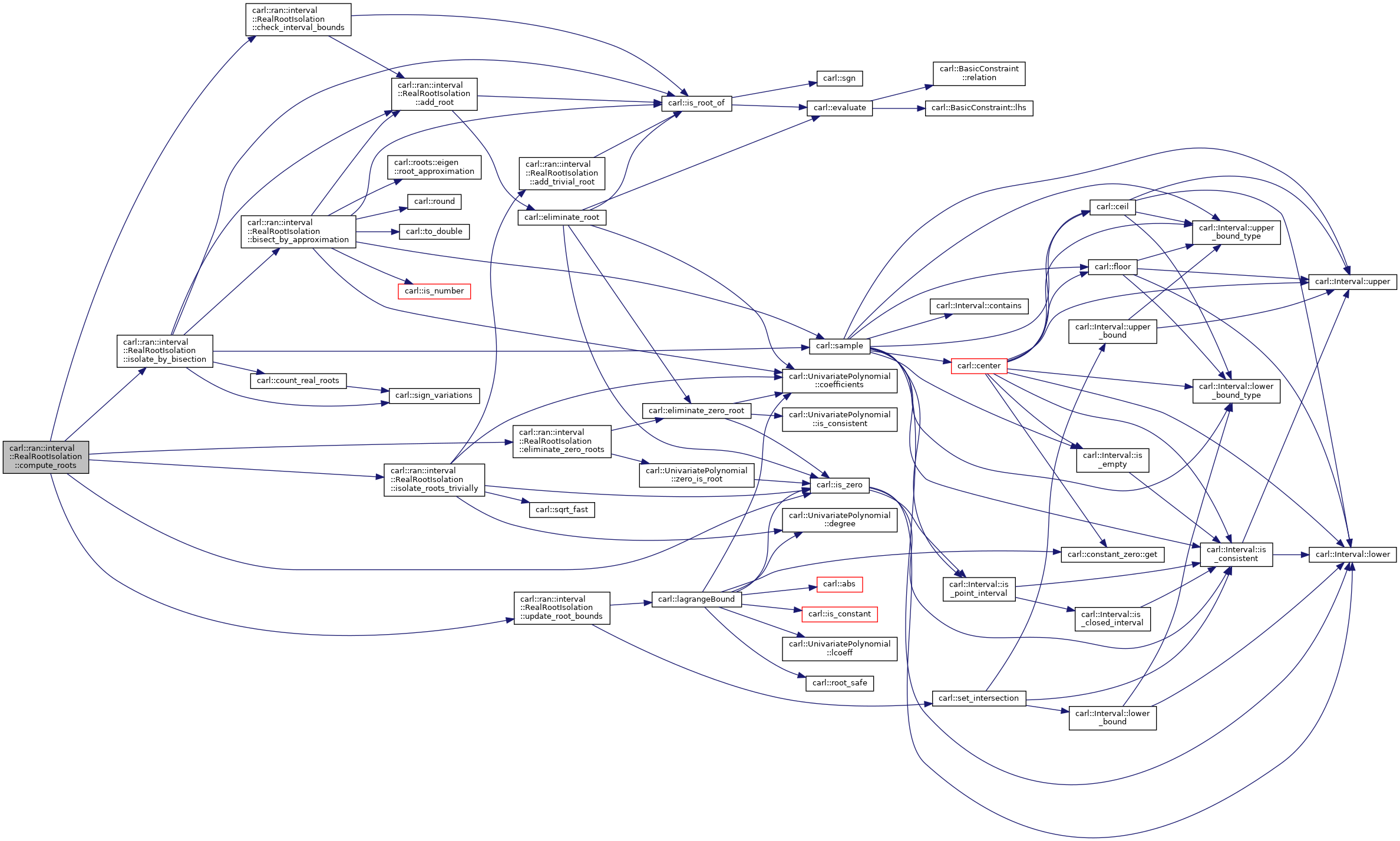
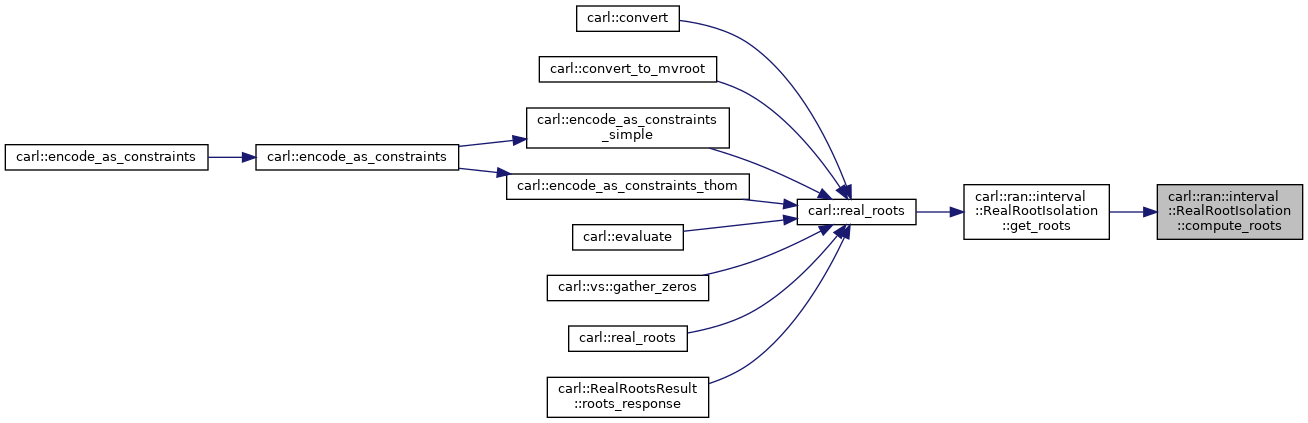
◆ compute_roots()
|
inlineprivate |
Do actual root isolation.
Definition at line 269 of file RealRootIsolation.h.
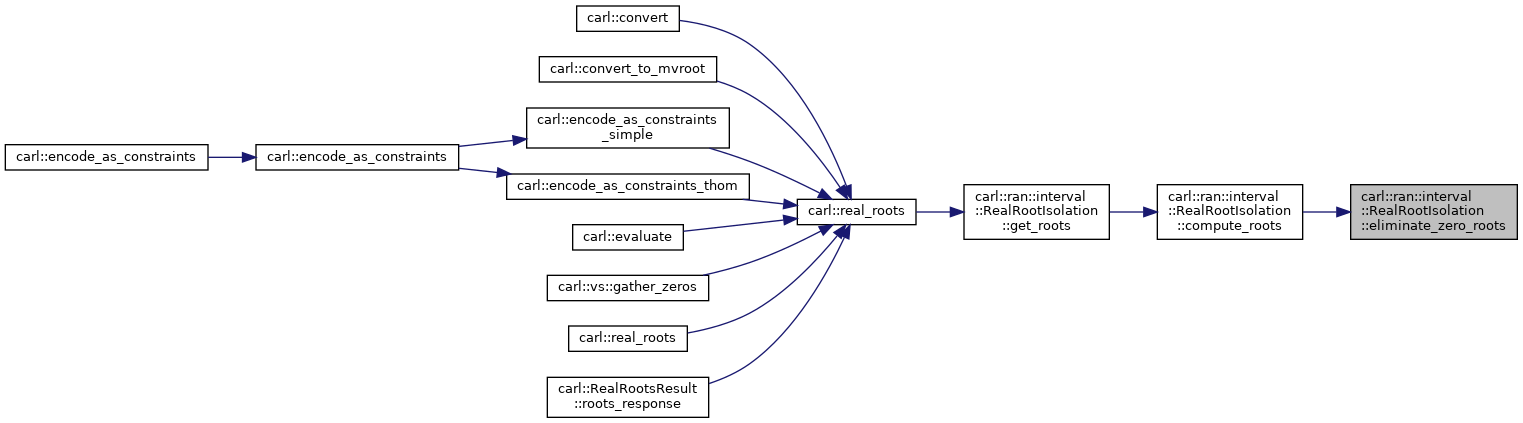
◆ eliminate_zero_roots()
|
inlineprivate |
The sturm sequence for mPolynomial.
Return the sturm sequence for mPolynomial, create it if necessary. Reset the sturm sequence, used if the polynomial was modified. Handle zero roots (p(0) == 0)
Definition at line 54 of file RealRootIsolation.h.

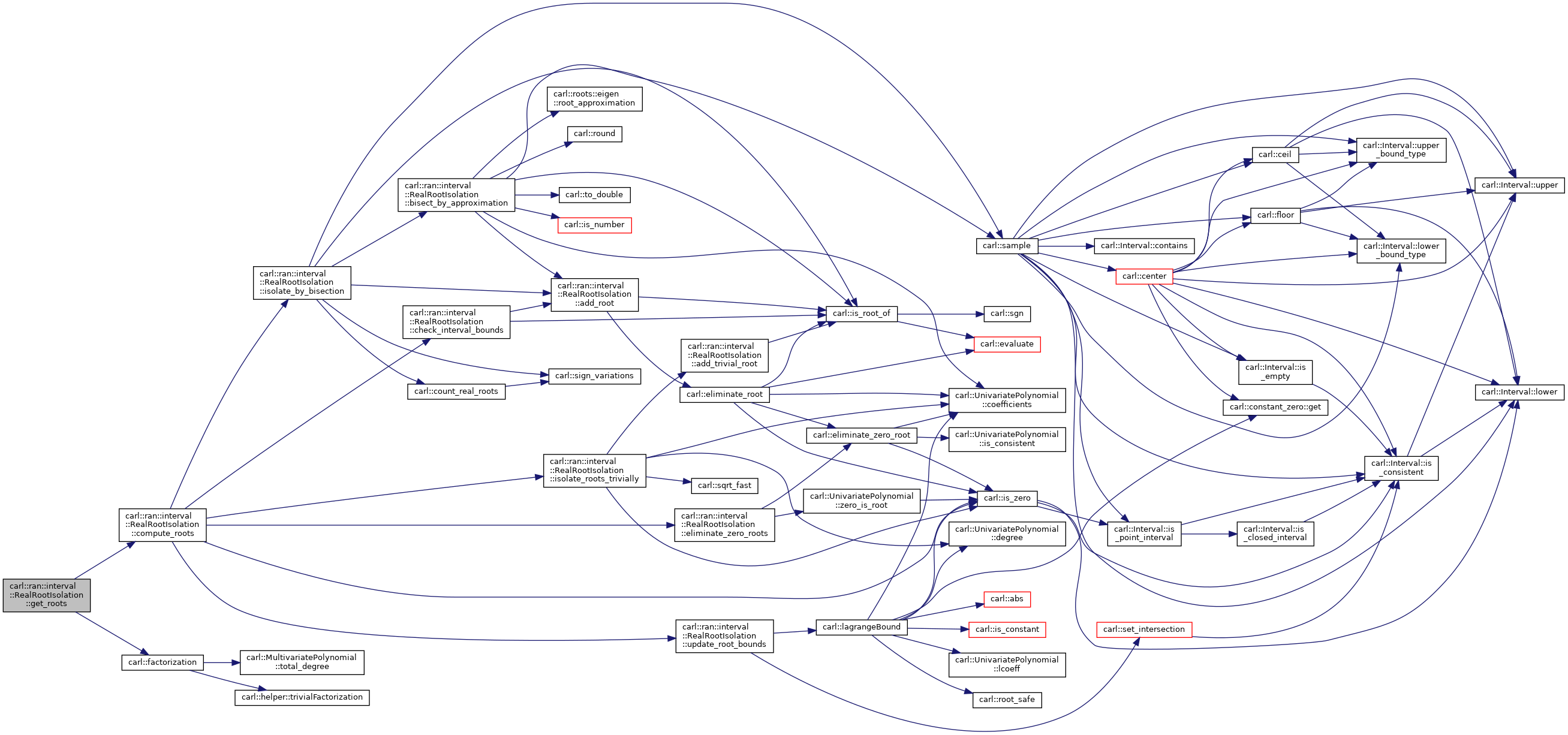
◆ get_roots()
|
inline |
Compute and sort the roots of mPolynomial within mInterval.
Definition at line 301 of file RealRootIsolation.h.

◆ isolate_by_bisection()
|
inlineprivate |
Perform bisection.
Definition at line 231 of file RealRootIsolation.h.

◆ isolate_roots_trivially()
|
inlineprivate |
Directly solve low-degree polynomials.
Definition at line 64 of file RealRootIsolation.h.
◆ update_root_bounds()
|
inlineprivate |
Use root bounds to shrink mInterval.
Definition at line 126 of file RealRootIsolation.h.

Field Documentation
◆ initialize_bisection_by_approximation
|
staticconstexprprivate |
Initialize bisection intervals using approximations.
Definition at line 28 of file RealRootIsolation.h.
◆ mInterval
|
private |
The bounding interval.
Definition at line 37 of file RealRootIsolation.h.
◆ mPolynomial
|
private |
The polynomial.
Definition at line 33 of file RealRootIsolation.h.
◆ mRoots
|
private |
The list of roots.
Definition at line 35 of file RealRootIsolation.h.
◆ simplify_by_factorization
|
staticconstexprprivate |
Factorize polynomial and handle factors individually.
Definition at line 30 of file RealRootIsolation.h.
The documentation for this class was generated from the following file:
- carl-arith/ran/interval/helper/RealRootIsolation.h