smtrat::cad::projection::mccallum Namespace Reference

Contains the implementation of McCallums projection operator as specified in [23]. More...

Functions
template<typename Poly , typename Callback >
void	single (const Poly &p, carl::Variable variable, Callback &&cb)
	Implements the part of McCallums projection operator from [23] that deals with a single polynomial p: . More...
template<typename Poly , typename Callback >
void	paired (const Poly &p, const UPoly &q, carl::Variable variable, Callback &&cb)
	Implements the part of McCallums projection operator from [23] that deals with two polynomials p and q: . More...

Detailed Description

Contains the implementation of McCallums projection operator as specified in [23].

Function Documentation

paired()

template<typename Poly , typename Callback >

void smtrat::cad::projection::mccallum::paired	(	const Poly &	p,
		const UPoly &	q,
		carl::Variable	variable,
		Callback &&	cb
	)

Implements the part of McCallums projection operator from [23] that deals with two polynomials p and q: .

Definition at line 35 of file McCallum.h.

Here is the call graph for this function:

Here is the caller graph for this function:

single()

template<typename Poly , typename Callback >

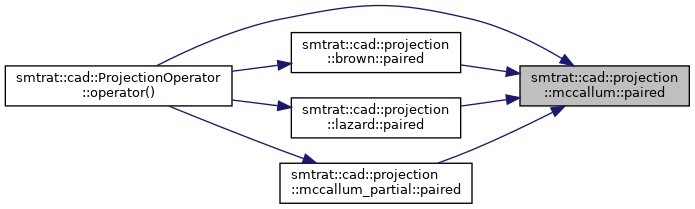
void smtrat::cad::projection::mccallum::single	(	const Poly &	p,
		carl::Variable	variable,
		Callback &&	cb
	)

Implements the part of McCallums projection operator from [23] that deals with a single polynomial p: .

Definition at line 19 of file McCallum.h.

Here is the call graph for this function:

Here is the caller graph for this function: