 |
SMT-RAT
24.02
Toolbox for Strategic and Parallel Satisfiability-Modulo-Theories Solving
|
 |
SMT-RAT
24.02
Toolbox for Strategic and Parallel Satisfiability-Modulo-Theories Solving
|
THe different parts of SMT-RAT are split into multiple libraries (in the sense of a shared object library) that are responsible for the following tasks:
smtrat-analyzer: static analysis of input formulae;smtrat-cad: back all CAD-based techniques;smtrat-common: common definitions and includes;smtrat-max-smt: takes care of max SMT queries;smtrat-mcsat: utilities for the MCSAT-based solver;smtrat-modules: all regular SMT-RAT modules;smtrat-optimization: takes care of optimization queries;smtrat-qe: methods for quantifier elimination;smtrat-solver: core solving infrastructure;smtrat-strategies: strategies for SMT solving;smtrat-unsat-cores: takes care of unsat core computations.All of these yield a library, while a full-fledged SMT solver is build from the cli/ path, in particular the cli/smtratSolver.cpp.
The architecture of SMT-RAT puts its focus on modularity and composability of different solving techniques. Every solving technique, for example SAT solving or the simplex method, is encapsulated in a (derivation of the) module class. These modules are composed to a strategy that governs which modules are used in what order. The execution of a strategy is incumbent upon the manager, that also offers an interface for basic SMT solving to the outside.
More advanced solving techniques like quantifier elimination, computing unsatisfiable cores, or tackling max SMT and optimization queries are implemented as individual components in the frontend. The frontend implements (most of) an SMT-LIB compatible interface and can either be used by a generic SMT-LIB parser, or an external tool. This structure is shown in the following picture.
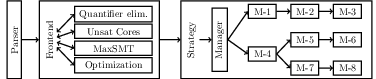
The parser itself is implemented in cli/parser/ and run from cli/tools/execute_smtlib.h. The template argument Executor is usually instantiated with the executor from cli/tools/Executor.h which corresponds to the frontend. The components in the frontend are taken from the respective SMT-RAT libraries.
The manager is a generic class from smtrat-solver/Manager.h that every strategy (from smtrat-strategies/) inherits from and only constructs the strategy graph in its constructor. The strategy graph is at the core of the composition of SMT-RAT modules and the following picture shows how a single module is embedded in a strategy.
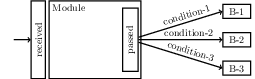
Every module has (a pointer to) a set of received formulae that represent its input and a set of passed formulae that represent the formula that is passed on to some backend. The module may "solve" the query from its input on its own, or it may pass (one or more) queries to its backends (in this case B-1, B-2 and B-3). Arrows to backends may be labeled with conditions that restrict whether this particular backend can be used, for example checking whether the passed formulae are linear, contain integer variables or bit-vector formulae.
When a module issues a backend call the manager identifies all suitable backend modules (where the condition evaluates to true) and calls all backend modules on the passed formulae. This happens either sequentially (until one backend module solves the query) or in parallel.
A module ![]() holds a set of formulas, called its set of received formulas and denoted by
holds a set of formulas, called its set of received formulas and denoted by ![]() . The main function of a module is
. The main function of a module is check(bool full), which either decides whether ![]() is satisfiable or not, returning
is satisfiable or not, returning SAT or UNSAT, respectively, or returns UNKNOWN. A set of formulas is semantically defined by their conjunction. If the function's argument full is set to false, the underlying procedure of ![]() is allowed to omit hard obstacles during solving at the cost of returning
is allowed to omit hard obstacles during solving at the cost of returning UNKNOWN in more cases. We can manipulate ![]() by adding (removing) formulas
by adding (removing) formulas ![]() to (from) it with
to (from) it with add(\f$\varphi\f$) (remove(\f$\varphi\f$)). Usually, ![]() is only slightly changed between two consecutive
is only slightly changed between two consecutive check calls, hence, the solver's performance can be significantly improved if a module works incrementally and supports backtracking. In case ![]() determines the unsatisfiability of
determines the unsatisfiability of ![]() , it has to compute at least one preferably small infeasible subset
, it has to compute at least one preferably small infeasible subset ![]() . Moreover, a module can specify lemmas, which are valid formulas. They encapsulate information which can be extracted from a module's internal state and propagated among other modules. Furthermore, a module itself can ask other modules for the satisfiability of its set of passed formulas denoted by
. Moreover, a module can specify lemmas, which are valid formulas. They encapsulate information which can be extracted from a module's internal state and propagated among other modules. Furthermore, a module itself can ask other modules for the satisfiability of its set of passed formulas denoted by ![]() , if it invokes the procedure
, if it invokes the procedure runBackends(bool full) (controlled by the manager). It thereby delegates work to modules that may be more suitable for the problem at hand.
SMT-RAT allows a user to decide how to compose the modules. For this purpose we provide a graphical user interface, where the user can create a strategy specifying this composition. A strategy is a directed tree ![]() with a set
with a set ![]() of modules as nodes and
of modules as nodes and ![]() , with
, with ![]() being the set of conditions and
being the set of conditions and ![]() being the set of priority values. A condition is an arbitrary Boolean combination of formula properties, such as propositions about the Boolean structure of the formula, e.g., whether it is in conjunctive normal form (CNF), about the constraints, \eg whether it contains equations, or about the polynomials, e.g., whether they are linear. Furthermore, each edge carries a unique priority value from
being the set of priority values. A condition is an arbitrary Boolean combination of formula properties, such as propositions about the Boolean structure of the formula, e.g., whether it is in conjunctive normal form (CNF), about the constraints, \eg whether it contains equations, or about the polynomials, e.g., whether they are linear. Furthermore, each edge carries a unique priority value from ![]() .
.
The manager holds the strategy and the SMT solver's input formula ![]() . Initially, the manager calls the method
. Initially, the manager calls the method check of the module ![]() given by the root of the strategy with
given by the root of the strategy with ![]() . Whenever a module
. Whenever a module ![]() calls
calls runBackends, the manager adds a solving task ![]() to its priority queue
to its priority queue ![]() of solving tasks (ordered by the priority value), if there exists an edge
of solving tasks (ordered by the priority value), if there exists an edge ![]() in the strategy such that
in the strategy such that ![]() holds for
holds for ![]() . If a processor
. If a processor ![]() on the machine where SMT-RAT is executed on is available, the first solving task of
on the machine where SMT-RAT is executed on is available, the first solving task of ![]() is assigned to
is assigned to ![]() and popped from
and popped from ![]() . The manager thereby starts the method
. The manager thereby starts the method check of ![]() with
with ![]() and passes the result (including infeasible subsets and lemmas) back to
and passes the result (including infeasible subsets and lemmas) back to ![]() . The module
. The module ![]() can now benefit in its solving and reasoning process from this shared information. Note that a strategy-based composition of modules works incrementally and supports backtracking not just within one module but as a whole. This is realized by a mapping in each module
can now benefit in its solving and reasoning process from this shared information. Note that a strategy-based composition of modules works incrementally and supports backtracking not just within one module but as a whole. This is realized by a mapping in each module ![]() of its passed formulas
of its passed formulas ![]() to sets
to sets ![]() such that each
such that each ![]() forms a reason why
forms a reason why ![]() included
included ![]() in
in ![]() to ask for its satisfiability. In order to exploit the incrementality of the modules, all parallel executed backends terminate in a consistent state (instead of just being killed), if one of them finds an answer.
to ask for its satisfiability. In order to exploit the incrementality of the modules, all parallel executed backends terminate in a consistent state (instead of just being killed), if one of them finds an answer.
The heart of an SMT solver usually forms a SAT solver. In SMT-RAT, the module SATModule abstracts the received formulae to propositional logic and uses the efficient SAT solver MiniSat [minisat] to find a Boolean assignment of the abstraction. It invokes runBackends where the passed formulae of the SATModule contain the constraints abstracted by the assigned Boolean variables in a less-lazy fashion [sebastiani2007lazy]. [Todo: Make a concise description here, refer to extensive discussion of modules]
Infeasible subsets and lemmas, which contain only formulas from ![]() of a preceding SATModule, prune its Boolean search space and hence the number of theory calls. Smaller infeasible subsets are usually more advantageous, because they make larger cuts in the search space. We call lemmas containing new constraints inventive lemmas (non-inventive otherwise). They might enlarge the Boolean search space, but they can reduce the complexity of later theory calls. When using inventive lemmas, it is important to ensure that the set possible constraints introduced in such lemmas is finite for a given module and a given input formula. Otherwise, the termination of this procedure cannot be guaranteed. In general, any module might contribute lemmas and all preceding modules in the solving hierarchy can directly involve them in their search for satisfiability.
of a preceding SATModule, prune its Boolean search space and hence the number of theory calls. Smaller infeasible subsets are usually more advantageous, because they make larger cuts in the search space. We call lemmas containing new constraints inventive lemmas (non-inventive otherwise). They might enlarge the Boolean search space, but they can reduce the complexity of later theory calls. When using inventive lemmas, it is important to ensure that the set possible constraints introduced in such lemmas is finite for a given module and a given input formula. Otherwise, the termination of this procedure cannot be guaranteed. In general, any module might contribute lemmas and all preceding modules in the solving hierarchy can directly involve them in their search for satisfiability.